贵州省铜仁市石阡县2020-2021学年七年级上学期数学期末考试试卷

试卷更新日期：2021-03-24 类型：期末考试

进入出卷网下载

一、单选题

1. $- 2$ 的相反数是（）

A、 $- 2$ B、2 C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
2. 已知 $∠ α = 35 °$ ，则 $∠ α$ 的余角是（）

A、 $55 °$ B、 $65 °$ C、 $145 °$ D、 $165 °$

查看试题解析
3. 下列各式中与多项式 $a - b - c$ 不相等的是（）

A、 $a - (b + c)$ B、 $a - (b - c)$ C、 $(a - b) + (- c)$ D、 $- b - (c - a)$

查看试题解析
4. 如果 $\frac{1}{3} x^{a + 1} y^{2 a + 3}$ 与 $- 3 x^{2} y^{2 b - 1}$ 是同类项，那么a，b的值分别是（）

A、 $a = 1$ ， $b = 2$ B、 $a = 1$ ， $b = 3$ C、 $a = 2$ ， $b = 3$ D、 $a = 3$ ， $b = 2$

查看试题解析
5. 地球绕太阳转动（即地球的公转）每小时转过11万千米，用科学记数法表示为（）

A、 $11 \times 10^{4}$ 千米 B、 $1.1 \times 10^{4}$ 千米 C、 $1.1 \times 10^{5}$ 千米 D、 $11 \times 10^{5}$ 千米

查看试题解析
6. 一件上衣标价为600元，按8折销售可获利20元.设这件上衣的成本价为x元.根据题意，可得方程（）

A、600×0.8-x=20 B、600×8-x=20 C、600×0.8=x-20 D、600×8=x-20

查看试题解析
7. 下列说法：①两点确定一条直线；②两点之间，线段最短；③若 $A B = B C$ ，则点B是线段 $A C$ 的中点；④若 $∠ 1 + ∠ 2 = 180 °$ ，则 $∠ 1$ 与 $∠ 2$ 互为补角；⑤连接两点之间的线段叫两点间的距离.其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 某汽车站为了了解某月每天上午乘车人数，抽查了其中10天的每天上午的乘车人数，所抽查的这10天每天上午乘车人数是这个问题的 ( )

A、一个样本 B、一个个体 C、样本容量 D、一个总体

查看试题解析
9. 已知关于x的方程2x+a-9=0的解是x=2，则a的值为

A、2 B、3 C、4 D、5

查看试题解析
10. 下列图形都是由同样大小的小圆圈按一定规律所组成的，其中第①个图形中一共有6个小圆圈，第②个图形中一共有9个小圆圈，第③个图形中一共有12个小圆圈，…，按此规律排列，则第⑦个图形中小圆圈的个数为（）

A、21 B、24 C、27 D、30

查看试题解析

二、填空题

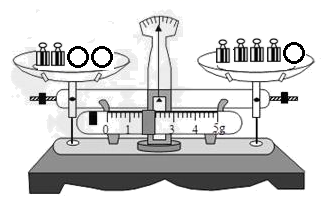
11. 在数轴上，表示 $- 2020$ 的点与原点的距离是.

查看试题解析
12. 按下面程序计算：输入 $x \to$ 立方 $\to - x \to \div 2 \to$ 答案输入 $x = - 3$ ，则输出的答案是.

查看试题解析
13. 如图，天平托盘中每个小球的质量用 $x g$ 表示，砝码每个 $10 g$ ，那么 $x =$ .

查看试题解析
14. 延长线段 $A B$ 到C，使 $B C = \frac{1}{3} A B$ ，D为 $A C$ 的中点，且 $D C = 6 cm$ ，则 $A B$ 的长为.

查看试题解析
15. 一根长为5a＋4b的铁丝，剪下一部分围成一个长为a、宽为b的长方形，则这根铁丝还剩下．

查看试题解析
16. 如图，把长方形的一角折叠，得到折痕 $E F$ ，已知 $∠ E F B = 35 °$ ，则 $∠ B F C =$ 度.

查看试题解析
17. 若规定一种运算“ $※$ ”： $a ※ b = a + a^{b}$ ，则 $1 ※ (2 ※ 3) =$ .

查看试题解析
18. 已知方程x-2=2x+1的解也是关于x的方程k(x-2)= $\frac{x + 1}{2}$ ，则k的值是。

查看试题解析

三、解答题

19. 计算或解方程：

(1)、 $5 \times {(- 3)}^{2} + 6 \div (- 2) \times | \frac{1}{3} - 1 |$

(2)、 $- 1 - (1 - 0.5) \times \frac{1}{3} \times [2 - {(- 3)}^{2}]$

(3)、 $3 x - 2 (10 - x) = 5$

(4)、 $\frac{x}{0.3} = 1 + \frac{1.2 - 0.3 x}{0.2}$

查看试题解析
20. 先化简，再求值： $2 x - [2 (x + 4) - 3 (x + 2 y)] - 2 y$ ，其中 $| x + 1 | + {(y - 2)}^{2} = 0$ .

查看试题解析
21. 如图，已知线段 $A B$ 和 $C D$ 的公共部分 $B D = \frac{1}{3} A B = \frac{1}{4} C D$ ，线段 $A B$ 、 $C D$ 的中点E、F之间的间距是 $10 cm$ ，求 $A B$ 、 $C D$ 的长.

查看试题解析
22. “低碳生活，绿色出行”是我们倡导的一种生活方式，有关部门抽样调查了某单位员工上下班的交通方式，绘制了两幅统计图：

(1)、样本中的总人数为人；扇形统计十图中“骑自行车”所在扇形的圆心角为度；

(2)、补全条形统计图；

(3)、该单位共有1000人，积极践行这种生活方式，越来越多的人上下班由开私家车改为骑自行车.若步行，坐公交车上下班的人数保持不变，问原来开私家车的人中至少有多少人改为骑自行车，才能使骑自行车的人数不低于开私家车的人数？

查看试题解析
23. 文具店销售某种笔袋，每个18元，小华去购买这种笔袋，结账时店员说：“如果你再多买一个就可以打九折，价钱比现在便宜36元”小华说：“那就多买一个吧，谢谢.”根据两人的对话可知，小华结账时实际买了多少个笔袋？

查看试题解析
24. 如图， $∠ A O B = 90 °$ ， $O E$ 是 $∠ A O C$ 的平分线， $O D$ 是 $∠ B O C$ 的平分线，若 $∠ B O C = 30 °$ .

(1)、求 $∠ D O E$ 的度数；

(2)、若没有给出 $∠ B O C$ 的度数，你能否求出 $∠ D O E$ 的度数？请说明理由；

(3)、在（2）的条件下，若 $∠ A O B = α$ ，求 $∠ D O E$ 的度数，你能从中发现什么规律？

查看试题解析