广东省潮州市潮安区2019-2020学年七年级下学期数学期中试卷
试卷更新日期:2021-03-23 类型:期中考试
一、单选题
-
1. 4的平方根是( )A、2 B、–2 C、±2 D、±2. 下列图形中,哪个可以通过图1平移得到( )
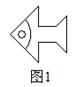 A、
A、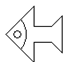 B、
B、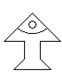 C、
C、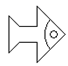 D、
D、 3. 在下列实数: 、 、 、 、﹣1.010010001…中,无理数有( )A、1个 B、2个 C、3个 D、4个4. 在平面直角坐标系中,点(-3,-2)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 如果 是a 的相反数,那么a的值是( )A、 B、 C、 D、6. 如图,直线AB,CD相交于点O,若∠1+∠2=100°,则∠BOC等于( )
3. 在下列实数: 、 、 、 、﹣1.010010001…中,无理数有( )A、1个 B、2个 C、3个 D、4个4. 在平面直角坐标系中,点(-3,-2)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 如果 是a 的相反数,那么a的值是( )A、 B、 C、 D、6. 如图,直线AB,CD相交于点O,若∠1+∠2=100°,则∠BOC等于( ) A、130° B、140° C、150° D、160°7. 如图,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )
A、130° B、140° C、150° D、160°7. 如图,点E在AC的延长线上,下列条件中能判断AB∥CD的是( )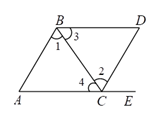 A、∠3=∠4 B、∠1=∠2 C、∠D=∠DCE D、∠D+∠DCA=180°8. 下列命题中正确的有( )
A、∠3=∠4 B、∠1=∠2 C、∠D=∠DCE D、∠D+∠DCA=180°8. 下列命题中正确的有( )①相等的角是对顶角; ②在同一平面内,若a∥b,b∥c,则a∥c;
③同旁内角互补; ④互为邻补角的两角的角平分线互相垂直.
A、4个 B、1个 C、2个 D、3个9. 已知点M(a,b)在第三象限,则点N(﹣b,a)在第( )象限.A、一 B、二 C、三 D、四10. 如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为( )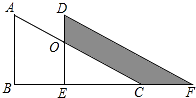 A、48 B、96 C、84 D、42
A、48 B、96 C、84 D、42二、填空题
-
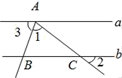
11. 化简: = .12. 已知点P在第四象限,且到x轴的距离是3,到y轴的距离是2,则点P的坐标为 .13. 如图,已知a∥b,∠1=70°,∠2=40°,则∠3=度.
 14. 如图,直线AB , CD相交于点O , OA平分∠EOC , ∠EOD=120°,则∠BOD=°.
14. 如图,直线AB , CD相交于点O , OA平分∠EOC , ∠EOD=120°,则∠BOD=°.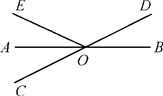 15. 若 ,且a,b是两个连续的整数,则a+b的值为16. 已知点 、 ,点P在 轴上,且 的面积为5,则点P的坐标为.17. 如图,已知A1(1,0),A2(1,﹣1),A3(﹣1,﹣1),A4(﹣1,1),A5(2,1),…则点A2020的坐标是 .
15. 若 ,且a,b是两个连续的整数,则a+b的值为16. 已知点 、 ,点P在 轴上,且 的面积为5,则点P的坐标为.17. 如图,已知A1(1,0),A2(1,﹣1),A3(﹣1,﹣1),A4(﹣1,1),A5(2,1),…则点A2020的坐标是 .
三、解答题
-
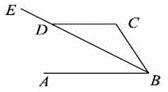
18. 计算: .19. 如图,AB∥CD,BE平分∠ABC,∠DCB=140°,求∠ABD和∠EDC的度数.
 20. 有一个边长为9 cm的正方形和一个长为24 cm、宽为6 cm的长方形,要作一个面积为这两个图形的面积之和的正方形,问边长应为多少厘米?
20. 有一个边长为9 cm的正方形和一个长为24 cm、宽为6 cm的长方形,要作一个面积为这两个图形的面积之和的正方形,问边长应为多少厘米?
21. 完成下面的证明过程:如图所示,

直线AD与AB,CD分别相交于点A,D,与EC,BF分别相交于点H,G,已知∠1=∠2,∠B=∠C.
求证:∠A=∠D.
证明:∵∠1=∠2,(已知)∠2=∠AGB()
∴∠1=
∴EC∥BF()
∴∠B=∠AEC()
又∵∠B=∠C(已知)
∴∠AEC=()
∴()
∴∠A=∠D()
22. 如图,AD⊥BC于点D,EG⊥BC于点G,∠E=∠3,证明:AD平分∠BAC. 23. 如图,三角形ABO中,A(﹣2,﹣3)、B(2,﹣1),三角形A′B′O′是三角形ABO平移之后得到的图形,并且O的对应点O′的坐标为(4,3).
23. 如图,三角形ABO中,A(﹣2,﹣3)、B(2,﹣1),三角形A′B′O′是三角形ABO平移之后得到的图形,并且O的对应点O′的坐标为(4,3). (1)、求三角形ABO的面积;(2)、作出三角形ABO平移之后的图形三角形A′B′O′,并写出A′、B′两点的坐标分别为A′、B′;(3)、P(x,y)为三角形ABO中任意一点,则平移后对应点P′的坐标为 .24. 如图,在直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式
(1)、求三角形ABO的面积;(2)、作出三角形ABO平移之后的图形三角形A′B′O′,并写出A′、B′两点的坐标分别为A′、B′;(3)、P(x,y)为三角形ABO中任意一点,则平移后对应点P′的坐标为 .24. 如图,在直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式 (1)、求a、b、c的值;(2)、如果在第二象限内有一点P(m, ),请用含m的式子表示四边形ABOP的面积;(3)、在(2)的条件下,是否存在点P,使四边形ABOP的面积为△ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.25. 同一平面内的两条直线有相交和平行两种位置关系.
(1)、求a、b、c的值;(2)、如果在第二象限内有一点P(m, ),请用含m的式子表示四边形ABOP的面积;(3)、在(2)的条件下,是否存在点P,使四边形ABOP的面积为△ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.25. 同一平面内的两条直线有相交和平行两种位置关系. (1)、如图1,若AB∥CD,点P在AB、CD内部,请写出∠BPD、∠B、∠D之间的数量关系(不必说明理由);(2)、如图2,将直线AB绕点B逆时针方向转一定角度交直线CD于点Q,利用(1)中的结论求∠BPD、∠B、∠D、∠BQD之间有何数量关系?并证明你的结论;(3)、如图3,设BF交AC于点M,AE交DF于点N.已知∠AMB=140°,∠ANF=105°,利用(2)中的结论直接写出∠B+∠E+∠F的度数和∠A比∠F大多少度.
(1)、如图1,若AB∥CD,点P在AB、CD内部,请写出∠BPD、∠B、∠D之间的数量关系(不必说明理由);(2)、如图2,将直线AB绕点B逆时针方向转一定角度交直线CD于点Q,利用(1)中的结论求∠BPD、∠B、∠D、∠BQD之间有何数量关系?并证明你的结论;(3)、如图3,设BF交AC于点M,AE交DF于点N.已知∠AMB=140°,∠ANF=105°,利用(2)中的结论直接写出∠B+∠E+∠F的度数和∠A比∠F大多少度.