黑龙江省佳木斯市桦南县2019-2020学年八年级下学期数学期中试卷
试卷更新日期:2021-03-23 类型:期中考试
一、单选题
-
1. 下列计算结果正确的是( )A、 B、 C、 D、2. 下列二次根式中,不能与 合并的是( )A、 B、 C、 D、3. 如图,x轴、y轴上分别有两点A(3,0)、B(0,2),以点A为圆心,AB为半径的弧交x轴负半轴于点C,则点C的坐标为( )
 A、(﹣1,0) B、(2﹣ ,0) C、(1+ ,0) D、(3- ,0)4. 校园内有两棵树,相距12米,一棵树高为13米,另一棵树高8米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞( )A、10米 B、11米 C、12米 D、13米5. 下列各组条件中,不能判定四边形 是平行四边形的是( )A、 , B、 , C、 , D、 ,6. 矩形、菱形、正方形都具有的性质是( )A、对角线相等 B、对角线互相平分 C、对角线互相垂直 D、对角线互相平分且相等7. 若一直角三角形的两边为5和12,则它第三边的长为( )A、13 B、 C、13或 D、13或8. 如图,正方形ABCD的边长为4,点E在边AB上,AE=1,若点P为对角线BD上的一个动点,则△PAE周长的最小值是( )
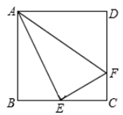
A、(﹣1,0) B、(2﹣ ,0) C、(1+ ,0) D、(3- ,0)4. 校园内有两棵树,相距12米,一棵树高为13米,另一棵树高8米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞( )A、10米 B、11米 C、12米 D、13米5. 下列各组条件中,不能判定四边形 是平行四边形的是( )A、 , B、 , C、 , D、 ,6. 矩形、菱形、正方形都具有的性质是( )A、对角线相等 B、对角线互相平分 C、对角线互相垂直 D、对角线互相平分且相等7. 若一直角三角形的两边为5和12,则它第三边的长为( )A、13 B、 C、13或 D、13或8. 如图,正方形ABCD的边长为4,点E在边AB上,AE=1,若点P为对角线BD上的一个动点,则△PAE周长的最小值是( ) A、3 B、4 C、5 D、69. 如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点B落在点B′处,则重叠部分△AFC的面积为( )
A、3 B、4 C、5 D、69. 如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点B落在点B′处,则重叠部分△AFC的面积为( ) A、12 B、10 C、8 D、610. 如图,四边形ABCD是平行四边形,点E是边CD上一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC.其中正确结论的个数为( )
A、12 B、10 C、8 D、610. 如图,四边形ABCD是平行四边形,点E是边CD上一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC.其中正确结论的个数为( )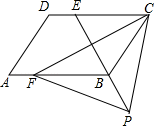 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 要使 有意义,则x可以取的最小整数是 .12. 若y= + ﹣3,则x+y= .13. 已知x+y=﹣5,xy=4,则 + = .14. 下列命题中逆命题成立的有(填序号).
①同旁内角互补,两直线平行;
②如果两个角是直角,那么它们相等;
③全等三角形的对应边相等;
④如果两个实数相等,那么它们的平方相等.
15.如图,在正方形ABCD的外侧,作等边△ADE,则∠AEB= .
 16. 如图,四边形ABCD是菱形,AC=16,DB=12,DH⊥AB于点H,则DH等于 .
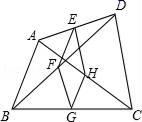
16. 如图,四边形ABCD是菱形,AC=16,DB=12,DH⊥AB于点H,则DH等于 .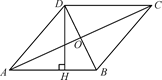 17. 如图,△ABC中,BD平分∠ABC,且AD⊥BD,E为AC的中点,AD=6cm,BD=8Cm,BC=16cm,则DE的长为.
17. 如图,△ABC中,BD平分∠ABC,且AD⊥BD,E为AC的中点,AD=6cm,BD=8Cm,BC=16cm,则DE的长为. 18. 如图,菱形ABCD的面积为120cm2 , 正方形AECF的面积为50cm2 , 则菱形的边长为cm.
18. 如图,菱形ABCD的面积为120cm2 , 正方形AECF的面积为50cm2 , 则菱形的边长为cm. 19. 如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为 .
19. 如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为 . 20. 如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A,C的坐标分别为A(10,0),C(0,4),点D是OA的中点,点P为线段BC上的点.小明同学写出了一个以OD为腰的等腰三角形ODP的顶点P的坐标(3,4),请你写出其余所有符合这个条件的P点坐标 .
20. 如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A,C的坐标分别为A(10,0),C(0,4),点D是OA的中点,点P为线段BC上的点.小明同学写出了一个以OD为腰的等腰三角形ODP的顶点P的坐标(3,4),请你写出其余所有符合这个条件的P点坐标 .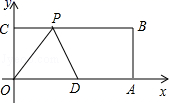
三、解答题
-
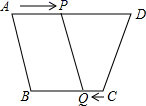
21. 在四边形ABCD中,AD∥BC,且AD>BC,BC=6cm,P、Q分别从A、C同时出发,P以1cm/s的速度由A向D运动,Q以2cm/s的速度由C出发向B运动,几秒后四边形ABQP是平行四边形?