广东省英德市2019-2020学年八年级下学期数学期中试卷

试卷更新日期：2021-03-23 类型：期中考试

进入出卷网下载

一、单选题

1. “ $x$ 与 $6$ 的差大于 $3$ ”列出的不等式符合题意是（）

A、 $x - 6 \geq 3$ B、 $x - 6 \leq 3$ C、 $x - 6 > 3$ D、 $x - 6 < 3$

查看试题解析
2. 下列图形中既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
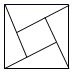3. 若 $a > b$ ，则下列不等式正确的是（）

A、 $a + 1 < b + 1$ B、 $a - 3 > b - 3$ C、 $2 a < 2 b$ D、 $\frac{a}{4} < \frac{b}{4}$

查看试题解析
4. 把不等式x+1≥0的解集在数轴上表示出来，则正确的是（）

A、 B、 C、 D、

查看试题解析
5. 下列关于等腰三角形的叙述错误的是（）

A、等腰三角形两底角相等 B、等腰三角形底边上的高线、底边上的中线、顶角的角平分线互相重合 C、等腰三角形的三边相等 D、等腰三角形是轴对称图形但不是中心对称图形

查看试题解析
6. 不等式x+3＞0的解集是（）

A、 $x > 3$ B、 $x > - 3$ C、 $x < 3$ D、 $x < - 3$

查看试题解析
7. 下列选项中能由下图平移得到的是（）

A、 B、 C、 D、

查看试题解析
8. 如图所示， $Δ A B C$ 中， $A B = A C$ ， $D$ 是 $B C$ 上一点， $D E ⊥ A B$ 于点 $E$ ，若 $∠ A = 50 °$ ，则 $∠ B D E$ 的度数是（）

A、 $65 °$ B、 $50 °$ C、 $30 °$ D、 $25 °$

查看试题解析
9. 如图，点A、B、C、D、O都在方格纸的格点上，若△COD是由△AOB绕点O按逆时针方向旋转而得，则旋转的角度为（）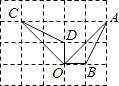

A、30° B、45° C、90° D、135°

查看试题解析
10. 如图，在△ABC中，AD平分∠BAC，DE⊥AB于E， $S_{△ ABC}$ =15，DE=3，AB=6，则AC长是（）

A、4 B、5 C、6 D、7

查看试题解析

二、填空题

11. 不等式组 ${\begin{array}{l} 2 x - 1 \leq 7 \\ 3 x < 6 \end{array}$ 的解集是．

查看试题解析
12. 不等式 $x - 1 \geq 3$ 的最小整数解是．

查看试题解析
13. 等腰三角形的底角是70°，那么它的顶角的度数是．

查看试题解析
14. 如图所示，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $∠ A = 45 °$ ，若 $B C = 2$ ，则 $A B =$ ．

查看试题解析
15. 在平面直角坐标系中，把点 $(1, - 2)$ 向上平移 $3$ 个单位后的坐标是．

查看试题解析
16. 如图，过等边△ABC的顶点A作射线．若∠1＝20°，则∠2的度数为．

查看试题解析
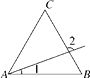17. 如图，在△ABC中，∠C=90°，∠B=30°，AB的垂直平分线ED交AB于点E，交BC于点D，若CD=3，则BD的长为．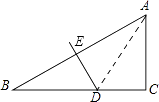

查看试题解析

三、解答题

18. 解不等式： $6 (x - 1) > 3 + 4 x$

查看试题解析
19. 如图所示，在四边形 $A B C D$ 中， $A D / / B C$ ， $B C = 5$ ， $A B = 4$ ， $A E$ 平分 $∠ B A D$ 交 $B C$ 边于点 $E$ ，求 $C E$ 的长．

查看试题解析
20. 如图所示，在边长 $1$ 为的正方形网格中， $Δ A B C$ 的三个顶点和点 $D$ 都在小方格的顶点上，请你平移 $Δ A B C$ ，使点 $A$ 平移到点 $D$ ，得到 $Δ D E F$ ．

查看试题解析
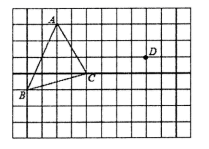21.

(1)、解不等式组，并把解集表示在数轴上： ${\begin{array}{l} 2 x + 3 \geq 5 \\ 3 x - 2 \leq 4 \end{array}$

(2)、求（1）中不等式组的整数解．

查看试题解析
22. 如图所示，已知在 $R t Δ A B C$ 中， $∠ C = 90^{\circ}$ ， $∠ A = 30 °$ ，沿过 $B$ 点的一条直线 $B E$ 折叠这个三角形，使 $C$ 点与 $A B$ 边上的一点 $D$ 重合．

(1)、求证：点 $D$ 为 $A B$ 的中点．

(2)、若 $D E = 1$ ，求 $Δ A B C$ 的面积．

查看试题解析
23. 我市为鼓励居民节约用水，对每户用水按如下标准收费：若每户每月用水不超过 $8 m^{3}$ ，则每立方米按 $1$ 元收费；若每户每月用水超过 $8 m^{3}$ ，则超过部门每立方米按 $2$ 元收费．

(1)、小亮家 $5$ 月份用水 $11 m^{3}$ ，应交纳水费元．

(2)、设小亮家 $6$ 月份用水 $x m^{3}$ ， $(x > 8)$ ，交纳水费 $y$ 元．求 $y$ 关于 $x$ 的函数解析式．

(3)、小亮家要想每月水费不超过 $20$ 元，那么每月的用水量最多不超过多少立方米？

查看试题解析
24. 如图所示，点 $O$ 是平面直角坐标系的原点，点 $A$ 在 $x$ 轴上，等边三角形 $Δ A O C$ 的边长为 $2$

(1)、写出 $Δ A O C$ 的顶点 $C$ 的坐标：．

(2)、将 $Δ A O C$ 沿 $x$ 轴向右平移得到 $Δ O B D$ ，则平移的距离是；将 $Δ A O C$ 绕原点 $O$ 按顺时针方向旋转得到 $Δ O B D$ ，则旋转角至少是度．

(3)、连接 $A D$ ，交 $O C$ 于点 $E$ ，求 $∠ A E O$ 的度数．

查看试题解析
25. 如图所示，已知在 $Δ A B C$ 中， $A B = A C = 10 c m ， B C = 8 c m$ ， $D$ 为 $A B$ 中点．点 $P$ 在线段 $B C$ 上以 $2 c m / s$ 的速度由 $B$ 点向 $C$ 点运动，点 $Q$ 在线段 $C A$ 上以 $\frac{5}{2} c m / s$ 的速度由 $C$ 点向 $A$ 点运动， $P$ 、 $Q$ 两点同时出发．

(1)、设运动时间为 $t$ ，则 $B P$ 的距离可表示为； $C Q$ 的距离可表为．

(2)、在点 $P$ 、 $Q$ 的运动过程中，存在某一时刻，使得 $△ B P D ≅ △ C P Q$ 吗？若存在，求出此时 $t$ 的值；若不存在，请说明理由．

(3)、若点 $P$ 、 $Q$ 均以原来的速度按逆时针方向沿 $△ A B C$ 的三边循环运动，经过多长时间点 $P$ 与点 $Q$ 第一次相遇？此时它们在哪条边上？

查看试题解析