安徽省合肥市庐江三中2019-2020学年八年级下学期数学期中试卷

试卷更新日期：2021-03-23 类型：期中考试

进入出卷网下载

一、单选题

1. 函数 $y = \frac{x - 2}{x - 1} + \sqrt{x + 1}$ 的自变量x的取值范围为 $($ $)$

A、 $x \neq 1$ B、 $x > - 1$ C、 $x \geq - 1$ D、 $x \geq - 1$ 且 $x \neq 1$

查看试题解析
2. 在下列四组数中，不是勾股数的一组数是（　　）

A、a=15，b=8，c=17 B、a=9，b=12，c=15 C、a=7，b=24，c=25 D、a=3，b=5，c=7

查看试题解析
3. 下列二次根式中，与 $\sqrt{6}$ 是同类二次根式的是（）

A、 $\sqrt{12}$ B、 $\sqrt{18}$ C、 $\sqrt{\frac{2}{3}}$ D、 $\sqrt{30}$

查看试题解析
4. 如图，直线L上有三个正方形a，b，c，若a，c的面积分别为1和9，则b的面积为（）

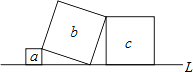A、8 B、9 C、10 D、11

查看试题解析
5. 如图所示，▱ABCD的对角线AC，BD相交于点O，AE=EB，OE=3，AB=5，▱ABCD的周长（）

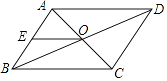A、11 B、13 C、16 D、22

查看试题解析
6. 如图，在▱ABCD中，AB=3，AD=5，∠BCD的平分线交BA的延长线于点E，则AE的长为（）

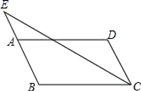A、3 B、2.5 C、2 D、1.5

查看试题解析
7. 若正比例函数 $y = k x$ （ $k \neq 0$ 的常数）的图象在第二、四象限，则一次函数 $y = 2 x + k$ 的图象大致位置是（）

A、 B、 C、 D、

查看试题解析
8. 在△ABC中，AB=10，AC=2 $\sqrt{10}$ ，BC边上的高AD=6，则另一边BC等于（）

A、10 B、8 C、6或10 D、8或10

查看试题解析
9. 如图，点O是矩形ABCD的对角线AC的中点，OM//AB交AD于点M，若OM=3，BC=10，则OB的长为（）

A、5 B、4 C、 $\frac{\sqrt{34}}{2}$ D、 $\sqrt{34}$

查看试题解析
10. 如图，点 $E$ 、 $F$ 、 $G$ 、 $H$ 分别是四边形 $A B C D$ 边 $A B$ 、 $B C$ 、 $C D$ 、 $D A$ 的中点，则下列说法：
①若 $A C = B D$ ，则四边形 $E F G H$ 为矩形；

②若 $A C ⊥ B D$ ，则四边形 $E F G H$ 为菱形；

③若四边形 $E F G H$ 是平行四边形，则 $A C$ 与 $B D$ 互相垂直平分；

④若四边形 $E F G H$ 是正方形，则 $A C$ 与 $B D$ 互相垂直且相等.

其中正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 已知a、b、c是△ABC三边的长，且满足关系式 $\sqrt{c^{2} - a^{2} - b^{2}} + | a - b | = 0$ ，
则△ABC的形状为

查看试题解析
12. 若 $y = \sqrt{x - \frac{1}{3}} + \sqrt{\frac{1}{3} - x} - 9$ ，则 $x y =$ .

查看试题解析
13. 如图，在正方形 $A B C D$ 中，点 $F$ 为 $C D$ 上一点， $B F$ 与 $A C$ 交于点 $E$ ，若 $∠ C B F = 20 °$ ，则 $∠ A E D$ 等于 $°$ ．

查看试题解析
14. 如图，在矩形纸片ABCD中，AB=12，BC=5，点E在AB上，将△DAE沿DE折叠，使点A落在对角线BD上的点A′处，则AE的长为．

查看试题解析

三、解答题

15. 计算：

(1)、 $2 \sqrt{12} - 6 \sqrt{\frac{1}{3}} + 3 \sqrt{48}$

(2)、 $(\sqrt{5} - 2) (2 + \sqrt{5}) - {(- \sqrt{3})}^{2} + \sqrt{8} \times \frac{1}{\sqrt{2}}$

查看试题解析
16. 先化简，在求值： $(\frac{5 x + 3 y}{x^{2} - y^{2}} + \frac{2 x}{y^{2} - x^{2}}) \div \frac{1}{x^{2} y - x y^{2}}$ ，其中， $x = \sqrt{3} + \sqrt{2}$ ， $y = \sqrt{3} - \sqrt{2}$ .

查看试题解析
17. 如图所示，在四边形 $A B C D$ 中， $A B$ ， $B C$ ， $C D$ ， $D A$ 的长分别为2，2， $2 \sqrt{3}$ ，2，且 $A B ⊥ B C$ ，求 $∠ B A D$ 的度数.

查看试题解析
18. 如图，直线l是一次函数y＝kx+b的图象．

(1)、求出这个一次函数的解析式．

(2)、根据函数图象，直接写出y＜2时x的取值范围．

查看试题解析
19. 如图：正方形网格中每个小方格的边长为1，且点A、B、C均为格点．

(1)、求 $△ A B C$ 的面积；

(2)、通过计算判断 $△ A B C$ 的形状；

(3)、求AB边上的高．

查看试题解析
20. 如图，在▱ABCD中，AE⊥BD，CF⊥BD，垂足分别为E、F．求证：

(1)、AE＝CF；

(2)、四边形AECF是平行四边形．

查看试题解析
21. 你一定玩过荡秋千的游戏吧，小明在荡秋千时发现：如图，当秋千 $A B$ 在静止位置时，下端 $B$ 离地面0.5米，当秋千荡到 $A C$ 位置时，下端 $C$ 距静止时的水平距离 $C D$ 为4米，距地面2.5米，请你计算秋千 $A B$ 的长.

查看试题解析
22. 如图，矩形ABCD的对角线AC、BD相交于点O，DE∥AC，CE∥BD．

(1)、求证：四边形OCED为菱形；

(2)、连接AE、BE，AE与BE相等吗？请说明理由．

查看试题解析
23. 如图，正方形ABCD的对角线AC，BD相交于点O，点E是AC的一点，连接EB，过点A做AM⊥BE，垂足为M，AM与BD相交于点F.

(1)、猜想：如图（1）线段OE与线段OF的数量关系为；

(2)、拓展：如图（2），若点E在AC的延长线上，AM⊥BE于点M，AM、DB的延长线相交于点F，其他条件不变，（1）的结论还成立吗？如果成立，请仅就图（2）给出证明；如果不成立，请说明理由.

查看试题解析