天津市红桥区2020年中考数学二模试卷
试卷更新日期:2021-03-23 类型:中考模拟
一、单选题
-
1. 计算 的结果等于A、-8 B、8 C、-2 D、22. 的值等于( )A、 B、 C、1 D、3. 在一些汉字的美术字中,有的是轴对称图形.下面四个美术字中可以看作轴对称图形的是( )A、
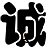 B、
B、 C、
C、 D、
D、 4. 据 年 月 日学习强国APP天津学习平台报道,疫情防控期间,南水北调引江中线工程日均向天津市输水 .将 用科学记数法表示应为( )A、 B、 C、 D、5. 下图是一个由5个相同的正方体组成的立体图形,它的三视图是( )
4. 据 年 月 日学习强国APP天津学习平台报道,疫情防控期间,南水北调引江中线工程日均向天津市输水 .将 用科学记数法表示应为( )A、 B、 C、 D、5. 下图是一个由5个相同的正方体组成的立体图形,它的三视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 估计 的值在( )A、1和2之间 B、2和3之间 C、3和4之间 D、4和5之间7. 分式方程 的解是( )A、 B、 C、 D、8. 二元一次方程组 的解为( )A、 B、 C、 D、9. 已知点 , , 在反比例函数 的图象上,则 , , 的大小关系是( )A、 B、 C、 D、10. 点 在数轴上的位置如图所示,其对应的实数分别是 ,下列结论正确的是( )
6. 估计 的值在( )A、1和2之间 B、2和3之间 C、3和4之间 D、4和5之间7. 分式方程 的解是( )A、 B、 C、 D、8. 二元一次方程组 的解为( )A、 B、 C、 D、9. 已知点 , , 在反比例函数 的图象上,则 , , 的大小关系是( )A、 B、 C、 D、10. 点 在数轴上的位置如图所示,其对应的实数分别是 ,下列结论正确的是( ) A、 B、 C、 D、11. 如图,在 中,将 沿AC折叠后,点D恰好落在DC的延长线上的点E处.若 , ,则 的周长为( )
A、 B、 C、 D、11. 如图,在 中,将 沿AC折叠后,点D恰好落在DC的延长线上的点E处.若 , ,则 的周长为( )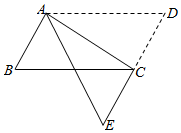 A、12 B、15 C、18 D、2112. 如图,抛物线 与 轴交于点 ,与y轴的交点 在点 与点 之间(不包括这两点),对称轴为直线 .有下列结论:
A、12 B、15 C、18 D、2112. 如图,抛物线 与 轴交于点 ,与y轴的交点 在点 与点 之间(不包括这两点),对称轴为直线 .有下列结论:① ;② ;③ ;④若点 , 在抛物线上,则 .其中正确结论的个数是( )
 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
13. 计算 的结果等于 .14. 计算 的结果等于 .15. 一个不透明的袋子中装有7个球,其中2个红球、5个黑球,这些球除颜色外无其他差别.现从袋子中随机摸出一个球,则它是黑球的概率是 .16. 若一个一次函数的图象经过点 ,则这个一次函数的解析式可以是(写出一个即可) .17. 如图,在 中, , , ,点 , 分别是边 , 的中点, 的平分线与 交于点 ,则 的长为 .

三、解答题
-
18. 如图,在每个小正方形的边长为 的网格中,点 ,点 均落在格点上, 为⊙ 的直径.
 (1)、 的长等于;(2)、请在如图所示的网格中,用无刻度的直尺,画出一个以 为斜边、面积为 的 ,并简要说明点 的位置是如何找到的(不要求证明).19. 解不等式组 ,请结合题意填空,完成本题的解答.(1)、解不等式①,得;(2)、解不等式②,得;(3)、把不等式①和②的解集在数轴上表示出来:
(1)、 的长等于;(2)、请在如图所示的网格中,用无刻度的直尺,画出一个以 为斜边、面积为 的 ,并简要说明点 的位置是如何找到的(不要求证明).19. 解不等式组 ,请结合题意填空,完成本题的解答.(1)、解不等式①,得;(2)、解不等式②,得;(3)、把不等式①和②的解集在数轴上表示出来: (4)、原不等式组的解集为 .20. 为了了解某校九年级学生体育测试成绩情况,现从中随机抽取部分学生的体育成绩,并用得到的数据绘制了统计图①和图②,请根据图中提供的信息,回答下列问题:
(4)、原不等式组的解集为 .20. 为了了解某校九年级学生体育测试成绩情况,现从中随机抽取部分学生的体育成绩,并用得到的数据绘制了统计图①和图②,请根据图中提供的信息,回答下列问题: (1)、本次随机抽样调查的学生人数为 , 图①中的 的值为;(2)、求本次抽样调查获取的样本数据的众数、中位数和平均数;(3)、若该校九年级共有学生300人,如果体育成绩达28以上(含28分)为优秀,请估计该校九年级学生体育成绩达到优秀的人数.21. 已知 是⊙ 的直径,弦 与 相交于点 , .
(1)、本次随机抽样调查的学生人数为 , 图①中的 的值为;(2)、求本次抽样调查获取的样本数据的众数、中位数和平均数;(3)、若该校九年级共有学生300人,如果体育成绩达28以上(含28分)为优秀,请估计该校九年级学生体育成绩达到优秀的人数.21. 已知 是⊙ 的直径,弦 与 相交于点 , . (1)、如图①,若 为 的中点,求 和 的大小;(2)、如图②,过点 作⊙ 的切线,与 的延长线交于点 若 求 的大小.22. 如图,一艘小船以 的速度向正北方向航行,在 处测得灯塔 在北偏东 方向,航行 后到达 处,测得灯塔 在南偏东 方向,求 处距离灯塔 的距离 (结果保留1位小数).参考数据: , , .
(1)、如图①,若 为 的中点,求 和 的大小;(2)、如图②,过点 作⊙ 的切线,与 的延长线交于点 若 求 的大小.22. 如图,一艘小船以 的速度向正北方向航行,在 处测得灯塔 在北偏东 方向,航行 后到达 处,测得灯塔 在南偏东 方向,求 处距离灯塔 的距离 (结果保留1位小数).参考数据: , , . 23. 某公司到果园基地购买某种水果慰问医务工作者,果园基地向购买超过 以上(含 )的客户推出两种购买方式.方式甲:价格为9元 ,由果园基地运送到公司;方式乙:价格为8元 ,由顾客自己租车运回,从果园基地到公司的租车费用为5000元.设该公司购买水果的数量为 ( ).(1)、根据题意,填写下表:
23. 某公司到果园基地购买某种水果慰问医务工作者,果园基地向购买超过 以上(含 )的客户推出两种购买方式.方式甲:价格为9元 ,由果园基地运送到公司;方式乙:价格为8元 ,由顾客自己租车运回,从果园基地到公司的租车费用为5000元.设该公司购买水果的数量为 ( ).(1)、根据题意,填写下表:购买水果的数量(kg)
3500
4500
5500
…
方式甲的总费用(元)
40500
…
方式乙的总费用(元)
41000
…
(2)、设该公司按方式甲购买水果的总费用为 元,按方式乙购买水果的总费用为 元,分别求 , 关于 的函数解析式;(3)、根据题意填空:① 若按方式甲购买水果的总费用和按方式乙购买水果的总费用相同,则该公司购买水果的数量为 ;
② 若该公司购买水果的数量为 ,则按方式甲、方式乙中的方式购买水果的总费用少;
③ 若该公司购买水果的总费用为 元,则按方式甲、方式乙中的方式购买水果的数量多.
24. 在平面直角坐标系中,点 ,点 .将 绕点 顺时针旋转,得 ,点 , 旋转后的对应点为 , .记旋转角为 . (1)、如图①,当 时,求点 的坐标;(2)、如图②,当 时,求点 的坐标;(3)、连接 ,设线段 的中点为 ,连接 ,求线段 的长的最小值(直接写出结果即可).25. 抛物线 ( 为常数, )与 轴交于 , 两点,与 轴交于 点.设该抛物线的顶点为 ,其对称轴与 轴的交点为 .(1)、求该抛物线的解析式;(2)、 为线段 (含端点 )上一点, 为 轴上一点,且 .
(1)、如图①,当 时,求点 的坐标;(2)、如图②,当 时,求点 的坐标;(3)、连接 ,设线段 的中点为 ,连接 ,求线段 的长的最小值(直接写出结果即可).25. 抛物线 ( 为常数, )与 轴交于 , 两点,与 轴交于 点.设该抛物线的顶点为 ,其对称轴与 轴的交点为 .(1)、求该抛物线的解析式;(2)、 为线段 (含端点 )上一点, 为 轴上一点,且 .①求 的取值范围;
②当 取最大值时,将线段 向上平移 个单位长度,使得线段 与抛物线有两个交点,求 的取值范围.