天津市和平区2020年中考数学三模试卷

试卷更新日期：2021-03-23 类型：中考模拟

进入出卷网下载

一、单选题

1. 计算 $(- 5) \div \frac{1}{5}$ 的结果等于（）

A、-25 B、-1 C、1 D、25

查看试题解析
2. tan45°的值等于（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{\sqrt{3}}{2}$ D、1

查看试题解析
3. 民族图案是数学文化中的一块瑰宝．下列图案中，既不是中心对称图形也不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 环境污染刻不容缓，据统计全球每分钟约有8521000吨污水排出，把8521000用科学记数法表示（）

A、 $0.8521 \times 10^{6}$ B、 $0.8521 \times 10^{7}$ C、 $8.521 \times 10^{6}$ D、 $8.521 \times 10^{7}$

查看试题解析
5. 如图是一个由5个相同的正方体组成的立体图形，它的左视图是（）

A、 B、 C、 D、

查看试题解析
6. 估算 $\sqrt{24}$ ＋3的值（）

A、在5和6之间 B、在6和7之间 C、在7和8之间 D、在8和9之间

查看试题解析
7. 计算 $\frac{a}{{(a + b)}^{2}} + \frac{b}{{(a + b)}^{2}}$ 的结果为（）

A、1 B、 $\frac{1}{a} + \frac{1}{b}$ C、a+b D、 $\frac{1}{a + b}$

查看试题解析
8. 在平面直角坐标系中，矩形 $A B C D$ 的位置如图所示，其中 $B (- 1 ， - 1)$ ，点 $A$ 在第二象限， $A B // y$ 轴， $A B = 3 ， B C = 4$ ，则顶点 $D$ 的坐标为（）

A、 $(3 ， 2)$ B、 $(2 ， 2)$ C、 $(3 ， 3)$ D、 $(2 ， 3)$

查看试题解析
9. 方程组 ${\begin{array}{l} x + 2 y = 2 \\ 2 x - y = - 6 \end{array}$ ，的解是（）

A、 ${\begin{array}{l} x = - 2 \\ y = 4 \end{array}$ B、 ${\begin{array}{l} x = - 2 \\ y = 2 \end{array}$ C、 ${\begin{array}{l} x = - 4 \\ y = - 1 \end{array}$ D、 ${\begin{array}{l} x = - 4 \\ y = 1 \end{array}$

查看试题解析
10. 若点 $A (x_{1} ， 1) ， B (x_{2} ， 2) ， C (x_{3} ， - 3)$ 在反比例函数 $y = \frac{6}{x}$ 的图象上，则 $x_{1} ， x_{2} ， x_{3}$ 的大小关系是（）

A、 $x_{3} < x_{1} < x_{2}$ B、 $x_{1} < x_{2} < x_{3}$ C、 $x_{2} < x_{1} < x_{3}$ D、 $x_{3} < x_{2} < x_{1}$

查看试题解析
11. 如图，在边长为2的等边三角形 $A B C$ 中， $D$ 为边 $B C$ 上一点，且 $B D = \frac{1}{2} C D$ ．点 $E$ ， $F$ 分别在边 $A B ， A C$ 上，且 $∠ E D F = 90^{°} ， M$ 为边 $E F$ 的中点，连接 $C M$ 交 $D F$ 于点 $N$ ．若 $D F // A B$ ，则 $C M$ 的长为（）

A、 $\frac{2}{3} \sqrt{3}$ B、 $\frac{3}{4} \sqrt{3}$ C、 $\frac{5}{6} \sqrt{3}$ D、 $\sqrt{3}$

查看试题解析
12. 已知二次函数 $y = - x^{2} + x + 6$ 及一次函数 $y = 2 x - m$ ，将该二次函数在 $x$ 轴上方的图象沿x轴翻折到x轴下方，图象的其余部分不变，得到一个新函数的图象(如图所示)，当直线 $y = 2 x - m$ 与新函数图象有4个交点时，m的取值范围是（）

A、 $- 4 < m < 6$ B、 $- \frac{25}{4} < m < - 4$ C、 $6 < m < \frac{33}{4}$ D、 $- \frac{25}{4} < m < 6$

查看试题解析

二、填空题

13. 计算 ${(- a)}^{2} \cdot {(- a)}^{3}$ 的结果等于．

查看试题解析
14. 计算 $(\sqrt{3} + 2) (\sqrt{3} - 2)$ 的结果等于．

查看试题解析
15. 不透明袋子中装有13个球，其中有2个红球、5个黄球和6个蓝球，这些球除颜色外无其他差别．从袋子中随机取出1个球，则它是蓝球的概率是．

查看试题解析
16. 将直线 $y = 2 x + 1$ 向右平移2个单位，得到的直线解析式为．

查看试题解析
17. 如图，在矩形 $A B C D$ 中， $A B = 3 ， B C = 5$ ，对角线 $A C ， B D$ 交于点 $O$ ．点 $M ， N$ 分别在边 $B C$ 和 $C B$ 的延长线上．将 $△ N O M$ 沿 $N M$ 方向平移，得 $△ B Q P$ ，点 $N ， O ， M$ 的对应点分别为 $B ， Q ， P$ ．再将 $△ B Q P$ 沿 $B Q$ 翻折，点 $P$ 恰好落在点 $D$ 上．此时点 $Q$ 在 $P D$ 上．则 $△ N O M$ 平移的距离为．

查看试题解析

三、解答题

18. 如图，在每个小正方形边长为1的网格中，点 $A ， B ， C ， D$ 均在格点上， $A C ， B D$ 交于点 $P$ ．

(1)、 $\tan ∠ A B D$ 的值为；

(2)、若点 $M$ 在线段 $A B$ 上，当 $P M + \frac{\sqrt{2}}{2} B M$ 取得最小值时，请在如图所示的网格中用无刻度的直尺，画出点 $M$ ，并简要说明点 $M$ 的位置是如何找到的(不要求证明)．

查看试题解析
19. 解不等式组 ${\begin{array}{l} - 3 x + 6 > 4 - x \\ 3 (1 + x) < 6 + 4 x \end{array} \begin{matrix} ① \\ ② \end{matrix}$
请结合题意填空，完成本题的解答．

(1)、解不等式①，得；

(2)、解不等式②，得；

(3)、把不等式①和②的解集在数轴上表示出来；

(4)、原不等式组的解集为．

查看试题解析
20. 我校八年级有800名学生，在体育中考前进行一次排球模拟测试，从中随机抽取部分学生，根据其测试成绩制作了下面两个统计图，请根据相关信息，解答下列问题：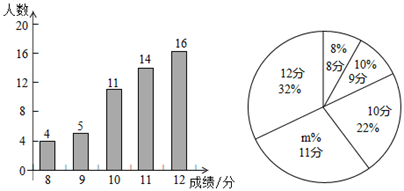

(1)、本次抽取到的学生人数为，图2中 $m$ 的值为.

(2)、本次调查获取的样本数据的平均数是，众数是，中位数是.

(3)、根据样本数据，估计我校八年级模拟体测中得12分的学生约有多少人？

查看试题解析
21. 已知在 $△ A B C$ 中， $B C ⊥ A B$ ． $A B$ 是 $⊙ O$ 的弦， $A C$ 交 $⊙ O$ 于点 $D$ ，且 $D$ 为 $A C$ 的中点，延长 $C B$ 交 $⊙ O$ 于点 $E$ ，连接 $A E$ ．

(1)、如图①，若 $∠ E = 50^{°}$ ，求 $∠ E A C$ 的大小；

(2)、如图②，过点 $E$ 作 $⊙ O$ 的切线，交 $A C$ 的延长线于点 $F$ ．若 $C F = 2 C D$ ，求 $∠ C A B$ 的大小．

查看试题解析
22. 学完三角函数知识后，某校“数学社团”的小明和小华决定用自己学到的知识测量纪念塔的高度．如图， $C D$ 是高为 $1 m$ 的测角仪，在 $D$ 处测得塔顶端 $A$ 的仰角为40°，向塔方向前进 $40 m$ 在 $E$ 处测得塔顶端 $A$ 的仰角为63.4°，求纪念塔 $A B$ 的高度(结果取整数)．
参考数据： $\sin 40^{°} \approx 0.64 ， \cos 40^{°} \approx 0.77 ， \tan 40^{°} \approx 0.84 ， \tan {63.4}^{°} \approx 2.00$ ．

查看试题解析

23. 某校开展“文明在行动”的志愿者活动，准备购买某一品牌书包送到希望学校．在

A

商店，无论一次购买多少，价格均为每个50元．在

B

商店，一次购买数量不超过10个时，价格为每个60元；一次购买数量超过10个时，超出10个部分打八折．设一次购买该品牌书包的数量为x个．

(1)、根据题意填表：

一次购买数量/个	5	10	15	…
$A$ 商店花费/元		500		…
$B$ 商店花费/元		600		…

(2)、设在

A

商店花费

y_{1}

元，在

B

商店花费

y_{2}

元，分别求出

y_{1}, y_{2}

关于

x

的函数解析式；

(3)、根据题意填空；

①若小丽在 $A$ 商店和在 $B$ 商店一次购买书包的数量相同，且花费相同，则她在同一商店一次购买书包的数量为个．

②若小丽在同一商店一次购买书包的数量为50个，则她在 $A, B$ 两个商店中的商店购买花费少；

③若小丽在同一商店一次购买书包花费了1800元，则她在 $A, B$ 两个商店中商店购买数量多．

查看试题解析

24. 在平面直角坐标系中， $O$ 为原点，点 $A (- 3 ， 0)$ ，点 $B (0 ， \sqrt{3})$ ．以 $A B$ 为一边作等边三角形 $A B C$ ，点 $C$ 在第二象限．

(1)、如图①，求点 $C$ 的坐标；

(2)、将 $△ A O B$ 绕点 $B$ 顺时针旋转得 $△ A^{'} O^{'} B$ ，点 $A ， O$ 旋转后的对应点为 $A^{'} ， O^{'}$ ．
①如图②，当旋转角为30°时， $A^{'} B ， A^{'} O^{'}$ 与 $A C$ 分别交于点 $E ， F ， A^{'} O^{'}$ 与 $A B$ 交于点 $G$ ，求 $△ A^{'} O^{'} B$ 与 $△ A B C$ 公共部分面积 $S$ 的值；

②若 $P$ 为线段 $C O^{'}$ 的中点，求 $A P$ 长的取值范围(直接写出结果即可)．

查看试题解析
25. 已知二次函数 $y = - x^{2} + b x + 3$ 的图象与 $x$ 轴交于点 $A ， B$ (点 $A$ 在点 $B$ 的左侧)，与 $y$ 轴交于点 $C$ ，顶点为 $D$ ．

(1)、当 $b = 6$ 时，求二次函数的最大值；

(2)、当 $b = 2$ 时，点 $P (0 ， t) (t < - 1)$ 是 $y$ 轴上的点， $Q (- 5 ， 0)$ ，将点 $Q$ 绕点 $P$ 顺时针旋转90°得到点 $E$ ，点 $E$ 恰好落在该二次函数的图象上，求 $t$ 的值；

(3)、 $M$ 是该二次函数图象上的一点，在(Ⅱ)的条件下，连接 $A D ， A E ， B C$ ， $C M$ ，使 $∠ D A E = ∠ M C B$ ，求点 $M$ 的坐标．

查看试题解析