天津市滨海新区2020年中考数学二模试卷
试卷更新日期:2021-03-23 类型:中考模拟
一、单选题
-
1. 计算 的结果等于( )A、-12 B、12 C、-81 D、812. 的值等于( )A、 B、 C、1 D、3. 下列标志中,可以看作是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 中国的领水面积约为370000km2 , 将数370000用科学记数法表示为( )A、37×104 B、3.7×104 C、0.37×106 D、3.7×1055. 下图是一个由5个相同的正方体组成的立体图形,它的左视图是( )
4. 中国的领水面积约为370000km2 , 将数370000用科学记数法表示为( )A、37×104 B、3.7×104 C、0.37×106 D、3.7×1055. 下图是一个由5个相同的正方体组成的立体图形,它的左视图是( ) A、
A、 B、
B、 C、
C、 D、
D、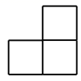 6. 估计 的值在( )A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间7. 计算 的结果为( )A、 B、 C、 D、8. 方程组 的解是( )A、 B、 C、 D、9. 若点 , , 在反比例函数 的图象上,则 的大小关系是( )A、 B、 C、 D、10. 如图,四边形 为菱形,点A的坐标为 ,点C的坐标为 ,点D在y轴上,则点B的坐标为( )
6. 估计 的值在( )A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间7. 计算 的结果为( )A、 B、 C、 D、8. 方程组 的解是( )A、 B、 C、 D、9. 若点 , , 在反比例函数 的图象上,则 的大小关系是( )A、 B、 C、 D、10. 如图,四边形 为菱形,点A的坐标为 ,点C的坐标为 ,点D在y轴上,则点B的坐标为( ) A、 B、 C、 D、11. 如图,将 绕直角顶点C顺时针旋转 ,得 ,连接 ,若 ,则 的大小为( )
A、 B、 C、 D、11. 如图,将 绕直角顶点C顺时针旋转 ,得 ,连接 ,若 ,则 的大小为( ) A、 B、 C、 D、12. 已知抛物线 的对称轴是 ,且 (m为实数)在 范围内有实数根,则m的取值范围是( )A、 B、 C、 D、
A、 B、 C、 D、12. 已知抛物线 的对称轴是 ,且 (m为实数)在 范围内有实数根,则m的取值范围是( )A、 B、 C、 D、二、填空题
-
13. 计算 的结果等于 .14. 计算 的结果等于 .15. 一个不透明的口袋中有8个小球,其中有2个黄球,3个红球和3个绿球,这些球除颜色外无其他差别.从袋子中随机取出1个球,则它是黄球的概率是 .16. 将直线 向下平移3个单位长度,平移后直线的解析式为 .17. 如图,在边长为4的正方形 中,点 分别是 的中点, 与 交于点P,则 的长度为 .
 18. 如图,在每个小正方形的边长为1的网格中, 的顶点 均在格点上.
18. 如图,在每个小正方形的边长为1的网格中, 的顶点 均在格点上.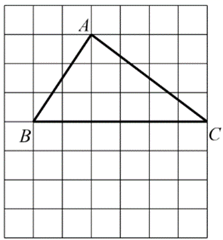 (1)、 的长等于;(2)、请用无刻度的直尺 , 在如图所示的网格中,画出点 ,点E在 上,且 ,点F在 上,使其满足 ,并简要说明点 的位置是如何找到的(不要求证明).
(1)、 的长等于;(2)、请用无刻度的直尺 , 在如图所示的网格中,画出点 ,点E在 上,且 ,点F在 上,使其满足 ,并简要说明点 的位置是如何找到的(不要求证明).三、解答题
-
19. 解不等式组
请结合题意填空,完成本题的解答.
(1)、解不等式①,得;(2)、解不等式②,得;(3)、把不等式①和②的解集在数轴上表示出来: (4)、原不等式组的解集为 .20. 为了解某学校九年级学生每周平均课外阅读时间的情况,随机抽查了该学校九年级部分同学,对其每周平均课外阅读时间进行统计,绘制了如下的统计图①和图②.请根据相关信息,解答下列问题:
(4)、原不等式组的解集为 .20. 为了解某学校九年级学生每周平均课外阅读时间的情况,随机抽查了该学校九年级部分同学,对其每周平均课外阅读时间进行统计,绘制了如下的统计图①和图②.请根据相关信息,解答下列问题: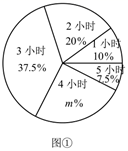
 (1)、该校抽查九年级学生的人数为 , 图①中的m值为;(2)、求统计的这组数据的众数、中位数和平均数.(3)、根据统计的样本数据,估计该校九年级400名学生中,每周平均课外阅读时间大于 的学生人数.21. 如图①,在 中, 为直径,C为 上一点, ,过点C作 的切线,与 的延长线相交于点P.
(1)、该校抽查九年级学生的人数为 , 图①中的m值为;(2)、求统计的这组数据的众数、中位数和平均数.(3)、根据统计的样本数据,估计该校九年级400名学生中,每周平均课外阅读时间大于 的学生人数.21. 如图①,在 中, 为直径,C为 上一点, ,过点C作 的切线,与 的延长线相交于点P.
(Ⅰ)求 的大小;
(Ⅱ)如图②,过点B作 的垂线,垂足为点E,与 的延长线交于点F,
①求 的大小;②若 的半径为2,求 的长.
22. 如图,一艘海轮位于灯塔P的北偏东 方向,距离灯塔 的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东 方向上的B处.这时,B处距离灯塔P有多远(结果取整数)?
(参考数据: , , , 取1.414)
23. 某游泳馆夏季推出两种游泳付费方式.方式一:先购买会员证,每张会员证200元,只限本人当年使用,凭证游泳每次再付费5元;方式二:不购买会员证,每次游泳付费15元.设小强计划今年夏季游泳次数为x(x为正整数).
(1)、根据题意,填写下表:游泳次数
10
15
…
方式一的总费用(元)
250
…
方式二的总费用(元)
150
…
(2)、设小强今年夏季游泳用方式一付费 元,用方式二付费 元,分别写出 关于x的函数关系式;(3)、①若小强今年夏季用方式一和用方式二游泳的次数相同,且费用相同,则小强游泳的次数为次;②若小强用同一种付费方式游泳30次,则他用方式一和用方式二中的方式付费方式,花费少;
③若小强用同一种付费方式游泳花费270元,则用方式一和用方式二中的方式付费方式,游泳的次数多.
24. 如图,将三角形纸片 放在平面直角坐标系中, , , ,点B在x轴的正半轴上,点 是边 上的一个动点(点P不与点O、B重合),过点P作 于点D,沿 折叠该纸片,使点O落在射线 上的Q点处. (1)、用含t的代数式表示线段 的长;(2)、当点Q与点C重合时,求t的值;(3)、设 与四边形 重叠部分的图形的面积为S,求S与t之间的函数关系式;25. 如图,抛物线 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.点A坐标的为 ,点C的坐标为 .
(1)、用含t的代数式表示线段 的长;(2)、当点Q与点C重合时,求t的值;(3)、设 与四边形 重叠部分的图形的面积为S,求S与t之间的函数关系式;25. 如图,抛物线 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.点A坐标的为 ,点C的坐标为 .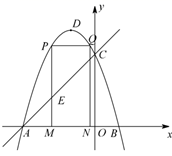 (1)、求抛物线的解析式;(2)、点M为线段 上一点(点M不与点A、B重合),过点M作i轴的垂线,与直线 交于点E,与抛物线交于点P,过点P作 交抛物线于点Q,过点Q作 轴于点N.若点P在点Q左边,当矩形 的周长最大时,求 的面积;(3)、在(2)的条件下,当矩形 的周长最大时,连接 ,过抛物线上一点F作y轴的平行线,与直线 交于点G(点G在点F的上方).若 ,求点F的坐标.
(1)、求抛物线的解析式;(2)、点M为线段 上一点(点M不与点A、B重合),过点M作i轴的垂线,与直线 交于点E,与抛物线交于点P,过点P作 交抛物线于点Q,过点Q作 轴于点N.若点P在点Q左边,当矩形 的周长最大时,求 的面积;(3)、在(2)的条件下,当矩形 的周长最大时,连接 ,过抛物线上一点F作y轴的平行线,与直线 交于点G(点G在点F的上方).若 ,求点F的坐标.