河北省唐山市玉田县2020年中考数学二模试卷
试卷更新日期:2021-03-23 类型:中考模拟
一、单选题
-
1. 在-2,-1,0,1这四个数中,最小的数是( )A、0 B、-1 C、-2 D、12. 在“新冠”疫情期间,成都数字学校开设了语文、数学、英语等36个科目的网络直播课,四川省有1500万人次观看了课程.将数据“1500万”用科学记数法可表示为( )A、1.5×106 B、1.5×107 C、15×106 D、0.15×1083. 如图,直线a∥b,∠1=50°,∠2=40°,则∠3的度数为( )
 A、40° B、90° C、50° D、100°4. 如图一个五边形木架,要保证它不变形,至少要再钉上几根木条( )
A、40° B、90° C、50° D、100°4. 如图一个五边形木架,要保证它不变形,至少要再钉上几根木条( ) A、4 B、3 C、2 D、15. 估计 的值在( )A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间6. 某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与“抗”字所在面相对的面上的汉字是( )
A、4 B、3 C、2 D、15. 估计 的值在( )A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间6. 某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与“抗”字所在面相对的面上的汉字是( )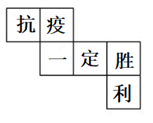 A、一 B、定 C、胜 D、利7. 下列“数字图形”中,既是轴对称图形,又是中心对称图形的有( )
A、一 B、定 C、胜 D、利7. 下列“数字图形”中,既是轴对称图形,又是中心对称图形的有( ) A、1个 B、2个 C、3个 D、4个8. 如图是一个 的方阵,其中每行、每列的两数和相等,则 可以是( )
A、1个 B、2个 C、3个 D、4个8. 如图是一个 的方阵,其中每行、每列的两数和相等,则 可以是( ) A、 B、-1 C、0 D、9. 下列说法正确的是( )A、了解我市市民知晓“礼让行人”交通新规的情况,适合全面调查 B、甲、乙两人跳远成绩的方差分别为S甲2=3,S乙2=4,说明乙的跳远成绩比甲稳定 C、一组数据2,2,3,4的众数是2,中位数是2.5 D、可能性是1%的事件在一次试验中一定不会发生10. 关于x的一元二次方程x2﹣(k+3)x+2k+2=0的根的情况,下面判断正确的是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、有两个实数根 D、无实数根11. 如图,矩形 中, .以点 为圆心,以任意长为半径作弧分别交 、 于点 、 ,再分别以点 、 为圆心,以大于 的长为半径作弧交于点 ,作射线 交 于点 ,若 ,则矩形 的面积等于( )
A、 B、-1 C、0 D、9. 下列说法正确的是( )A、了解我市市民知晓“礼让行人”交通新规的情况,适合全面调查 B、甲、乙两人跳远成绩的方差分别为S甲2=3,S乙2=4,说明乙的跳远成绩比甲稳定 C、一组数据2,2,3,4的众数是2,中位数是2.5 D、可能性是1%的事件在一次试验中一定不会发生10. 关于x的一元二次方程x2﹣(k+3)x+2k+2=0的根的情况,下面判断正确的是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、有两个实数根 D、无实数根11. 如图,矩形 中, .以点 为圆心,以任意长为半径作弧分别交 、 于点 、 ,再分别以点 、 为圆心,以大于 的长为半径作弧交于点 ,作射线 交 于点 ,若 ,则矩形 的面积等于( )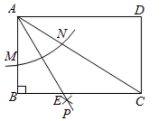 A、 B、 C、 D、12. 如图,在直角坐标系中,已知菱形 的顶点 , .作菱形 关于 轴的对称图形 ,再作图形 关于点 的中心对称图形 ,则点 的对应点 的坐标是( )
A、 B、 C、 D、12. 如图,在直角坐标系中,已知菱形 的顶点 , .作菱形 关于 轴的对称图形 ,再作图形 关于点 的中心对称图形 ,则点 的对应点 的坐标是( )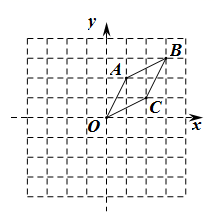 A、 B、 C、 D、13. 在平面直角坐标系中,抛物线 经过变换后得到抛物线 ,则这个变换可以是( )A、向左平移2个单位 B、向右平移2个单位 C、向左平移8个单位 D、向右平移8个单位14. 在如图所示的象棋盘(各个小正方形的边长均相等)中,根据“马走日”的规则,“马”应落在下列哪个位置处,能使“马”、“车”、“炮”所在位置的格点构成的三角形与“帅”、“相”,“兵”所在位置的格点构成的三角形相似( )
A、 B、 C、 D、13. 在平面直角坐标系中,抛物线 经过变换后得到抛物线 ,则这个变换可以是( )A、向左平移2个单位 B、向右平移2个单位 C、向左平移8个单位 D、向右平移8个单位14. 在如图所示的象棋盘(各个小正方形的边长均相等)中,根据“马走日”的规则,“马”应落在下列哪个位置处,能使“马”、“车”、“炮”所在位置的格点构成的三角形与“帅”、“相”,“兵”所在位置的格点构成的三角形相似( ) A、①处 B、②处 C、③处 D、④处15. 如图,正方形 的边长为4,点 是 的中点,点 从点 出发,沿 移动至终点 ,设 点经过的路径长为x, 的面积为y,则下列图象能大致反映y与x函数关系的是( )
A、①处 B、②处 C、③处 D、④处15. 如图,正方形 的边长为4,点 是 的中点,点 从点 出发,沿 移动至终点 ,设 点经过的路径长为x, 的面积为y,则下列图象能大致反映y与x函数关系的是( ) A、
A、 B、
B、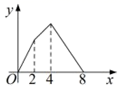 C、
C、 D、
D、 16. 如图,数轴上 、 两点的距离为4,一动点 从点 出发,按以下规律跳动:第1次跳动到 的中点 处,第2次从 点跳动到 的中点 处,第3次从 点跳动到 的中点 处,按照这样的规律继续跳动到点 ( , 是整数)处,问经过这样2020次跳动后的点与 点的距离是( )
16. 如图,数轴上 、 两点的距离为4,一动点 从点 出发,按以下规律跳动:第1次跳动到 的中点 处,第2次从 点跳动到 的中点 处,第3次从 点跳动到 的中点 处,按照这样的规律继续跳动到点 ( , 是整数)处,问经过这样2020次跳动后的点与 点的距离是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
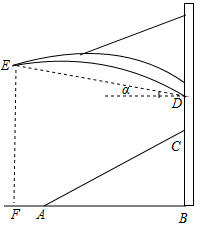
17. 若n﹣2与n+4互为相反数,则n的值为 .18. 某体育看台侧面的示意图如图所示,观众区 的坡度 为 ,顶端 离水平地面 的高度为 ,从顶棚的 处看 处的仰角 ,竖直的立杆上 、 两点间的距离为 , 处到观众区底端 处的水平距离 为 .则观众区的水平宽度 ;顶棚的 处离地面的高度 .( , ,结果精确到 )
 19. 有三个大小一样的正六边形,可按下列方式进行拼接:
19. 有三个大小一样的正六边形,可按下列方式进行拼接:方式1:如图1;
方式2:如图2;
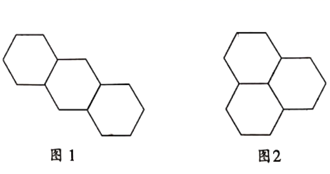
若有四个边长均为1的正六边形,采用方式1拼接,所得图案的外轮廓的周长是.有 个边长均为1的正六边形,采用上述两种方式的一种或两种方式混合拼接,若得图案的外轮廓的周长为18,则n的最大值为 .
三、解答题
-
20. 先化简,再求值: 其中 的值从不等式组 的整数解中选取.21. 为了庆祝中华人民共和国成立70周年,某市决定开展“我和祖国共成长”主题演讲比赛,某中学将参加本校选拔赛的40名选手的成绩(满分为100分,得分为正整数且无满分,最低为75分)分成五组,并绘制了下列不完整的统计图表.
分数段
频数
频率
74.5~79.5
2
0.05
79.5~84.5
m
0.2
84.5~89.5
12
0.3
89.5~94.5
14
n
94.5~99.5
4
0.1
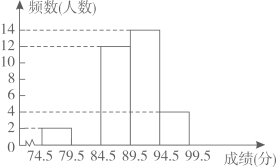 (1)、表中m= , n=;(2)、请在图中补全频数直方图;(3)、甲同学的比赛成绩是40位参赛选手成绩的中位数,据此推测他的成绩落在分数段内;(4)、选拔赛中,成绩在94.5分以上的选手,男生和女生各占一半,学校从中随机确定2名选手参加全市决赛,请用列举法或树状图法求恰好是一名男生和一名女生的概率.22. 如图,认真观察下面这些算式,并结合你发现的规律,完成下列问题:
(1)、表中m= , n=;(2)、请在图中补全频数直方图;(3)、甲同学的比赛成绩是40位参赛选手成绩的中位数,据此推测他的成绩落在分数段内;(4)、选拔赛中,成绩在94.5分以上的选手,男生和女生各占一半,学校从中随机确定2名选手参加全市决赛,请用列举法或树状图法求恰好是一名男生和一名女生的概率.22. 如图,认真观察下面这些算式,并结合你发现的规律,完成下列问题:①32﹣12=(3+1)(3﹣1)=8=8×1,
②52﹣32=(5+3)(5﹣3)=16=8×2,
③72﹣52=(7+5)(7﹣5)=24=8×3,
④92﹣72=(9+7)(9﹣7)=32=8×4.
…
(1)、请写出:算式⑤;
算式⑥;
(2)、上述算式的规律可以用文字概括为:“两个连续奇数的平方差能被8整除”,如果设两个连续奇数分别为2n﹣1和2n+1(n为整数),请说明这个规律是成立的;(3)、你认为“两个连续偶数的平方差能被8整除”这个说法是否也成立呢?请说明理由.23. 如图,在正方形 中, ,点 是 边上一点,连接 ,将线段 绕点 顺时针旋转 得到线段 ,连接 交 于点 ,连接 ,过点 作 交 延长线于点 . (1)、求证: ;(2)、若 ,求线段 绕点 顺时针旋转 所形成的图形面积.24. 小明在妈妈的帮助下,利用社区提供的免费摊点卖玩具,已知小明所有玩具的进价均2元/个.在销售过程中发现:每天玩具销售量 (件)与销售价格 (元/件)的关系如图所示,其中 段为反比例函数图象的一部分, 段为一次函数图象的一部分,设小明销售这种玩具的日利润为 元.
(1)、求证: ;(2)、若 ,求线段 绕点 顺时针旋转 所形成的图形面积.24. 小明在妈妈的帮助下,利用社区提供的免费摊点卖玩具,已知小明所有玩具的进价均2元/个.在销售过程中发现:每天玩具销售量 (件)与销售价格 (元/件)的关系如图所示,其中 段为反比例函数图象的一部分, 段为一次函数图象的一部分,设小明销售这种玩具的日利润为 元. (1)、根据图象,求出 与 之间的函数关系式;(2)、求销售这种玩具的日利润 (元)与 (元/件)之间的函数关系式,并求每天利润的最大值.25. 将 的顶点 放在半圆 上,现从 与半圆 相切于点 (如图1)的位置开始,将 绕着点 顺时针旋转,设旋转角为 ,旋转后 、 分别与半圆 交于点 、 ,连接 (如图2).已知 , , ,半圆 的直径为8.
(1)、根据图象,求出 与 之间的函数关系式;(2)、求销售这种玩具的日利润 (元)与 (元/件)之间的函数关系式,并求每天利润的最大值.25. 将 的顶点 放在半圆 上,现从 与半圆 相切于点 (如图1)的位置开始,将 绕着点 顺时针旋转,设旋转角为 ,旋转后 、 分别与半圆 交于点 、 ,连接 (如图2).已知 , , ,半圆 的直径为8.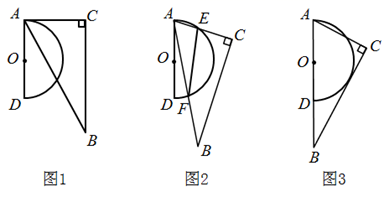 (1)、求图2中 的长;(2)、 绕着点 顺时针旋转到如图3位置时, ,此时边 与⊙O的位置关系是什么?并说明理由;(3)、请直接写出在旋转的过程中,点 到 的距离 的取值范围.26. 如图1,二次函数 的图象过原点,与 轴的另一个交点为 .
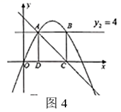
(1)、求图2中 的长;(2)、 绕着点 顺时针旋转到如图3位置时, ,此时边 与⊙O的位置关系是什么?并说明理由;(3)、请直接写出在旋转的过程中,点 到 的距离 的取值范围.26. 如图1,二次函数 的图象过原点,与 轴的另一个交点为 .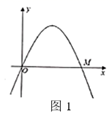 (1)、求该二次函数的解析式;(2)、如图2, 与二次函数 的图象交于点 ,求 的面积;
(1)、求该二次函数的解析式;(2)、如图2, 与二次函数 的图象交于点 ,求 的面积;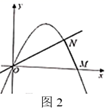 (3)、如图3,直线 与二次函数 的图象交于 、 两点(点 在点 的左侧),过 、 两点分别作 轴的垂线,垂足分别为点 、点 .判断四边形 的形状,并说明理由;
(3)、如图3,直线 与二次函数 的图象交于 、 两点(点 在点 的左侧),过 、 两点分别作 轴的垂线,垂足分别为点 、点 .判断四边形 的形状,并说明理由; (4)、如图4,在(3)的条件下,动点 从点 出发沿射线 以每秒1个单位长度匀速运动,同时动点 以相同的速度从点 出发沿线段 匀速运动,到达点 时立即原速返回,当动点 返回到点 时, 、 两点同时停止运动,设运动时间为 秒( ).过点 向 轴作垂线,交抛物线于点 ,交直线 于点 ,问:以 、 、 、 四点为顶点构成的四边形能否是平行四边形?若能,请直接写出 的值;若不能,请说明理由.
(4)、如图4,在(3)的条件下,动点 从点 出发沿射线 以每秒1个单位长度匀速运动,同时动点 以相同的速度从点 出发沿线段 匀速运动,到达点 时立即原速返回,当动点 返回到点 时, 、 两点同时停止运动,设运动时间为 秒( ).过点 向 轴作垂线,交抛物线于点 ,交直线 于点 ,问:以 、 、 、 四点为顶点构成的四边形能否是平行四边形?若能,请直接写出 的值;若不能,请说明理由.