河北省顺平县2020年中考数学一模试卷
试卷更新日期:2021-03-23 类型:中考模拟
一、单选题
-
1. 下列各数中,比-2大2的数是( )A、0 B、-4 C、2 D、42. 把一个三角板按图所示位置放置,∠1=40°,∠2=( )
 A、40° B、45° C、50° D、60°3. 图中几何体的主视图是( )
A、40° B、45° C、50° D、60°3. 图中几何体的主视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 4. 下列对代数式 的描述,正确的是( )A、a与b的相反数的差 B、a与b的差的倒数 C、a与b的倒数的差 D、a的相反数与b的差的倒数5. 如图,直线a b c,AB= BC,若DF=9,则EF的长度为( )
4. 下列对代数式 的描述,正确的是( )A、a与b的相反数的差 B、a与b的差的倒数 C、a与b的倒数的差 D、a的相反数与b的差的倒数5. 如图,直线a b c,AB= BC,若DF=9,则EF的长度为( ) A、9 B、5 C、4 D、36. 下列变形正确的是( )A、 B、 C、 D、7. 关于x的一元二次方程 有两个不相等的实数根,则a的取值范围是( )A、 B、 C、 D、 且8. 在新型冠状病毒防控期间,小静坚持每天测量自己的体温,并把5次的体温(单位: )分别写在5张完全相同的卡片上:36,36.1,35.9,35.5,背面,把这5张卡片背面朝上洗匀后,从中随机抽取一张卡片,已知P(一次抽到36) ,这5张卡片上数据的方差为( )A、35.9 B、0.22 C、0.044 D、09. 如图, 五边形ABCDE中,AE BC,AC,BE交于点O, 四边形OCDE是平行四边形,若 的面积是5,四边形OCDE的面积是6,则 的面积是( )
A、9 B、5 C、4 D、36. 下列变形正确的是( )A、 B、 C、 D、7. 关于x的一元二次方程 有两个不相等的实数根,则a的取值范围是( )A、 B、 C、 D、 且8. 在新型冠状病毒防控期间,小静坚持每天测量自己的体温,并把5次的体温(单位: )分别写在5张完全相同的卡片上:36,36.1,35.9,35.5,背面,把这5张卡片背面朝上洗匀后,从中随机抽取一张卡片,已知P(一次抽到36) ,这5张卡片上数据的方差为( )A、35.9 B、0.22 C、0.044 D、09. 如图, 五边形ABCDE中,AE BC,AC,BE交于点O, 四边形OCDE是平行四边形,若 的面积是5,四边形OCDE的面积是6,则 的面积是( ) A、2 B、2.5 C、3 D、410. 如图,点 , ,以原点O为位似中心,把线段AB缩短为原来的一半,得到线段CD,其中点C与点A对应,点D与点B对应,则点D的横坐标为( )
A、2 B、2.5 C、3 D、410. 如图,点 , ,以原点O为位似中心,把线段AB缩短为原来的一半,得到线段CD,其中点C与点A对应,点D与点B对应,则点D的横坐标为( )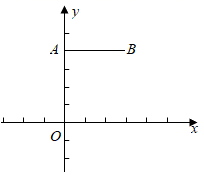 A、2 B、2或-2 C、 D、 或-11. 如图, 在 中, , 在BC上取一点P, 使得 .根据圆规作图的痕迹,可以用直尺成功找到点P的是( )
A、2 B、2或-2 C、 D、 或-11. 如图, 在 中, , 在BC上取一点P, 使得 .根据圆规作图的痕迹,可以用直尺成功找到点P的是( ) A、
A、 B、
B、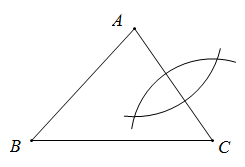 C、
C、 D、
D、 12. 如图,四边形ABCD中,AD//BC, ,CD=BC,点E,F分别是BD,CD的中点,连接AE,EF,AF,若BC=2, ,则BD=( )
12. 如图,四边形ABCD中,AD//BC, ,CD=BC,点E,F分别是BD,CD的中点,连接AE,EF,AF,若BC=2, ,则BD=( ) A、 B、 C、 D、213. 关于x的方程 的解是正数,m的值可能是( )A、 B、 C、0 D、-114. 如图, 在 的正方形网格中, 经过格点A,B,C, 点P是 上任意一点, 连接AP, BP, 则 的值为( )
A、 B、 C、 D、213. 关于x的方程 的解是正数,m的值可能是( )A、 B、 C、0 D、-114. 如图, 在 的正方形网格中, 经过格点A,B,C, 点P是 上任意一点, 连接AP, BP, 则 的值为( ) A、 B、 C、 D、15. 点 是反比例函数 的图象上一点,若 ,则b的值不可能是( )A、-2 B、 C、2 D、316. 如图, 在等边△ABC中, AB=2 , 点D在△ABC内或其边上,AD=2, 以AD为边向右作等边△ADE,连接CD,CE.设CE的最小值为m; 当ED的延长线经过点B时, , 则m, n的值分别为( )
A、 B、 C、 D、15. 点 是反比例函数 的图象上一点,若 ,则b的值不可能是( )A、-2 B、 C、2 D、316. 如图, 在等边△ABC中, AB=2 , 点D在△ABC内或其边上,AD=2, 以AD为边向右作等边△ADE,连接CD,CE.设CE的最小值为m; 当ED的延长线经过点B时, , 则m, n的值分别为( ) A、 ,55 B、 ,60 C、2 -2,55 D、2 -2,60
A、 ,55 B、 ,60 C、2 -2,55 D、2 -2,60二、填空题
-
17. 若单项式 与 是同类项, 则n的值为 .18. 定义新运算:对于任意实数a,b,都有 ,等式右边是通常的加法、减法及乘法运算,比如: .(1)、 .(2)、若 的值等于-5,则x= .19. 如图, 中,AB=7,BC=5,CH⊥AB于点H,CH=4, 点P从点D出发, 以每秒1个单位长度的速度沿DC-CH向点H运动,到点H停止,设点P的运动时间为t
 (1)、AH= .(2)、若△PBC是等腰三角形, 则t的值为 .
(1)、AH= .(2)、若△PBC是等腰三角形, 则t的值为 .三、解答题
-
20. 如图,在一条不完整的数轴上,从左到右的点A,B,C把数轴分成①②③④四部分,点A,B,C对应的数分别是a,b,c,已知bc<0.
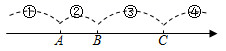 (1)、请说明原点在第几部分;(2)、若AC=5,BC=3,b=-1,求a(3)、若点B到表示1的点的距离与点C到表示1的点的距离相等,且 ,求 的值.21. 发现:小明经过计算总结出两位数乘11的速算方法:头尾一拉,中间相加,满十进一
(1)、请说明原点在第几部分;(2)、若AC=5,BC=3,b=-1,求a(3)、若点B到表示1的点的距离与点C到表示1的点的距离相等,且 ,求 的值.21. 发现:小明经过计算总结出两位数乘11的速算方法:头尾一拉,中间相加,满十进一例1.计算: .
方法:32头尾拉开,中间相加,即3+2=5,满十进一,计算结果为352.
例2.计算:
方法:57头尾拉开,中间相加,即5+7=12,满十进一,计算结果为627
(1)、尝试:.
(2)、 .(3)、 .(4)、探究:一个两位数,十位上的数字是m,个位上的数字是n,这个两位数乘11.若 ,计算结果的百位、十位、个位上的数字分别是什么?请通过计算加以证明
(5)、若 ,直接写出计算结果中十位上的数字.22. 自2020年初的新型状病毒疫情煤发以来.疫情时时刻刻都在牵动全国人民的心.小明在做好自我防控的同时,也从数据分析的角度去看待疫情动态,他从2月10日起.连续7天记录了全国每天新增确诊病例人数.并绘制了如图所示的折线统计图,(注:本题所考查的人数均保留整数) (1)、①小明关注这7天每天新增确诊病例人数的最高值、最低值和中位数,并计算了平均数,其中中位数是 ▲ 人,平均人数是 ▲ 人;
(1)、①小明关注这7天每天新增确诊病例人数的最高值、最低值和中位数,并计算了平均数,其中中位数是 ▲ 人,平均人数是 ▲ 人;②上述哪个统计量能反映这7天新增确诊病例人数的一般水平?
(2)、小明又接着记录了连续5天的全国新增确诊病例人数,如下表:日期/日
17
18
19
20
21
新增确诊病例人数/人
1886
1749
820
889
397
①请在图12中补画出这5天每天新增确诊病例人数的折线统计图;
②求2月10日至2月21日每天新增确诊病例人数的中位数.
(3)、请你分别通过对上述两个中位数的比较和全部折线图来说明每天新增确诊病例人数的升降趋势23. 如图.Rt△ABC中,∠C=90º,AC=BC=4.P是BC上一点(不与B,C重合),连接AP.将AP绕点A逆时针旋转90º得到AQ.连接BQ.分别交AC,AP于点D,E.作QF⊥AC于点F. (1)、求证:QF=AC;(2)、若P是BC的中点, 求tan∠ADQ的值;(3)、若△AEQ的内心在QF上,直接写出BP的长24. 学校计划拿出一笔钱给一些班级配置篮球和排球.若给每班1个篮球和2个排球,花完这笔钱刚好配置30个班:若给每班2个篮球和1个排球,花完这笔钱刚好配置20个班.设每个篮球a元,每个排球b元.(1)、用含b的代数式表示a;(2)、现在给每班x个篮球和y个排球,花完这笔钱刚好配置10个班.
(1)、求证:QF=AC;(2)、若P是BC的中点, 求tan∠ADQ的值;(3)、若△AEQ的内心在QF上,直接写出BP的长24. 学校计划拿出一笔钱给一些班级配置篮球和排球.若给每班1个篮球和2个排球,花完这笔钱刚好配置30个班:若给每班2个篮球和1个排球,花完这笔钱刚好配置20个班.设每个篮球a元,每个排球b元.(1)、用含b的代数式表示a;(2)、现在给每班x个篮球和y个排球,花完这笔钱刚好配置10个班.①求y与x的函数解析式;
②怎样的配置方案,可以使每班配置的排球最少?