河北省石家庄市新华区2020年中考数学四模试卷
试卷更新日期:2021-03-23 类型:中考模拟
一、单选题
-
1. -2020的倒数是( )A、 B、 C、2020 D、-20202. 在下列气温的变化中,能够反映温度上升 的是( )A、气温由 到 B、气温由 到 C、气温由 到 D、气温由 到3. 按图1~图4的步骤作图,下列结论错误的是( )
 A、 B、 C、 D、4. 实数 、 在数轴上的位置如图所示,则a+b的值是( )
A、 B、 C、 D、4. 实数 、 在数轴上的位置如图所示,则a+b的值是( ) A、正数 B、负数 C、0 D、不能确定5. 如图是正方体的表面展开图,则在原正方体中,与“中”字相对的面上的字是( )
A、正数 B、负数 C、0 D、不能确定5. 如图是正方体的表面展开图,则在原正方体中,与“中”字相对的面上的字是( ) A、国 B、必 C、胜 D、疫6. 将一元二次方程 配方后,原方程变形为( )A、 B、 C、 D、7. 用半圆围成一个几何体的侧面,则这个几何体的左视图是( )A、钝角三角形 B、等腰直角三角形 C、等边三角形 D、圆8. 截至2020年2月底,石家庄累计确诊的新型冠状病毒人数为29人,约占石家庄总人数的 ,若 用科学记数法表示成 ,则 的值是( )A、5 B、6 C、-5 D、-69. 如图, 为⊙ 的直径, 为半圆的中点,动点 从点 出发在圆周上顺时针匀速运动,到达点 后停止运动,在点 运动过程中(不包括 、 两点), 的值( )
A、国 B、必 C、胜 D、疫6. 将一元二次方程 配方后,原方程变形为( )A、 B、 C、 D、7. 用半圆围成一个几何体的侧面,则这个几何体的左视图是( )A、钝角三角形 B、等腰直角三角形 C、等边三角形 D、圆8. 截至2020年2月底,石家庄累计确诊的新型冠状病毒人数为29人,约占石家庄总人数的 ,若 用科学记数法表示成 ,则 的值是( )A、5 B、6 C、-5 D、-69. 如图, 为⊙ 的直径, 为半圆的中点,动点 从点 出发在圆周上顺时针匀速运动,到达点 后停止运动,在点 运动过程中(不包括 、 两点), 的值( ) A、由小逐渐增大 B、固定不变为 C、由大逐渐减小 D、固定不变为10. 将一枚质地均匀的骰子连续投掷两次,记投掷两次的正面数字之和为 ,则下面关于事件 发生的概率 说法错误的是( )A、 B、 C、 D、11. 连接正八边形的三个顶点,得到如图所示的图形,下列说法错误的是( )
A、由小逐渐增大 B、固定不变为 C、由大逐渐减小 D、固定不变为10. 将一枚质地均匀的骰子连续投掷两次,记投掷两次的正面数字之和为 ,则下面关于事件 发生的概率 说法错误的是( )A、 B、 C、 D、11. 连接正八边形的三个顶点,得到如图所示的图形,下列说法错误的是( ) A、四边形 与四边形 的面积相等 B、连接 ,则 分别平分 和 C、整个图形是轴对称图形,但不是中心对称图形 D、 是等边三角形12. 若关于x的方程 的解为正数,则m的取值范围是( )A、m<6 B、m>6 C、m<6且m≠0 D、m>6且m≠813. 如图,已知线段 ,按下列步骤作图:分别以 、 为圆心,大于 长为半径画弧,两弧相交于点 、 ,作直线 ,交 于点 ,分别连接 、 、 、 ,如果四边形 是正方形,需要添加的条件是( )
A、四边形 与四边形 的面积相等 B、连接 ,则 分别平分 和 C、整个图形是轴对称图形,但不是中心对称图形 D、 是等边三角形12. 若关于x的方程 的解为正数,则m的取值范围是( )A、m<6 B、m>6 C、m<6且m≠0 D、m>6且m≠813. 如图,已知线段 ,按下列步骤作图:分别以 、 为圆心,大于 长为半径画弧,两弧相交于点 、 ,作直线 ,交 于点 ,分别连接 、 、 、 ,如果四边形 是正方形,需要添加的条件是( ) A、 B、 C、 D、 平分14. 如图,平面直角坐标系中,过点 作 轴于点 ,连接 ,将 绕点 逆时针旋转 , 、 两点的对应点分别为 、 .当双曲线 与 有公共点时, 的取值范围是( )
A、 B、 C、 D、 平分14. 如图,平面直角坐标系中,过点 作 轴于点 ,连接 ,将 绕点 逆时针旋转 , 、 两点的对应点分别为 、 .当双曲线 与 有公共点时, 的取值范围是( )
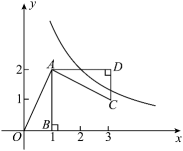 A、 B、 C、 D、15. 如图,在 中,点 在 上, , 是 的角平分线,且 ,当 时, 的长为( )
A、 B、 C、 D、15. 如图,在 中,点 在 上, , 是 的角平分线,且 ,当 时, 的长为( ) A、3 B、4 C、5 D、616. 如图,在 的正方形网格中,动点 、 同时从 、 两点匀速出发,以每秒1个单位长度的速度沿网格线运动至格点 停止.动点 的运动路线为: ;动点 的运动路线为: ,连接 、 .设动点 运动时间为 , 的面积为 ,则 与 之间的函数关系用图象表示大致是( )
A、3 B、4 C、5 D、616. 如图,在 的正方形网格中,动点 、 同时从 、 两点匀速出发,以每秒1个单位长度的速度沿网格线运动至格点 停止.动点 的运动路线为: ;动点 的运动路线为: ,连接 、 .设动点 运动时间为 , 的面积为 ,则 与 之间的函数关系用图象表示大致是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
17. .18. 定义运算 ,当 时,有 ,当 时,有 ,则有:
① ;
②如果 ,那么 的取值范围是 .
19. 曲线 在直角坐标系中的位置如图所示,曲线 是由半径为2,圆心角为 的 ( 是坐标原点,点 在 轴上)绕点 旋转 ,得到 ;再将 绕点 旋转 ,得到 ;……依次类推,形成曲线 ,现有一点 从 点出发,以每秒 个单位长度的速度,沿曲线 向右运动,则点 的坐标为;在第 时,点 的坐标为 .
三、解答题
-
20. 对于题目:“已知 ,求代数式 的值”,采用“整体代入”的方法(换元法),可以比较容易的求出结果.(1)、设 ,则 (用含 的代数式表示);(2)、根据 ,得到 ,所以 的值为;(3)、用“整体代入”的方法(换元法),解决下面问题:
已知 ,求代数式 的值.
21. 观察下列等式,探究发现规律,并解决问题,① ;
② ;
③ ;
(1)、直接写出第④个等式:;(2)、猜想第 个等式(用含字母 的式子表示),并说明这个等式的符合题意性;(3)、利用发现的规律,求 的值.(参考数据: )22. 为了强化学生的环保意识,某校团委在全校举办了“保护环境,人人有责”知识竞赛活动,初、高中根据初赛成绩,各选出5名选手组成初中代表队和高中代表队进行复赛,两个队学生的复赛成绩(满分10分)如图所示: (1)、根据图示填写下表:
(1)、根据图示填写下表:平均分
中位数
众数
方差
初中队
8.5
0.7
高中队
8.5
10
(2)、小明同学说:“这次复赛我得了8分,在我们队中排名属中游偏下!”小明是初中队还是高中队的学生?为什么?(3)、结合两队成绩的平均分、中位数和方差,分析哪个对的复赛成绩较好.23. 如图,在等腰 中, , ,将 绕点 逆时针旋转 ,得到 ,连结 . (1)、求证: ;(2)、四边形 是什么形状的四边形?并说明理由;(3)、直接写出:当 分别是多少度时,① ;② .24. 已知甲、乙两辆汽车分别从 、 两地同时匀速出发,甲车开往 地,乙车开往 地,设甲、乙两车距 地的路程分别为 、 (单位: ),甲车的行驶时间为 (单位: ).若甲车的速度为 , 与 之间的对应关系如下表:
(1)、求证: ;(2)、四边形 是什么形状的四边形?并说明理由;(3)、直接写出:当 分别是多少度时,① ;② .24. 已知甲、乙两辆汽车分别从 、 两地同时匀速出发,甲车开往 地,乙车开往 地,设甲、乙两车距 地的路程分别为 、 (单位: ),甲车的行驶时间为 (单位: ).若甲车的速度为 , 与 之间的对应关系如下表:2
5
560
320
(1)、分别求出 、 与 之间的函数关系式;(不写 的取值范围)(2)、当 为何值时,甲、乙两辆汽车相遇?(3)、当两车距离小于 时,求 的取值范围.25. 如图,在Rt△ABC中,∠ACB=90°,AB=10,BC=6,点O在射线 上(点 不与点 重合),过点 作 ,垂足为 ,以点 为圆心, 为半径画半圆 ,分别交射线 于 、 两点,设 .(1)、如图,当点 为 边的中点时,求 的值;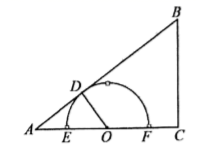 (2)、如图,当点 与点 重合时,连接 ,求弦 的长;
(2)、如图,当点 与点 重合时,连接 ,求弦 的长;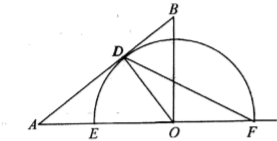 (3)、当半圆 与 无交点时,直接写出 的取值范围.26. 如图,抛物线 经过 , 两点,与 轴相交于点 ,连接 、 .
(3)、当半圆 与 无交点时,直接写出 的取值范围.26. 如图,抛物线 经过 , 两点,与 轴相交于点 ,连接 、 . (1)、 与 之间的关系式为:;(2)、判断线段 和 之间的数量关系,并说明理由;(3)、设点 是抛物线 上 、 之间的动点,连接 , ,当 时:
(1)、 与 之间的关系式为:;(2)、判断线段 和 之间的数量关系,并说明理由;(3)、设点 是抛物线 上 、 之间的动点,连接 , ,当 时:①若 ,求点 的坐标;
②若 ,且 的最大值为 ,请直接写出 的值.