河北省承德市2020年中考数学二模试卷
试卷更新日期:2021-03-23 类型:中考模拟
一、单选题
-
1. 《九章算术》中注有“今两算得失相反,要令正负以名之.”意思是:今有两数若其意义相反,则分别叫做正数与负数.若收入120元记作+120,则-40元表示( ).A、收入40元 B、收入80元 C、支出40元 D、支出80元2. 如图,△ABC中,∠C=90°,点D在AC边上,DE∥AB,若∠ADE=46°,则∠B的度数是( )
 A、34° B、44° C、46° D、54°3. 若 用科学记数法表示成 ,则 的相反数为( ).A、5 B、6 C、-5 D、-64. 如果从某一高处甲看低处乙的俯角为30°,那么从乙处看甲处,甲在乙的( )A、俯角30°方向 B、俯角60°方向 C、仰角30°方向 D、仰角60°方向5. 若 ,则( )中的式子是( )A、 B、 C、 D、6. 把边长相等的正五边形ABCDE和正方形ABFG,按照如图所示的方式叠合在一起,连结AD,则∠DAG=( )
A、34° B、44° C、46° D、54°3. 若 用科学记数法表示成 ,则 的相反数为( ).A、5 B、6 C、-5 D、-64. 如果从某一高处甲看低处乙的俯角为30°,那么从乙处看甲处,甲在乙的( )A、俯角30°方向 B、俯角60°方向 C、仰角30°方向 D、仰角60°方向5. 若 ,则( )中的式子是( )A、 B、 C、 D、6. 把边长相等的正五边形ABCDE和正方形ABFG,按照如图所示的方式叠合在一起,连结AD,则∠DAG=( ) A、18° B、20° C、28° D、30°7. 北京海淀区某中学经过食堂装修后重新营业,同学们很高兴品尝各种美食菜品某同学想要得到本校食堂最受同学欢迎的菜品,以下是排乱的统计步骤:
A、18° B、20° C、28° D、30°7. 北京海淀区某中学经过食堂装修后重新营业,同学们很高兴品尝各种美食菜品某同学想要得到本校食堂最受同学欢迎的菜品,以下是排乱的统计步骤:①从扇形图中分析出最受学生欢迎的菜品;
②去食堂收集同学吃饭选择的菜品名称和人数;
③绘制扇形图来表示各个种类产品所占的百分比;
④整理所收集的数据,并绘制频数分布表;
正确统计步骤的顺序是( )
A、②→③→①→④ B、②→④→③→① C、①→②→④→③ D、③→④→①→②8. 已知关于 的一元二次方程 有两个相等的实数根,则下列说法正确的是( )A、1一定不是方程 的根 B、0一定不是方程 的根 C、 可能是方程 的根 D、1和-1都是方程 的根9. 如图, 中, ,将 绕点 按逆时针方向旋转 得到 ,点 在直线 上,若 上,则点 和 外心之间的距离是( ) A、1 B、 C、 D、10. 设函数y= (k≠0,x>0)的图象如图所示,若z= ,则z关于x的函数图象可能为( )
A、1 B、 C、 D、10. 设函数y= (k≠0,x>0)的图象如图所示,若z= ,则z关于x的函数图象可能为( )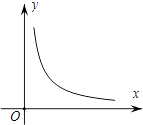 A、
A、 B、
B、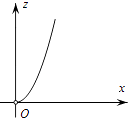 C、
C、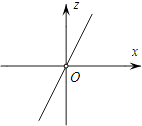 D、
D、 11. 如图,在四边形 中, , ,点 , 分别是 , 边上的点,且 ,DE⊥AB于点 .将 沿 翻折,点 与 恰好重合,则 等于( )
11. 如图,在四边形 中, , ,点 , 分别是 , 边上的点,且 ,DE⊥AB于点 .将 沿 翻折,点 与 恰好重合,则 等于( ) A、4 B、3 C、2 D、112. 由一些大小相等的小正方体组成的几何体的主视图与左视图相同如图所示,设组成这个几何体的小正方体个数最少为m,最多为n,若以m,n的值分别为某个等腰三角形的两条边长,则该等腰三角形的周长为( )
A、4 B、3 C、2 D、112. 由一些大小相等的小正方体组成的几何体的主视图与左视图相同如图所示,设组成这个几何体的小正方体个数最少为m,最多为n,若以m,n的值分别为某个等腰三角形的两条边长,则该等腰三角形的周长为( ) A、11或13 B、13或14 C、13 D、12或13或14或1513. 如图,点 , , 在一次函数 的图象上,它们的横坐标依次为-1,1,2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积和是( )
A、11或13 B、13或14 C、13 D、12或13或14或1513. 如图,点 , , 在一次函数 的图象上,它们的横坐标依次为-1,1,2,分别过这些点作x轴与y轴的垂线,则图中阴影部分的面积和是( ) A、1 B、3 C、 D、14. 如图,已知平行四边形 , ,依下列步骤作图,并保留作图痕迹:
A、1 B、3 C、 D、14. 如图,已知平行四边形 , ,依下列步骤作图,并保留作图痕迹:步骤1:以 为圆心, 长为半径画弧①,分别交 , 于点 , ;
步骤2:以 为圆心,以 长为半径画弧②,交 于点 ;
步骤3:以 为圆心,以 长为半径画弧③,弧②和弧③交于点 ,过 作射线,交 于点 .则下列叙述错误的是:( )
 A、 B、 C、 平分 D、15. 木工师傅要把一根质地均匀的圆柱形木料锯成若干段,按着如图的方式锯开,每锯一次所用的时间均相同.若锯成 ( ,且 为整数)段需要时间是 分,则锯成 段,需要的时间是( ).
A、 B、 C、 平分 D、15. 木工师傅要把一根质地均匀的圆柱形木料锯成若干段,按着如图的方式锯开,每锯一次所用的时间均相同.若锯成 ( ,且 为整数)段需要时间是 分,则锯成 段,需要的时间是( ). A、 分 B、 分 C、 分 D、 分16. 如图, 中, , , ,将半径是1的 沿三角形的内部边缘无滑动的滚动一周,回到起始的位置,则点 所经过的路线长是( )
A、 分 B、 分 C、 分 D、 分16. 如图, 中, , , ,将半径是1的 沿三角形的内部边缘无滑动的滚动一周,回到起始的位置,则点 所经过的路线长是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
17. 若 , , ,则x+y+z= .18. 定义:若 ,则称 与 是关于1的平衡数.(1)、4-x与是关于1的平衡数.(用含 的代数式表示);(2)、若 关于1的平衡数是-7,则x的值为 .19. 如图1,在 内部任取一点 ,则图中互不重叠的所有角的和是
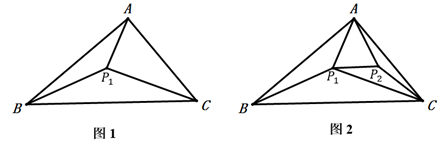 (1)、在图1中的任一小三角形内任取一点 (如图2),则图中互补重叠的所有角的和是;(2)、以此类推,当取到点 时,图中互不重叠的所有角的和是(用含 的代数式表示).
(1)、在图1中的任一小三角形内任取一点 (如图2),则图中互补重叠的所有角的和是;(2)、以此类推,当取到点 时,图中互不重叠的所有角的和是(用含 的代数式表示).三、解答题
-
20. 在数学活动课上,李老师设计了一个游戏活动,四名同学分别代表一种运算,四名同学可以任意排列,每次排列代表一种运算顺序,剩余同学中,一名学生负责说一个数,其他同学负责运算,运算结果既对又快者获胜,可以得到一个奖品.
下面我们用四个卡片代表四名同学(如下):
 (1)、列式,并计算:
(1)、列式,并计算:① 经过 , , , 的顺序运算后,结果是多少?
②5经过 , , , 的顺序运算后,结果是多少?
(2)、探究:数 经过 , , , 的顺序运算后,结果是45, 是多少?21. 如图,在正方形 中, 是 边上任意一点(不与点 , 重合), ,垂足为点 ,交 于点 ,交 于点 ,连接 . (1)、① 与 的数量关系是;
(1)、① 与 的数量关系是;②当 为等腰三角形时, ;
(2)、当点 为 的中点时,求证: ;22. 如图,在平面直角坐标系中,点 , , 三点的坐标分别为 , , ,直线 的解析式为: . (1)、当 时,直线 与 轴交于点 ,点 的坐标 , ;(2)、小明认为点 也在直线 上,他的判断是否符合题意,请说明理由;(3)、若线段 与直线 有交点,求 的取值范围.23. 如图,点 在数轴上对应的数为20,以原点 为圆心, 为半径作优弧 ,使点 在点 右下方,且 ,在优弧 上任取一点 ,过点 作直线 的垂线,交数轴于点 ,设 在数轴上对应的数为 ,连接 .
(1)、当 时,直线 与 轴交于点 ,点 的坐标 , ;(2)、小明认为点 也在直线 上,他的判断是否符合题意,请说明理由;(3)、若线段 与直线 有交点,求 的取值范围.23. 如图,点 在数轴上对应的数为20,以原点 为圆心, 为半径作优弧 ,使点 在点 右下方,且 ,在优弧 上任取一点 ,过点 作直线 的垂线,交数轴于点 ,设 在数轴上对应的数为 ,连接 . (1)、若优弧 上一段 的长为 ,求 的度数及x的值;(2)、求 的最小值,并指出此时直线 与 所在圆的位置关系.24. 为了解业余射击队队员的射击成绩,对某次射击比赛中每一名队员的平均成绩(单位:环,环数为整数)进行了统计,分别绘制了如下统计表和如图所示的频数分布直方图,请你根据统计表和频数分布直方图回答下列问题:
(1)、若优弧 上一段 的长为 ,求 的度数及x的值;(2)、求 的最小值,并指出此时直线 与 所在圆的位置关系.24. 为了解业余射击队队员的射击成绩,对某次射击比赛中每一名队员的平均成绩(单位:环,环数为整数)进行了统计,分别绘制了如下统计表和如图所示的频数分布直方图,请你根据统计表和频数分布直方图回答下列问题:平均成绩
0
1
2
3
4
5
6
7
8
9
10
人数
0
1
3
3
6
1
0
 (1)、参加这次射击比赛的队员有多少名?(2)、这次射击比赛平均成绩的中位数落在频数分布直方图的哪个小组内?(3)、这次射击比赛平均成绩的众数落在频数分布直方图的哪个小组内?(4)、若在成绩为8环,9环,10环的队员中随机选一名参加比赛,求选到成绩为9环的队员的概率.25. 某公司生产甲、乙两种产品.已知生产甲种产品每千克的成本费是30元,生产乙种产品每千克的成本费是20元.物价部门规定,这两种产品的销售单价(每千克的售价)之和为80元.经市场调研发现,甲种产品的销售单价为 (元),在公司规定 的范围内,甲种产品的月销售量 (千克)符合 ;乙种产品的月销售量 (千克)与它的销售单价成正比例,当乙产品单价为30元(即: )时,它的月销售量是30千克.(1)、求 与 之间的函数关系式;(2)、公司怎样定价,可使月销售利润最大?最大月销售利润是多少?(销售利润 销售额 生产成本费)(3)、是否月销售额越大月销售利润也越大?请说明理由.26. 如图, 中, , , .点 从点 出发沿折线 以每秒1个单位长的速度向点 匀速运动,点 从点 出发沿 以每秒2个单位长的速度向点 匀速运动,点 , 同时出发,当其中一点到达点 时停止运动,另一点也随之停止.设点 , 运动的时间是 秒( ).
(1)、参加这次射击比赛的队员有多少名?(2)、这次射击比赛平均成绩的中位数落在频数分布直方图的哪个小组内?(3)、这次射击比赛平均成绩的众数落在频数分布直方图的哪个小组内?(4)、若在成绩为8环,9环,10环的队员中随机选一名参加比赛,求选到成绩为9环的队员的概率.25. 某公司生产甲、乙两种产品.已知生产甲种产品每千克的成本费是30元,生产乙种产品每千克的成本费是20元.物价部门规定,这两种产品的销售单价(每千克的售价)之和为80元.经市场调研发现,甲种产品的销售单价为 (元),在公司规定 的范围内,甲种产品的月销售量 (千克)符合 ;乙种产品的月销售量 (千克)与它的销售单价成正比例,当乙产品单价为30元(即: )时,它的月销售量是30千克.(1)、求 与 之间的函数关系式;(2)、公司怎样定价,可使月销售利润最大?最大月销售利润是多少?(销售利润 销售额 生产成本费)(3)、是否月销售额越大月销售利润也越大?请说明理由.26. 如图, 中, , , .点 从点 出发沿折线 以每秒1个单位长的速度向点 匀速运动,点 从点 出发沿 以每秒2个单位长的速度向点 匀速运动,点 , 同时出发,当其中一点到达点 时停止运动,另一点也随之停止.设点 , 运动的时间是 秒( ). (1)、发现:
(1)、发现:;
(2)、当点 , 相遇时,相遇点在哪条边上?并求出此时 的长.(3)、探究:当 时, 的面积为;
(4)、点 , 分别在 , 上时, 的面积能否是 面积的一半?若能,求出 的值;若不能,请说明理由.拓展:当 时,直接写出此时 的值.