北京市燕山区2020年中考数学一模试卷

试卷更新日期：2021-03-23 类型：中考模拟

进入出卷网下载

一、单选题

1. 2020年5月1日起，北京市全面推行生活垃圾分类.下面图标分别为厨余垃圾、可回收物、有害垃圾、其他垃圾，其中不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 为解决延期开学期间全市初高三学生的学习需求，提升学生的实际获得，北京市教委打造了“答疑平台”，全市144000名初高三学生全部纳入在线答疑辅导范围．将144000用科学记数法表示应为（）

A、144×10³ B、14.4×10⁴ C、1.44×10⁵ D、1.44×10⁶

查看试题解析
3. 方程组 ${\begin{array}{l} 2 m - n = - 4 \\ m - 2 n = 1 \end{array}$ 的解为（）

A、 ${\begin{array}{l} m = - 3 \\ n = - 2 \end{array}$ B、 ${\begin{array}{l} m = - 3 \\ n = 2 \end{array}$ C、 ${\begin{array}{l} m = 3 \\ n = - 2 \end{array}$ D、 ${\begin{array}{l} m = 3 \\ n = 2 \end{array}$

查看试题解析
4. 在数轴上，点A，B分别表示实数a，b，将点A向左平移1个单位长度得到点C，若点C，B关于原点O对称，则下列结论正确的是（）

A、a+b＝1 B、a+b＝﹣1 C、a﹣b＝1 D、a﹣b＝﹣1

查看试题解析
5. 若一个凸多边形的内角和为720°，则这个多边形的边数为 $($ 　　 $)$

A、4 B、5 C、6 D、7

查看试题解析
6. 若a+b＝1，则代数式（ $\frac{a^{2}}{b^{2}}$ ﹣1）• $\frac{2 b^{2}}{a - b}$ 的值为（）

A、﹣2 B、﹣1 C、1 D、2

查看试题解析
7. 如图，矩形ABCD中，BC＝2AB，点E在边AD上，EF⊥BD于点F．若EF＝1，则DE的长为（）

A、 $\sqrt{3}$ B、 $\sqrt{5}$ C、2 D、3

查看试题解析

8. 为了解高校学生对5G移动通信网络的消费意愿，从在校大学生中随机抽取了1000人进行调查，下面是大学生用户分类情况统计表和大学生愿意为5G套餐多支付的费用情况统计图（例如，早期体验用户中愿意为5G套餐多支付10元的人数占所有早期体验用户的50%）．

用户分类	人数
A：早期体验用户（目前已升级为5G用户）	260人
B：中期跟随用户（一年内将升级为5G用户）	540人
C：后期用户（一年后才升级为5G用户）	200人

下列推断中，不合理的是（）

A、早期体验用户中，愿意为5G套餐多支付10元，20元，30元的人数依次递减 B、后期用户中，愿意为5G套餐多支付20元的人数最多 C、愿意为5G套餐多支付10元的用户中，中期跟随用户人数最多 D、愿意为5G套餐多支付20元的用户中，后期用户人数最多

查看试题解析

二、填空题

9. 要使分式 $\frac{3}{x - 2}$ 有意义，则 $x$ 的取值范围是.

查看试题解析
10. 下列几何体中，主视图是三角形的是．

查看试题解析
11. 如图，已知▱ABCD，通过测量，计算得▱ABCD的面积约为cm² ．（结果保留一位小数）

查看试题解析
12. 如图，正方形网格中，点A，B，C，D均在格点上，则∠ACD+∠BDC＝°．

查看试题解析
13. 用四个不等式①a＞b，②ab＞b² ， ③a＞0，④b＞0中的两个不等式作为题设，余下的两个不等式中选择一个作为结论，组成一个真命题：．

查看试题解析
14. 如图，在平面直角坐标系xOy中，点A，C分别在x轴，y轴的正半轴上，以OA，OC为边作矩形OABC，双曲线y＝ $\frac{3}{x}$ （x＞0）与BC边交于点E，且CE：EB＝1：2，则矩形OABC的面积为．

查看试题解析

15. 某大学为了解学生在A，B两家餐厅用餐的满意度，从在A，B两家餐厅都用过餐的学生中随机抽取了100人，每人分别对这两家餐厅进行了评分，统计如下：

人数

满意度评分

餐厅

非常满意

较满意

一般

不太满意

非常不满意

合计

100

若小芸要在A，B两家餐厅中选择一家用餐，根据表格中数据，你建议她去餐厅（填A或B），理由是．

查看试题解析

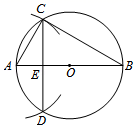
16. 已知⊙O．如图，
⑴作⊙O的直径AB；

⑵以点A为圆心，AO长为半径画弧，交⊙O于C，D两点；

⑶连接CD交AB于点E，连接AC，BC．

根据以上作图过程及所作图形，有下面三个推断：

①CE＝DE； ②BE＝3AE； ③BC＝2CE．

所有正确推断的序号是．

查看试题解析

三、解答题

17. 计算：4sin30°+|﹣ $\sqrt{2}$ |﹣ $\sqrt{8}$ ﹣（ $\frac{1}{2}$ ）^﹣1 ．

查看试题解析
18. 解不等式组： ${\begin{array}{l} 2 (x - 1) \leq x \\ \frac{x - 1}{3} > - 2 \end{array}$ ．

查看试题解析
19. 关于x的方程x²+4x+m+2＝0有两个不相等的实数根，且m为正整数，求m的值及此时方程的根．

查看试题解析
20. 如图，▱ABCD中，点E，F分别在边BC，AD上，BE＝DF，∠AEC＝90°．

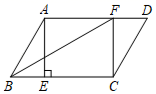(1)、求证：四边形AECF是矩形；

(2)、连接BF，若AB＝4，∠ABC＝60°，BF平分∠ABC，求AD的长．

查看试题解析
21. 抗击新冠肺炎期间，某小区为方便管理，为居民设计了一个身份识别图案系统：在4×4的正方形网格中，白色正方形表示数字1，黑色正方形表示数字0，将第i行第j列表示的数记为a_i_{， j}（其中i，j都是不大于4的正整数），例如，图1中，a₁_{， 2}＝0．对第i行使用公式A_i＝a_i_{， 1}×2³+a_i_{， 2}×2²+a_i_{， 3}×2¹+a_i_{， 4}×2⁰进行计算，所得结果A₁ ， A₂ ， A₃ ， A₄分别表示居民楼号，单元号，楼层和房间号．例如，图1中，A₃＝a₃_{， 1}×2³+a₃_{， 2}×2²+a₃_{， 3}×2¹+a₃_{， 4}×2⁰＝1×8+0×4+0×2+1×1＝9，A₄＝0×8+0×4+1×2+1×1＝3，说明该居民住在9层，3号房间，即903号．

(1)、图1中，a₁_{， 3}＝；

(2)、图1代表的居民居住在号楼单元；

(3)、请仿照图1，在图2中画出8号楼4单元602号居民的身份识别图案．

查看试题解析
22. 如图，AB为⊙O的直径，AC为弦，点D为 $\overset{⌢}{BC}$ 中点，过点D作DE⊥直线AC，垂足为E，交AB的延长线于点F

(1)、求证：EF是⊙O的切线；

(2)、若EF＝4，sin∠F＝ $\frac{3}{5}$ ，求⊙O的半径．

查看试题解析
23. 为了解学生居家学习期间对函数知识的掌握情况，某学校数学教师对九年级全体学生进行了一次摸底测试，测试含一次函数、二次函数和反比例函数三项内容，每项满分10分．现随机抽取20名学生的成绩（成绩均为整数）进行收集、整理、描述和分析，下面给出了部分信息：
a．该20名学生一次函数测试成绩如下：7 9 10 9 7 6 8 10 10 8 6 10 10 9 10 9 9 9 10 10

b．该20名学生总成绩和二次函数测试成绩情况统计图：

c．该20名学生总成绩平均分为25分，一次函数测试平均分为8.8分．

根据以上信息，回答下列问题：

(1)、该20名学生一次函数测试成绩的中位数是，众数是．

(2)、若该校九年级共有400名学生，且总成绩不低于26分的学生成绩记为优秀，估计该校九年级本次测试总成绩优秀的约有人．

(3)、在总成绩和二次函数测试成绩情况统计图中，A同学的一次函数测试成绩是分；若B同学的反比例函数测试成绩是8分，则B同学的一次函数测试成绩是分．

(4)、一次函数、二次函数和反比例函数三项内容中，学生掌握情况最不好的是．

查看试题解析

24. 如图，半圆O的直径AB＝6cm，点M在线段AB上，且BM＝1cm，点P是

\hat{AB}

上的动点，过点A作AN⊥直线PM，垂足为点N．

(1)、小东根据学习函数的经验，对线段AN，MN，PM的长度之间的关系进行了探究．下面是小东的探究过程，请补充完整：
对于点P在

\hat{AB}

上的不同位置，画图、测量，得到了线段AN，MN，PM的长度的几组值，如表：

	位置1	位置2	位置3	位置4	位置5	位置6	位置7
AN/cm	0.00	3.53	4.58	5.00	4.58	4.00	0.00
MN/cm	5.00	3.53	2.00	0.00	2.00	3.00	5.00
PM/cm	1.00	1.23	1.57	2.24	3.18	3.74	5.00

在AN，MN，PM的长度这三个量中，确定的长度是自变量，和的长度都是这个自变量的函数；

(2)、在同一平面直角坐标系xOy中，画出（1）中所确定的函数的图象；

(3)、结合函数图象，解决问题：当AN＝MN时，PM的长度约为cm．

查看试题解析

25. 如图，在平面直角坐标系xOy中，直线l：y＝ $\frac{3}{2}$ x与反比例函数y＝ $\frac{k}{x}$ （x＞0）的图象交于点A(2，a)．

(1)、求a，k的值；

(2)、横，纵坐标都是整数的点叫做整点．点P(m，n)为射线OA上一点，过点P作x轴，y轴的垂线，分别交函数y＝ $\frac{k}{x}$ （x＞0）的图象于点B，C．由线段PB，PC和函数y＝ $\frac{k}{x}$ （x＞0）的图象在点B，C之间的部分所围成的区域（不含边界）记为W．
①若PA＝OA，求区域W内的整点个数；

②若区域W内恰有5个整点，结合函数图象，直接写出m的取值范围．

查看试题解析
26. 在平面直角坐标系xOy中，抛物线y＝ax²+bx﹣3a（a≠0）经过点A(﹣1，0)．

(1)、求抛物线的顶点坐标；（用含a的式子表示）

(2)、已知点B(3，4)，将点B向左平移3个单位长度，得到点C．若抛物线与线段BC恰有一个公共点，结合函数的图象，求a的取值范围．

查看试题解析
27. 如图1，△ABC中，∠ACB＝90°，AC＝BC＝ $\sqrt{2}$ ，M为BC边上的一个动点（不与点B，C重合），连接AM，以点A为中心，将线段AM逆时针旋转135°，得到线段AN，连接BN．

(1)、依题意补全图2；

(2)、求证：∠BAN＝∠AMB；

(3)、点P在线段BC的延长线上，点M关于点P的对称点为Q，写出一个PC的值，使得对于任意的点M，总有AQ＝BN，并证明．

查看试题解析
28. 在平面直角坐标系xOy中，过⊙T（半径为r）外一点P引它的一条切线，切点为Q，若0＜PQ≤2r，则称点P为⊙T的伴随点．

(1)、当⊙O的半径为1时，
①在点A(4，0)，B(0， $\sqrt{5}$ )，C(1， $\sqrt{3}$ )中，⊙O的伴随点是 ▲ ；

②点D在直线y＝x+3上，且点D是⊙O的伴随点，求点D的横坐标d的取值范围；

(2)、⊙M的圆心为M(m，0)，半径为2，直线y＝2x﹣2与x轴，y轴分别交于点E，F．若线段EF上的所有点都是⊙M的伴随点，直接写出m的取值范围．

查看试题解析