北京市西城区2020年中考数学一模试卷
试卷更新日期:2021-03-23 类型:中考模拟
一、单选题
-
1. 北京大兴国际机场目前是全球建设规模最大的机场,2019年,9月25日正式通航,预计到2022年机场旅客吞吐量将达到45 000 000人次,将45 000 000用科学记数法表示为( )A、45× B、4.5× C、4.5× D、0.45×2. 如图是某个几个几何体的三视图,该几何体是( )
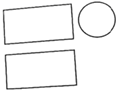 A、圆锥 B、圆柱 C、长方体 D、正三棱柱3. 下面的图形中,既是轴对称图形又是中心对称图形的是( )A、
A、圆锥 B、圆柱 C、长方体 D、正三棱柱3. 下面的图形中,既是轴对称图形又是中心对称图形的是( )A、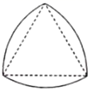 B、
B、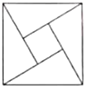 C、
C、 D、
D、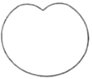 4. 在数轴上,点A,B表示的数互为相反数,若点A在点B的左侧,且AB=2 ,则点A,点B表示的数分别是( )A、- , B、 ,- C、0,2 D、-2 ,25. 如图,AB是⊙O的直径,C,D是⊙O上的两点.若∠CAB= ,则∠ADC的度数为( )
4. 在数轴上,点A,B表示的数互为相反数,若点A在点B的左侧,且AB=2 ,则点A,点B表示的数分别是( )A、- , B、 ,- C、0,2 D、-2 ,25. 如图,AB是⊙O的直径,C,D是⊙O上的两点.若∠CAB= ,则∠ADC的度数为( ) A、 B、 C、 D、6. 甲、乙两名运动员10次射击成绩(单位,环)如图所示.甲、乙两名运动员射击成绩平均数记为 , ,射击成绩的方差依次记为S甲2 , S乙2 , 则下列关系中完全正确的是( )
A、 B、 C、 D、6. 甲、乙两名运动员10次射击成绩(单位,环)如图所示.甲、乙两名运动员射击成绩平均数记为 , ,射击成绩的方差依次记为S甲2 , S乙2 , 则下列关系中完全正确的是( )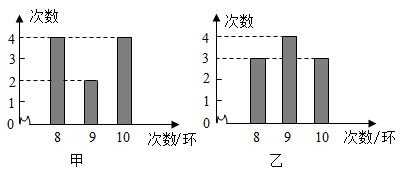 A、 = , S甲2 > B、 = , S甲2 < C、 > , S甲2 > D、 < , S甲2 <7. 如图,在数学实践活动课上,小明同学打算通过测量树的影长计算树的高度,阳光下他测得长1m的竹竿落在地面上的影长为0.9m,在同一时刻测量树的影长时,他发现树的影子有一部分落在地面上,还有一部分落在墙面上,他测得这棵树落在地面上的影长BD为2.7m,落在墙面上的影长CD为1.0m,则这棵树的高度是( )
A、 = , S甲2 > B、 = , S甲2 < C、 > , S甲2 > D、 < , S甲2 <7. 如图,在数学实践活动课上,小明同学打算通过测量树的影长计算树的高度,阳光下他测得长1m的竹竿落在地面上的影长为0.9m,在同一时刻测量树的影长时,他发现树的影子有一部分落在地面上,还有一部分落在墙面上,他测得这棵树落在地面上的影长BD为2.7m,落在墙面上的影长CD为1.0m,则这棵树的高度是( )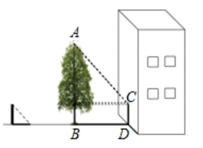 A、6.0m B、5.0m C、4.0m D、3.0m8. 设m是非零实数,给出下列四个命题:①若-1<m<0,则 <m< ;②若m>1,则 < <m;③若m< < ,则m<0;④ <m< ,则0<m<1.其中命题成立的序号是( )A、①③ B、①④ C、②③ D、③④
A、6.0m B、5.0m C、4.0m D、3.0m8. 设m是非零实数,给出下列四个命题:①若-1<m<0,则 <m< ;②若m>1,则 < <m;③若m< < ,则m<0;④ <m< ,则0<m<1.其中命题成立的序号是( )A、①③ B、①④ C、②③ D、③④二、填空题
-
9. 若代数式 在实数范围内有意义,则x的取值范围是。10. 如果一个多边形的内角和等于它的外角和的2倍,那么这个多边形
是 边形.
11. 已知y是以x为自变量的二次函数,且当x=0时,y的最小值为-1,写出一个满足上述条件的二次函数表达式 .12. 如果 ,那么代数式 的值是 .13. 如图,在正方形ABCD中,BE平分∠CBD,EF⊥BD于点F,若DE= ,则BC的长为 .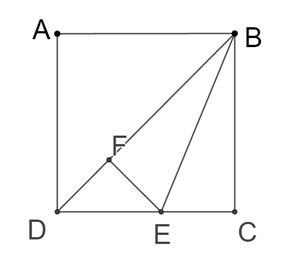 14. 如图,△ABC的顶点A,B,C都在边长为1的正方形网格的格点上,BD⊥AC于点D,则AC的长为 , BD的长为 .
14. 如图,△ABC的顶点A,B,C都在边长为1的正方形网格的格点上,BD⊥AC于点D,则AC的长为 , BD的长为 .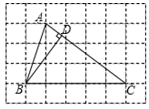 15. 如图,在平面直角坐标系xOy中,点A,B,C的坐标分别是(0,4),(4,0),(8,0),⊙M是△ABC的外接圆,则点M的坐标为.
15. 如图,在平面直角坐标系xOy中,点A,B,C的坐标分别是(0,4),(4,0),(8,0),⊙M是△ABC的外接圆,则点M的坐标为.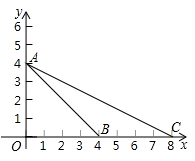 16. 某景区为了解游客人数的变化规律,提高旅游服务质量,收集并整理了某月(30天)接待游客人数(单位:万人)的数据,绘制了下面的统计图和统计表:
16. 某景区为了解游客人数的变化规律,提高旅游服务质量,收集并整理了某月(30天)接待游客人数(单位:万人)的数据,绘制了下面的统计图和统计表: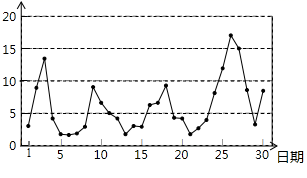
每日接待游客人数(单位∶万人)
游玩环境评价
0≤x <5
好
5Kx <10
一般
10≤x <15
拥挤
15<x <20
严重拥挤
根据以上信息,以下四个判断中,正确的是 . (填写所有符合题意结论的序号)
①该景区这个月游玩环境评价为“拥挤或严重拥挤”的天数仅有4天;
②该景区这个月每日接待游客人数的中位数在5~10广域网人之间;
③该景区这个月平均每日接待游客人数低于5万人;
④这个月1日至5日的五天中,如果某人曾经随机选择其中的两天到该景区游玩,那么他“这两天游玩环境评价均为好”的可能性为 .
三、解答题
-
17. 计算: °.18. 解不等式组 .19. 关于x的一元二次方程 有两个实数根(1)、求m的取值范围;(2)、写出一个满足条件的m的值,求此时方程的根.20. 如图,在 ABCD中,对角线AC,BD交于点O,OA=OB,过点B作BE⊥AC于点E.
 (1)、求证: ABCD是矩形;(2)、若AD= ,cos∠ABE= ,求AC的长.21. 先阅读下列材料,再解答问题.
(1)、求证: ABCD是矩形;(2)、若AD= ,cos∠ABE= ,求AC的长.21. 先阅读下列材料,再解答问题.尺规作图
已知:△ABC,D是边AB上一点,如图1,
求作:四边形DBCF,使得四边形DBCF是平行四边形.
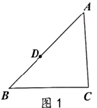
小明的做法如下:
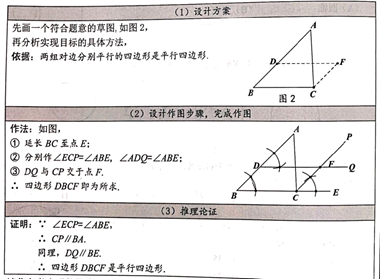
请你参考小明的做法,再设计一一种尺规作图的方法(与小明的方法不同),使得画出的四边形DBCF是平行四边形,并证明.
22. 运用语音识别输入统计可以提高文字输入的速度,为了解A,B两种语音识别输入软件的可读性,小秦同学随机选择了20段话,其中每段话都含有100个字(不计标点符号),在保持相同条件下,标准普通话来测试两种语音识别输入软件的准确性,整个测试分析过程如下,请补充完整.收集数据:两种软件每次识别正确的字数记录如下:

整理,描述数据:根据上面得到的两组样本数据,绘制了分布直方图
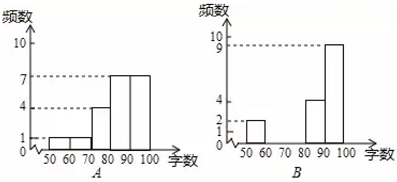
解:统计B组数据得到:60-70的频数为 2,70-80的频数为4,则补全频数分布直方图如图所示:
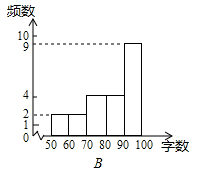 (1)、分析数据:两组样本数据的平均数,众数,中位数,方差如下表所示
(1)、分析数据:两组样本数据的平均数,众数,中位数,方差如下表所示平均数
众数
中位数
方差
A
84.7
84.5
88.91
B
83.7
96
184.01
(2)、得出结论:根据以上信息.判断种语音识别输入软件的准确性较好,理由如下.(至少从两个不同的角度说明判断的合理性) .23. 如图,四边形OABC中, .OA=OC, BA=BC.以O为圆心,以OA为半径作☉O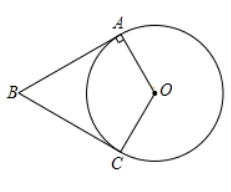 (1)、求证:BC是☉O的切线:(2)、连接BO并延长交⊙O于点D,延长AO交⊙O于点E,与此的延长线交于点F若 .
(1)、求证:BC是☉O的切线:(2)、连接BO并延长交⊙O于点D,延长AO交⊙O于点E,与此的延长线交于点F若 .①补全图形;
②求证:OF=OB.
24. 如图,在△ABC中,AB=4cm.BC=5cm,P是 上的动点.设A,P两点间的距离为xcm,B,P两点间的距离为 cm,C,P两点间的距离为 cm.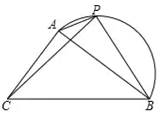
小腾根据学习函数的经验,分别对函数 , 随自变量x的变化而变化的规律进行了探究.
下面是小腾的探究过程,请补充完整:
(1)、按照下表中自变量x的值进行取点、画图、测量,分别得到了 , 的几组对应值:x/cm
0
1
2
3
4
/cm
4.00
3.69
2.13
0
/cm
3.00
3.91
4.71
5.23
5
(2)、在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x, ),(x, ),并画出函数 , 的图象: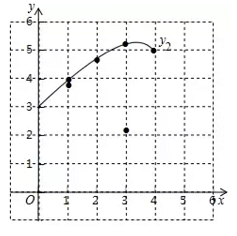 (3)、结合函数图象.
(3)、结合函数图象.①当△PBC为等腰三角形时,AP的长度约为cm.
②记 所在圆的圆心为点O,当直线PC恰好经过点O时,PC的长度约为cm.
25. 在平面直角坐标系xOy中,直线L:y=kx+2k(k>0)与x轴交于点A,与y轴交于点B,与函数 (x>0)的图象的交点P位于第一象限.(1)、若点P的坐标为(1,6),①求m的值及点A的坐标;
② = ▲ ;
(2)、直线h:y=2kx-2与y轴交于点C,与直线L1交于点Q,若点P的横坐标为1,①写出点P的坐标(用含k的式子表示);
②当PQ≤PA时,求m的取值范围.
26. 已知抛物线y=ax2+bx+a+2(a≠0)与x轴交于点A(x1 , 0),点B(x2 , 0),(点A在点B的左侧),抛物线的对称轴为直线x=-1.(1)、若点A的坐标为(-3,0),求抛物线的表达式及点B的坐标;(2)、C是第三象限的点,且点C的横坐标为-2,若抛物线恰好经过点C,直接写出x2的取值范围;(3)、抛物线的对称轴与x轴交于点D,点P在抛物线上,且∠DOP=45°,若抛物线上满足条件的点P恰有4个,结合图象,求a的取值范围.27. 如图,在等腰直角△ABC中,∠ACB=90 点P在线段BC上,延长BC至点Q,使得CQ=CP,连接AP,AQ.过点B作BD⊥AQ于点D,交AP于点E,交AC于点F.K是线段AD上的一个动点(与点A,D不重合),过点K作GN⊥AP于点H,交AB于点G,交AC于点M,交FD的延长线于点N.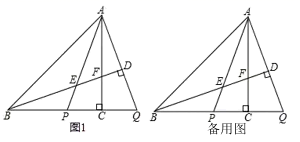 (1)、依题意补全图1;(2)、求证:NM=NF;(3)、若AM=CP,用等式表示线段AE,GN与BN之间的数量关系,并证明.28. 对于平面直角坐标系xOy中的图形W1和图形W2 . 给出如下定义:在图形W1上存在两点A,B(点A,B可以重合),在图形W2上存在两点M,N,(点M于点N可以重合)使得AM=2BN,则称图形W1和图形W2满足限距关系
(1)、依题意补全图1;(2)、求证:NM=NF;(3)、若AM=CP,用等式表示线段AE,GN与BN之间的数量关系,并证明.28. 对于平面直角坐标系xOy中的图形W1和图形W2 . 给出如下定义:在图形W1上存在两点A,B(点A,B可以重合),在图形W2上存在两点M,N,(点M于点N可以重合)使得AM=2BN,则称图形W1和图形W2满足限距关系 (1)、如图1,点C(1,0),D(-1,0),E(0, ),点P在线段DE上运动(点P可以与点D,E重合),连接OP,CP.
(1)、如图1,点C(1,0),D(-1,0),E(0, ),点P在线段DE上运动(点P可以与点D,E重合),连接OP,CP.①线段OP的最小值为 , 最大值为;线段CP的取值范直范围是;
②在点O,点C中,点与线段DE满足限距关系;
(2)、如图2,⊙O的半径为1,直线 (b>0)与x轴、y轴分别交于点F,G.若线段FG与⊙O满足限距关系,求b的取值范围;(3)、⊙O的半径为r(r>0),点H,K是⊙O上的两个点,分别以H,K为圆心,1为半径作圆得到⊙H和¤K,若对于任意点H,K,⊙H和⊙K都满足限距关系,直接写出r的取值范围.