北京市顺义区2020年中考数学一模试卷
试卷更新日期：2021-03-23 类型：中考模拟
一、单选题
-
1. 港珠澳大桥被英国《卫报》誉为“新世界七大奇迹”之一，它是世界总体跨度最长的跨海大桥，全长55000米.数字55000用科学记数法表示为（ ）A、 B、 C、 D、2. 下列有关医疗和倡导卫生的图标中，是轴对称图形的是（ ）A、
B、
C、
D、
3. 将一副三角板按如图所示的位置摆放在直尺上，则∠1的度数为（ ）
A、60° B、65° C、75° D、85°4. 在数轴上，点A表示数a ， 将点A向右平移4个单位长度得到点B ， 点B表示数b ． 若|a|＝|b|，则a的值为（ ）A、﹣3 B、﹣2 C、﹣1 D、15. 箱子内装有除颜色外均相同的28个白球及2个红球，小芬打算从箱子内摸球，以每次摸到一球后记下颜色将球再放回的方式摸28次球．若箱子内每个球被摸到的机会相等，且前27次中摸到白球26次及红球1次，则第28次摸球时，小芬摸到红球的概率是（ ）A、 B、 C、 D、6. 已知直线l及直线l外一点P ． 如图，⑴在直线l上取一点A ， 连接PA；（2）作PA的垂直平分线MN ， 分别交直线l ， PA于点B ， O；（3）以O为圆心，OB长为半径画弧，交直线MN于另一点Q；（4）作直线PQ ． 根据以上作图过程及所作图形，下列结论中错误的是（ ）
A、△OPQ≌△OAB B、PQ∥AB C、AP＝ BQ D、若PQ＝PA ， 则∠APQ＝60°7. 用三个不等式a＞b ， c＞d ， a+c＞b+d中的两个不等式作为题设，余下的一个不等式作为结论组成一个命题，组成真命题的个数为（ ）A、0 B、1 C、2 D、38. 小明、小聪参加了100m跑的5期集训，每期集训结束时进行测试，根据他们的集训时间、测试成绩绘制成如图两个统计图．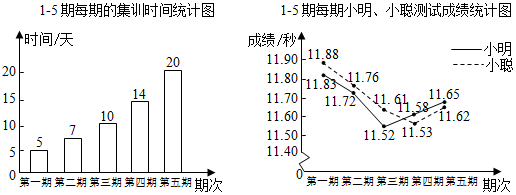
根据图中信息，有下面四个推断：①这5期的集训共有56天；②小明5次测试的平均成绩是11.68秒；③从集训时间看，集训时间不是越多越好，集训时间过长，可能造成劳累，导致成绩下滑；④从测试成绩看，两人的最好成绩都是在第4期出现，建议集训时间定为14天．所有合理推断的序号是（ ）
A、①③ B、②④ C、②③ D、①④二、填空题
-
9. 使得 有意义的 的取值范围是.10. 如图，在量角器的圆心O处下挂一铅锤，制作了一个简易测倾仪．量角器的0刻度线AB对准楼顶时，铅垂线对应的读数是50º，则此时观察楼顶的仰角度数是 ．
11. 在如图所示的几何体中，主视图、左视图和俯视图完全相同的几何体是 ． （写出所有正确答案的序号）
12. 化简分式 的结果为 ．13. 如图，将一矩形纸片ABCD沿着虚线EF剪成两个全等的四边形纸片．根据图中标示的长度与角度，求出剪得的四边形纸片中较短的边AE的长是 ．
14. 已知点A（2，﹣3）关于x轴的对称点A'在反比例函数y＝ 的图象上，则实数k的值为 ．15. 某同学要统计本校图书馆最受学生欢迎的图书种类，以下是打乱顺序的统计步骤：①从扇形图中分析出最受学生欢迎的种类；②去图书馆收集学生借阅图书的记录；③绘制扇形图来表示各个种类所占的百分比；④整理借阅图书记录并绘制频数分布表，正确统计步骤的顺序是 ．
16. 如图，在正方形ABCD中，AB＝4，E、F是对角线AC上的两个动点，且EF＝2，P是正方形四边上的任意一点．若△PEF是等边三角形，则符合条件的P点共有个，此时AE的长为 ．
三、解答题
-
17. 计算：18. 解方程组： ．19. 已知：关于x的方程x2+（m﹣2）x﹣2m＝0．(1)、求证：方程总有实数根；(2)、若方程有一根小于2，求m的取值范围．20. 如图，AM∥BC ， 且AC平分∠BAM ．
(1)、用尺规作∠ABC的平分线BD交AM于点D ， 连接CD ． （只保留作图痕迹，不写作法）(2)、求证：四边形ABCD是菱形．21. 小宜跟几位同学在某快餐厅吃饭，如图为此快餐厅的菜单．若他们所点的餐食总共为10份盖饭，x杯饮料，y份凉拌菜．A套餐：一份盖饭加一杯饮料
B套餐：一份盖饭加一份凉拌菜
C套餐：一份盖饭加一杯饮料与一份凉拌菜
(1)、他们点了份A套餐，份B套餐，份C套餐（均用含x或y的代数式表示）；(2)、若x＝6，且A、B、C套餐均至少点了1份，则最多有种点餐方案．22. 如图，在▱ABCD中，∠B＝45°，点C恰好在以AB为直径的⊙O上．
(1)、求证：CD是⊙O的切线；(2)、连接BD ， 若AB＝8，求BD的长．23. 2019年11月，胡润研究院携手知识产权与科创云平台汇桔，联合发布《IP助燃AI新纪元﹣2019中国人工智能产业知识产权发展白皮书》，白皮书公布了2019中国人工智能企业知识产权竞争力百强榜，对500余家中国人工智能主流企业进行定量评估（满分100分），前三名分别为：华为、腾讯、百度．对得分由高到低的前41家企业的有关数据进行收集、整理、描述和分析．下面给出了部分信息：a ． 得分的频数分布直方图：
（数据分成8组：60≤x＜65，65≤x＜70，70≤x＜75，75≤x＜80，80≤x＜85，85≤x＜90，90≤x＜95，95≤x≤100，）
b ． 知识产权竞争力得分在70≤x＜75这一组的是：70.3，71.6，72.1，72.5，74.1．
c.41家企业注册所在城市分布图（不完整）如图：（结果保留一位小数）
d ． 汉王科技股份有限公司的知识产权竞争力得分是70.3．
（以上数据来源于《IP助燃AI新纪元﹣2019中国人工智能产业知识产权发展白皮书》）
根据以上信息，回答下列问题：
(1)、汉王科技股份有限公司的知识产权竞争力得分排名是第；(2)、百度在人工智能领域取得诸多成果，尤其在智能家居、自动驾驶与服务于企业的智能云领域，百度都已进行前瞻布局，请你估计百度在本次排行榜中的得分大概是；(3)、在41家企业注册所在城市分布图中，m＝ ， 请用阴影标出代表上海的区域；(4)、下列推断合理的是 ． （只填序号）①前41家企业的知识产权竞争力得分的中位数应在65≤x＜70这一组中，众数在65≤x＜70这一组的可能性最大；
②前41家企业分布于我国8个城市．人工智能产业的发展聚集于经济、科技、教育相对发达的城市，一线城市中，北京的优势尤其突出，贡献榜单过半的企业，充分体现北京在人工智能领域的产业集群优势．
24. 如图，D是直径AB上一定点，E ， F分别是AD ， BD的中点，P是 上一动点，连接PA ， PE ， PF ． 已知AB＝6cm ， 设A ， P两点间的距离为xcm ， P ， E两点间的距离为y1cm ， P ， F两点间的距离为y2cm ．
小腾根据学习函数的经验，分别对函数y1 ， y2随自变量x的变化而变化的规律进行了探究．
下面是小腾的探究过程，请补充完整：
(1)、按照下表中自变量x的值进行取点、画图、测量，分别得到了y1 ， y2与x的几组对应值：x/cm
0
1
2
3
4
5
6
y1/cm
0.97
1.27
2.66
3.43
4.22
5.02
y2/cm
3.97
3.93
3.80
3.58
3.25
2.76
2.02
(2)、在同一平面直角坐标系xOy中，描出补全后的表中各组数值所对应的点（x ， y1），（x ， y2），并画出函数y1 ， y2的图象；
(3)、结合函数图象，解决问题：当△PEF为等腰三角形时，AP的长度约为cm ．25. 已知：在平面直角坐标系xOy中，函数y＝ （n≠0，x＞0）的图象过点A（3，2），与直线l：y＝kx+b交于点C ， 直线l与y轴交于点B（0，﹣1）．(1)、求n、b的值；(2)、横、纵坐标都是整数的点叫做整点．记函数y＝ （n≠0，x＞0）的图象在点A ， C之间的部分与线段BA ， BC围成的区域（不含边界）为W ．①当直线l过点（2，0）时，直接写出区域W内的整点个数，并写出区域W内的整点的坐标；
②若区域W内的整点不少于5个，结合函数图象，求k的取值范围．
26. 在平面直角坐标系xOy中，二次函数y＝ax2+bx+c的图象经过点A（0，﹣4）和B（﹣2，2）．(1)、求c的值，并用含a的式子表示b；(2)、当﹣2＜x＜0时，若二次函数满足y随x的增大而减小，求a的取值范围；(3)、直线AB上有一点C（m ， 5），将点C向右平移4个单位长度，得到点D ， 若抛物线与线段CD只有一个公共点，求a的取值范围．27. 已知，如图，△ABC是等边三角形．
(1)、如图1，将线段AC绕点A逆时针旋转90°，得到AD ， 连接BD ， ∠BAC的平分线交BD于点E ， 连接CE ．①求∠AED的度数；
②用等式表示线段AE、CE、BD之间的数量关系（直接写出结果）．
(2)、如图2，将线段AC绕点A顺时针旋转90°，得到AD ， 连接BD ， ∠BAC的平分线交DB的延长线于点E ， 连接CE ．①依题意补全图2；
②用等式表示线段AE、CE、BD之间的数量关系，并证明．
28. 已知：点P为图形M上任意一点，点Q为图形N上任意一点，若点P与点Q之间的距离PQ始终满足PQ＞0，则称图形M与图形N相离．
(1)、已知点A（1，2）、B（0，﹣5）、C（2，﹣1）、D（3，4）．与直线y＝3x﹣5相离的点是；
(2)、若直线y＝3x+b与△ABC相离，求b的取值范围；(3)、设直线y＝ x+3、直线y＝﹣ x+3及直线y＝﹣2围成的图形为W ， ⊙T的半径为1，圆心T的坐标为（t ， 0），直接写出⊙T与图形W相离的t的取值范围．