北京市平谷区2020年中考数学一模试卷

试卷更新日期：2021-03-23 类型：中考模拟

进入出卷网下载

一、单选题

1. 面对突如其来的疫情，全国广大医务工作者以白衣为战袍，义无反顾的冲在抗疫战争的一线，用生命捍卫人民的安全．据统计，全国共有346支医疗队，将近42600名医护工作者加入到支援湖北武汉的抗疫队伍，将42600用科学记数法表示为（）

A、0.426×10⁵ B、4.26×10⁴ C、42.6×10³ D、426×10²

查看试题解析
2. 剪纸是我们国家特别悠久的民间艺术形式之一，它是人们用祥和的图案企望吉祥、幸福的一种寄托．下列剪纸图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. n边形的内角和为1800°，则该n边形的边数为（）

A、12 B、10 C、8 D、6

查看试题解析
4. 若已知实数a ， b满足ab＜0，且a+b＞0，则a ， b在数轴上的位置正确的是（）

A、 B、 C、 D、

查看试题解析
5. 已知锐角∠AOB如图，（1）在射线OA上取一点C ，以点O为圆心，OC长为半径作弧DE ，交射线OB于点F ，连接CF；（2）以点F为圆心，CF长为半径作弧，交弧DE于点G；（3）连接FG ， CG ．作射线OG ．根据以上作图过程及所作图形，下列结论中错误的是（）

A、∠BOG＝∠AOB B、若CG＝OC ，则∠AOB＝30° C、OF垂直平分CG D、CG＝2FG

查看试题解析
6. 如果m﹣n﹣3＝0，那么代数式 $(\frac{m^{2}}{n} - n) \cdot \frac{n}{m + n}$ 的值为（）

A、3 B、2 C、﹣3 D、﹣2

查看试题解析
7. 如图是6×6的正方形网格，点A ， B均在格点上．如果点C也在此正方形网格的格点上，且∠ACB＝90°，则满足条件的点C共有（）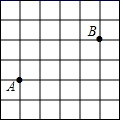

A、3个 B、4个 C、6个 D、8个

查看试题解析
8. 某校在“爱护地球，绿化祖国”的活动中，组织同学开展植树造林活动，为了了解同学的植树情况，学校抽查了初一年级所有同学的植树情况（初一年级共有两个班），并将调查数据整理绘制成如下所示的部分数据尚不完整的统计图表．下面有四个推断：

初一年级植树情况统计表

棵树/棵

1

2

3

4

5

人数

7

33

a

12

3

①a的值为20；②初一年级共有80人；③一班植树棵树的众数是3；④二班植树棵树的是中位数2．其中合理的是（）

A、①③ B、②④ C、②③ D、②③④

查看试题解析

二、填空题

9. 因式分解 $2 x^{2} - 4 x + 2$ = ．

查看试题解析
10. 如图为某几何体的展开图，该几何体的名称是.

查看试题解析
11. 若分式 $\frac{x}{x - 1}$ 有意义，则 $x$ 的取值范围是.

查看试题解析
12. 二次函数y＝ax²+bx+c（0≤x≤3）的图象如图所示，则y的取值范围是．

查看试题解析
13. 用一组a，b的值说明命题“如果 $a > b$ ，那么 $a^{2} > b^{2}$ ”是错误的，这组值可以是.

查看试题解析
14. 如图，矩形ABCD中，AB＝3，BC＝6，点E、F是BC的三等分点，连接AF ， DE ，相交于点M ，则线段ME的长为．

查看试题解析
15. 我国古代数学著作《孙子算经》中记载了这样一个有趣的数学问题“今有五等诸侯，共分橘子60颗，人别加三颗，问五人各得几何？”题目大意是：诸侯5人，共同分60个橘子，若后面的人总比前一个人多分3个，问每个人各分得多少个橘子？若设中间的那个人分得x个，依题意可列方程得．

查看试题解析
16. 某公司计划招募10名技术人员，他们对20名面试合格人员进行了测试，测试包括理论知识和实践操作两部分，20名应聘者的成绩排名情况如图所示，下面有3个推断：
①甲测试成绩非常优秀，入选的可能性很大；

②乙的理论知识排名比实践操作排名靠前；

③位于椭圆形区域内的应聘者应该加强该专业理论知识的学习；

其中合理的是．（写序号）

查看试题解析

三、解答题

17. 计算： $3 \tan 30^{°} - {(π - 4)}^{0} + {(\frac{1}{2})}^{- 1} + | \sqrt{3} - 2 |$

查看试题解析
18. 解不等式组： ${\begin{array}{l} 4 (x - 1) < x + 2 \\ \frac{3 x + 1}{2} > x \end{array}$ ．

查看试题解析
19. 如图，OG平分∠MON ，点A是OM边上一点，过点A作AB⊥OG于点B ， C为线段OA中点，连结BC ．求证：BC∥ON ．

查看试题解析
20. 关于x的一元二次方程x²﹣2kx+k²+k﹣2＝0有两个不相等的实数根．

(1)、求k的取值范围；

(2)、若k为正整数，求k的值及此时方程的根．

查看试题解析
21. 如图，矩形ABCD的对角线AC ， BD相交于点O ，过B点作BF∥AC ，过C点作CF∥BD ， BF与CF相交于点F ．

(1)、求证：四边形BFCO是菱形；

(2)、连接OF、DF ，若AB＝2，tan∠OFD＝ $\frac{2}{3}$ ，求AC的长．

查看试题解析
22. 如图，等边△ABC ，作它的外接圆⊙O ，连接AO并延长交⊙O于点D ，交BC于点E ，过点D作DF∥BC ，交AC的延长线于点F ．

(1)、依题意补全图形并证明：DF与⊙O相切；

(2)、若AB＝6，求CF的长．

查看试题解析
23. 在平面直角坐标系xOy中，反比例函数y＝ $\frac{k}{x}$ （x＞0）的图象G与直线l：y＝2x﹣4交于点A（3，a）．

(1)、求k的值；

(2)、已知点P（0，n）（n＞0），过点P作平行于x轴的直线，与图象G交于点B ，与直线l交于点C ．横、纵坐标都是整数的点叫做整点．记图象G在点A ， B之间的部分与线段AC ， BC围成的区域（不含边界）为W ．
①当n＝5时，直接写出区域W内的整点个数；

②若区域W内的整点恰好为3个，结合函数图象，直接写出n的取值范围．

查看试题解析

24. 2013年11月，习近平同志到湖南湘西考察时，首次作出了“实事求是、因地制宜、分类指导、精准扶贫”的重要指示．精准扶贫一方面要为贫困把脉，找准原因．各省各地区分别对建档立卡的贫困人员进行摸底调查．如图1为某省2013年底，随机抽取40000名建档立卡的贫困人员对他们的致贫原因进行了抽样调查的问卷结果．另一方面，精准扶贫要对症下药，2013至2018年，中央财政安排专项扶贫资金从394亿元增加到1060亿元，累计投入3882亿元；加大贫困地区基础设施建设，进一步完善医疗保险制度；鼓励贫困户自主创业为其优先提供贷款支持．党和人民的共同努力，扶贫工作取得了很大进展，如图2，2013年至2016年，我国现行标准下的农村贫困人口由8249万人减少至4335万人，2018年底，全国贫困人口减至1660万人，贫困发生率从2013年的10.2%降至1.7%．

2013﹣2018全国农村人口总数量统计表（万人）
2013年	2014年	2015年	2016年	2017年	2018年
80872	97458	97808	96333	98258	97647

(1)、补全扇形统计图和条形统计图；

(2)、贫困发生率指的是低于贫困线的人口占该地区全部人口的比例．（贫困发生率＝贫困人数÷统计全人数×100%）．贫困发生率是否低于3%，是判断一个地区是否脱贫的一项重要指标．我国从年开始达到了这个标准；

(3)、结合2013年底的抽样调查结果，下列推断合理的是：．

①生病是导致贫困的最主要原因，因此需要进一步完善医疗保险制度；

②全省约有1800人因贫穷面临辍学；

③通过各地捐款，可以有效缓解了生产资金短缺的困难；

④约有五分之一的贫困人口缺少劳动力和技术支持，我们可以通过实用技术培训，使有劳动能力的贫困人口和有意愿的残疾贫困人口掌握一技之长．

查看试题解析

25. 如图1，P是△ABC外部的一定点，D是线段BC上一动点，连接PD交AC于点E ．

小明根据学习函数的经验，对线段PD ， PE ， CD的长度之间的关系进行了探究，

(1)、下面是小明的探究过程，请补充完整：

对于点D在BC上的不同位置，画图、测量，得到了线段PD ， PE ， CD的长度的几组值，如表：

	位置1	位置2	位置3	位置4	位置5	位置6	位置7	位置8	位置9
PD/cm	2.56	2.43	2.38	2.43	2.67	3.16	3.54	4.45	5.61
PE/cm	2.56	2.01	1.67	1.47	1.34	1.32	1.34	1.40	1.48
CD/cm	0.00	0.45	0.93	1.40	2.11	3.00	3.54	4.68	6.00

在PD ， PE ， CD的长度这三个量中，确定的长度是自变量，的长度和的长度都是这个自变量的函数；

(2)、在同一平面直角坐标系xOy中，画出图2中所确定的两个函数的图象；

(3)、结合函数图象，解决问题：

连接CP ，当△PCD为等腰三角形时，CD的长度约为cm ．（精确到0.1）

查看试题解析

26. 在平面直角坐标系xOy中，二次函数y＝x²﹣2mx+1图象与y轴的交点为A ，将点A向右平移4个单位长度得到点B ．

(1)、直接写出点A与点B的坐标；

(2)、求出抛物线的对称轴（用含m的式子表示）；

(3)、若函数y＝x²﹣2mx+1的图象与线段AB恰有一个公共点，求m的取值范围．

查看试题解析
27. △ABC中，AB＝BC ， ∠ABC＝90°，将线段AB绕点A逆时针旋转α（0°＜α＜90°）得到线段AD ．作射线BD ，点C关于射线BD的对称点为点E ．连接AE ， CE ．

(1)、依题意补全图形；

(2)、若α＝20°，直接写出∠AEC的度数；

(3)、写出一个α的值，使AE＝ $\sqrt{2}$ 时，线段CE的长为 $\sqrt{3}$ ﹣1，并证明．

查看试题解析
28. 在△ABM中，∠ABM＝90°，以AB为一边向△ABM的异侧作正方形ABCD ，以A为圆心，AM为半径作⊙A ，我们称正方形ABCD为⊙A的“关于△ABM的友好正方形”，如果正方形ABCD恰好落在⊙A的内部（或圆上），我们称正方形ABCD为⊙A的“关于△ABM的绝对友好正方形”，例如，图1中正方形ABCD是⊙A的“关于△ABM的友好正方形”．

(1)、图2中，△ABM中，BA＝BM ， ∠ABM＝90°，在图中画出⊙A的“关于△ABM的友好正方形ABCD”．

(2)、若点A在反比例函数y＝ $\frac{k}{x}$ （k＞0，x＞0）上，它的横坐标是2，过点A作AB⊥y轴于B ，若正方形ABCD为⊙A的“关于△ABO的绝对友好正方形”，求k的取值范围．

(3)、若点A是直线y＝﹣x+2上的一个动点，过点A作AB⊥y轴于B ，若正方形ABCD为⊙A的“关于△ABO的绝对友好正方形”，求出点A的横坐标m的取值范围．

查看试题解析

初一年级植树情况统计表
棵树/棵	1	2	3	4	5
人数	7	33	a	12	3