北京市门头沟区2020年中考数学一模试卷

试卷更新日期：2021-03-23 类型：中考模拟

进入出卷网下载

一、单选题

1. 2019年10月1日，庆祝中华人民共和国成立70周年大会在北京天安门广场隆重举行.10月3日微博观看互动量累计达到19280000次，将19280000用科学记数法表示为（）

A、1.928 × 10⁴ B、1928×10⁴ C、1.928 × 10⁷ D、0.1928 × 10⁸

查看试题解析
2. 剪纸艺术是中国古老的民间艺术之一．下列剪纸图案中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 某个几何体的展开图如图所示，该几何体是（）

A、三棱柱 B、三棱锥 C、圆锥 D、圆柱

查看试题解析
4. 如果一个多边形的每一个外角都等于60°，那么这个多边形是（）

A、六边形 B、七边形 C、八边形 D、九边形

查看试题解析
5. 不等式组 ${\begin{array}{l} 2 (x + 3) \geq x + 4, \\ 3 x > 5 x - 4. \end{array}$ 的解集为（）

A、 $- 2 \leq x < 2$ B、 $- 2 < x \leq 2$ C、 $x \geq - 2$ D、 $x > 2$

查看试题解析
6. 点A ， B在数轴上的位置如图所示，如果点C也在数轴上，且B和C两点间的距离是1，那么AC长度为（）

A、2 B、4 C、2或4 D、0或2

查看试题解析
7. 已知，如图，在菱形ABCD中．（1）分别以C ， D为圆心，大于 $\frac{1}{2} C D$ 长为半径作弧，两弧分别交于点E ， F；（2）作直线EF ，且直线EF恰好经过点A ，且与边CD交于点M；（3）连接BM ．根据以上作图过程及所作图形，判断下列结论中错误的是（）

A、∠ABC=60° B、如果AB=2，那么BM=4 C、BC=2CM D、 $S_{△ A B M} = 2 S_{△ A D M}$

查看试题解析
8. 随着智能手机的普及，“支付宝支付”和“微信支付”等手机支付方式倍受广大消费者的青睐，某商场对2019年7−12月中使用这两种手机支付方式的情况进行统计，得到如图所示的折线图，根据统计图中的信息，得出以下四个推断，其中不合理的是（）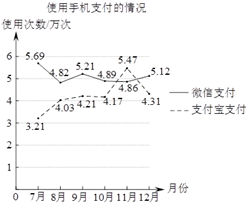

A、6个月中使用“微信支付”的总次数比使用“支付宝支付”的总次数多； B、6个月中使用“微信支付”的消费总额比使用“支付宝支付”的消费总额大； C、6个月中11月份使用手机支付的总次数最多； D、9月份平均每天使用手机支付的次数比12月份平均每天使用手机支付的次数多；

查看试题解析

二、填空题

9. 若式子 $\sqrt{x - 2}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
10. 如图所示的网格是正方形网格，点A ， B ， C是网格线交点，那么 $∠ C A B$ $∠ C B A$ （填“＞”“＜”或“＝”）．

查看试题解析
11. 在数学证明中，当证明一个命题是假命题时，常常采用举反例的办法．如果用一组a ， b的值说明命题“如果 $a > b$ ，那么 $a b > b^{2}$ ”是错误的，那么这样的一组值中，a = ， b = ．

查看试题解析
12. 小明先将图1中的矩形沿虚线剪开分成四个全等的小矩形，再将这四个小矩形拼成如图2的正方形，那么图1中矩形的面积为．

查看试题解析
13. 若一次函数的图象过点（0，2），且函数y随自变量x的增大而增大，请写出一个符合要求的一次函数表达式：．

查看试题解析

14. 抗击肺炎期间，小明准备借助网络评价选取一家店铺，购置防护用品．他先后选取三家店铺，对每家店铺随机选取了1000条网络评价，统计结果如下：

	一星	二星	三星	四星	五星	合计
甲	93	30	54	338	485	1000
乙	80	56	69	340	455	1000
丙	92	128	125	155	500	1000

小明选择在（填“甲”“乙”“丙”）店铺购买防护用品，能获得良好的购物体验（即评价不低于四星）的可能性最大．

查看试题解析

15. 如图，直线 $l_{1} ⊥ l_{2}$ ，在某平面直角坐标系中，x轴∥ $l_{1}$ ，y轴∥ $l_{2}$ ，点A的坐标为( $- 1$ ，2)，点B的坐标为(2， $- 1$ )，那么点C在第象限．

查看试题解析
16. 如图，在平面直角坐标系xOy中，B（3，0），△AOB是等边三角形，动点P从点B出发以每秒1个单位长度的速度沿BO匀速运动，动点Q同时从点A出发以同样的速度沿OA延长线方向匀速运动，当点P到达点O时，点P ， Q同时停止运动．过点P作PE⊥AB于E ，连接PQ交AB于D ．设运动时间为t秒，得出下面三个结论，① 当t =1时，△OPQ为直角三角形；② 当t =2时，以AQ ， AE为边的平行四边形的第四个顶点在∠AOB的平分线上；③ 当t为任意值时， $D E = \frac{1}{2} A B$ ．所有正确结论的序号是．

查看试题解析

三、解答题

17. 计算： $| - \sqrt{3} | - {(π - 2020)}^{0} - 2 \sin 60 ° + {(\frac{1}{3})}^{- 1}$ ．

查看试题解析
18. 已知 $a \neq 0$ ， $a + b \neq 0$ 且 $a - b = 1$ ，求代数式 $\frac{a^{2} - b^{2}}{2 a^{2} + 2 a b} \div (a - \frac{2 a b - b^{2}}{a})$ 的值.

查看试题解析
19. 已知关于x的一元二次方程 $x^{2} - 3 x + (m + 1) = 0$ 有两个不相等的实数根．

(1)、求m的取值范围；

(2)、如果m是非负整数，且该方程的根是整数，求m的值．

查看试题解析
20. 如图，在Rt△ABC中，∠ACB=90°，CD⊥AB于D ， CE∥AB ， EB∥CD ，连接DE交BC于点O ．

(1)、求证：DE=BC；

(2)、如果AC=5， $\tan ∠ A C D = \frac{1}{2}$ ，求DE的长．

查看试题解析
21. 在推进城乡生活垃圾分类的行动中，为了了解社区居民对垃圾分类知识的掌握情况，某社区随机抽取40名居民进行测试，并对他们的得分数据进行收集、整理、描述和分析．下面给出了部分信息：
a ．社区40名居民得分的频数分布直方图：(数据分成5组：50≤x＜60，60≤x＜70，70≤x＜80，80≤x＜90，90≤x＜100)：

b ．社区居民得分在80≤x＜90这一组的是：

80 80 81 82 83 84 84 85 85 85 86 86 87 89

c.40个社区居民的年龄和垃圾分类知识得分情况统计图：

d ．社区居民甲的垃圾分类知识得分为89分．

根据以上信息，回答下列问题：

(1)、社区居民甲的得分在抽取的40名居民得分中从高到低排名第；

(2)、在垃圾分类得分比居民甲得分高的居民中，居民年龄最大约是岁；

(3)、下列推断合理的是．
①相比于点A所代表的社区居民，居民甲的得分略高一些，说明青年人比老年人垃圾分类知识掌握得更好一些；

②垃圾分类知识得分在90分以上的社区居民年龄主要集中在15岁到35岁之间，说明青年人垃圾分类知识掌握更为全面，他们可以向身边的老年人多宣传垃圾分类知识．

查看试题解析
22. 如图，∠APB ，点C在射线PB上，PC为⊙O的直径，在∠APB内部且到∠APB两边距离都相等的所有的点组成图形M ，图形M交⊙O于D ，过点D作直线DE⊥PA ，分别交射线PA ， PB于E ， F ．

(1)、根据题意补全图形；

(2)、求证：DE是⊙O的切线；

(3)、如果PC=2CF ，且 $D F = \sqrt{3}$ ，求PE的长．

查看试题解析

23. 疫情期间，甲、乙、丙、丁4名同学约定周一至周五每天做一组俯卧撑．为了增加趣味性，他们通过游戏方式确定每个人每天的训练计划．

首先，按如图方式摆放五张卡片，正面标有不同的数字代表每天做俯卧撑的个数，反面标有 $x_{1}$ ， $x_{2}$ ， $x_{3}$ ， $x_{4}$ ， $x_{5}$ 便于记录．

具体游戏规则如下：

甲同学：同时翻开 $x_{1}$ ， $x_{2}$ ，将两个数字进行比较，然后由小到大记录在表格中， $x_{3}$ ， $x_{4}$ ， $x_{5}$ 按原顺序记录在表格中；

乙同学：同时翻开 $x_{1}$ ， $x_{2}$ ， $x_{3}$ ，将三个数字进行比较，然后由小到大记录在表格中， $x_{4}$ ， $x_{5}$ 按原顺序记录在表格中；

以此类推，到丁同学时，五张卡片全部翻开，并由小到大记录在表格中．

下表记录的是这四名同学五天的训练计划：

	星期一	星期二	星期三	星期四	星期五
甲同学	$x_{2}$	$x_{1}$	$x_{3}$	$x_{4}$	$x_{5}$
乙同学	$x_{2}$	$x_{3}$	$x_{1}$	$x_{4}$	$x_{5}$
丙同学
丁同学	$x_{4}$	$x_{5}$	$x_{2}$	$x_{3}$	$x_{1}$

根据记录结果解决问题：

(1)、补全上表中丙同学的训练计划；

(2)、已知每名同学每天至少做30个，五天最多做180个．

①如果 $x_{2} = 36$ ， $x_{3} = 40$ ，那么 $x_{1}$ 所有可能取值为；

②这四名同学星期做俯卧撑的总个数最多，总个数最多为个．

查看试题解析

24. 如图，点M是⊙O直径AB上一定点，点C是直径AB上一个动点，过点

C

作

C D ⊥ A B

交⊙O于点

D

，作射线DM交⊙O于点N ，连接BD ．

(1)、小勇根据学习函数的经验，对线段AC ， BD ， MN的长度之间的数量关系进行了探究．

下面是小勇的探究过程，请补充完整：

对于点C在AB的不同位置，画图，测量，得到了线段AC ， BD ， MN的长度的几组值，如下表：

	位置1	位置2	位置3	位置4	位置5	位置6	位置7
AC/cm	0.00	1.00	2.00	3.00	4.00	5.00	6.00
BD/cm	6.00	5.48	4.90	4.24	3.46	2.45	0.00
MN/cm	4.00	3.27	2.83	2.53	2.31	2.14	2.00

在AC ， BD ， MN的长度这三个量中，如果选择的长度为自变量，那么的长度和的长度为这个自变量的函数；

(2)、在同一平面直角坐标系xOy中，画出（1）中确定的函数的图象；

(3)、结合函数图象解决问题：当BD=MN时，线段AC的长度约为cm（结果精确到0.1）．

查看试题解析

25. 在平面直角坐标系xOy中，一次函数 $y = x + m (m \neq 0)$ 的图象与y轴交于点A ，过点 $B (0 ， 2 m)$ ，且平行于x轴的直线与一次函数 $y = x + m (m \neq 0)$ 的图象，反比例函数 $y = \frac{4 m}{x}$ 的图象分别交于点C ， D ．

(1)、求点D 的坐标（用含m的代数式表示）；

(2)、当m = 1时，用等式表示线段BD与CD长度之间的数量关系，并说明理由；

(3)、当BD≤CD时，直接写出m的取值范围．

查看试题解析
26. 在平面直角坐标系xOy中，一次函数 $y = - a x + 3$ 的图象与y轴交于点A ，与抛物线 $y = a x^{2} - 2 a x - 3 a (a \neq 0)$ 的对称轴交于点B ，将点A向右平移5个单位得到点C ，连接AB ， AC得到的折线段记为图形G ．

(1)、求出抛物线的对称轴和点C坐标；

(2)、①当 $a = - 1$ 时，直接写出抛物线 $y = a x^{2} - 2 a x - 3 a$ 与图形G的公共点个数．
②如果抛物线 $y = a x^{2} - 2 a x - 3 a$ 与图形G有且只有一个公共点，求出a的取值范围．

查看试题解析
27. 在△ABC中，∠ACB=90°，∠CAB=30°，点D在AB上，连接CD ，并将CD绕点D逆时针旋转60°得到DE ，连接AE ．

(1)、如图1，当点D为AB中点时，直接写出DE与AE长度之间的数量关系；

(2)、如图2，当点D在线段AB上时，
① 根据题意补全图2；

② 猜想DE与AE长度之间的数量关系，并证明．

查看试题解析
28. 对于平面直角坐标系xOy中的任意点 $P (x ， y)$ ，如果满足 $x + y = a$ (x≥0，a为常数)，那么我们称这样的点叫做“特征点”．

(1)、当2≤a≤3时，
①在点 $A (1 ， 2) ， B (1 ， 3) ， C (2.5 ， 0)$ 中，满足此条件的特征点为；

②⊙W的圆心为 $W (m ， 0)$ ，半径为1，如果⊙W上始终存在满足条件的特征点，请画出示意图，并直接写出m的取值范围；

(2)、已知函数 $Z = \frac{1}{x} + x (x > 0)$ ，请利用特征点求出该函数的最小值．

查看试题解析