北京市海淀区2020年中考数学一模试卷
试卷更新日期：2021-03-23 类型：中考模拟
一、单选题
-
1. -2的相反数是（ ）A、2 B、-2 C、 D、2. 下列几何体中，主视图为矩形的是（ ）A、
B、
C、
D、
3. 北京故宫有着近六百年的历史，是最受中外游客喜爱的景点之一，其年接待量在2019年首次突破19000000人次大关．将19000000用科学记数法可表示为（ ）A、0.19×108 B、0.19×107 C、1.9×107 D、19×1064. 北京大兴国际机场于2019年6月30日完美竣工，如图是世界著名建筑设计大师扎哈设计的机场成体俯视图的示意图．下列说法正确的是（ ）
A、这个图形是轴对称图形，但不是中心对称图形 B、这个图形是中心对称图形，但不是轴对称图形 C、这个图形既是轴对称图形，又是中心对称图形 D、这个图形既不是轴对称图形，也不是中心对称图形5. 将抛物线y＝2x2向下平移3个单位长度所得到的抛物线是（ ）A、y＝2x2+3 B、y＝2x2﹣3 C、y＝2（x﹣3）2 D、y＝2（x+3）26. 如图，AB与⊙O相切于点B ， AO的延长线交⊙O于点C ， 连结BC ， 若OC= OA ， 则∠C等于（ ）
A、15° B、30° C、45° D、60°7. 若实数m ， n ， p ， q在数轴上的对应点的位置如图所示，且n与q互为相反数，则绝对值最大的数对应的点是（ ）
A、点M B、点N C、点P D、点Q8. 如图，在平面直角坐标系xOy中，AB ， CD ， EF ， GH是正方形OPQR边上的线段，点M在其中某条线段上，若射线OM与x轴正半轴的夹角为α，且sinα＞cosα，则点M所在的线段可以是（ ）
A、AB和CD B、AB和EF C、CD和GH D、EF和GH二、填空题
-
9. 若代数式 在实数范围内有意义，则x的取值范围是。10. 如图，在Rt△ABC中，∠C=90°，BC=2，且tanA= ，则AC= ．
11. 分解因式： =.12. 若一个多边形的每一个外角都等于40°，则这个多边形的边数是 ．13. 某校初三年级在“停课不停学”期间，积极开展网上答疑活动，在某时间段共开放7个网络教室，其中4个是数学答疑教室，3个是语文答疑教室．为了解初三年级学生的答疑情况，学校教学管理人员随机进入一个网络教室，则该教室是数学答疑教室的概率为 ．14. 如图，在▱ABCD中，延长CD至点E ， 使DE=DC ， 连接BE与AC于点F ， 则 的值是 ．
15. 为了丰富同学们的课余生活，某年级买了3个篮球和2个足球，共花费了474元，其中篮球的单价比足球的单价多8元，求篮球和足球的单价，如果设篮球的单价为x元，足球的单价为y元，依题意可列方程组为 ．16. 如果四边形有一组对边平行，且另一组对边不平行，那么称这样的四边形为梯形，若梯形中有一个角是直角，则称其为直角梯形．下面四个结论中：①存在无数个直角梯形，其四个顶点分别在同一个正方形的四条边上；
②存在无数个直角梯形，其四个顶点在同一条抛物线上；
③存在无数个直角梯形，其四个顶点在同一个反比例函数的图象上；
④至少存在一个直角梯形，其四个顶点在同一个圆上．
所有正确结论的序号是 ．
三、解答题
-
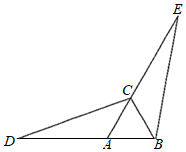
17. 计算： ．18. 解不等式组： ．19. 如图，已知等边三角形ABC ， 延长BA至点D ， 延长AC至点E ， 使AD=CE ， 连接CD ， BE ． 求证：△ACD≌△CBE ．
20. 已知关于x的一元二次方程x2﹣2x+2m﹣1=0.(1)、当m=﹣1时，求此方程的根；(2)、若此方程有两个实数根，求m的取值范围.21. 如图，在▱ABCD中，∠ABC=60°，∠BAD的平分线交CD于点E ， 交BC的延长线于点F ， 连接DF ．
(1)、求证：△ABF是等边三角形；(2)、若∠CDF=45°，CF=2，求AB的长度．22. 致敬，最美逆行者!病毒虽无情，人间有大爱，2020年，在湖北省抗击新冠病毒的战“疫”中，全国（除湖北省外）共有30个省（区、市）及军队的医务人员在党中央全面部署下，白衣执甲，前赴后继支援湖北省抗击疫情，据国家卫健委的统计数据，截至3月1日，这30个省（区、市）累计派出医务人员总数多达38478人，其中派往湖北省除武汉外的其他地区的医务人员总数为7381人．
a ． 全国30个省（区、市）各派出支援武汉的医务人员频数分布直方图
（数据分成6组：100≤x＜500，500≤x＜900，900≤x＜1300，1300≤x＜1700，1700≤x＜2100，2100≤x＜2500）：
b ． 全国30个省（区、市）各派出支援武汉的医务人员人数在900≤x＜1300这一组的是：
919，997，1045，1068，1101，1159，1179，1194，1195，1262．
根据以上信息回答问题：
(1)、这次支援湖北省抗疫中，全国30个省（区、市）派往武汉的医务人员总数A ． 不到3万人，B ． 在3万人到3.5万人之间，C ． 超过3.5万人
(2)、全国30个省（区、市）各派出支援武汉的医务人员人数的中位数是 ， 其中医务人员人数超过1000人的省（区、市）共有个．(3)、据新华网报道，在支援湖北省的医务人员大军中，有“90后”也有“00后”，他们是青春的力量，时代的脊梁．习近平总书记回信勉励北京大学援鄂医疗队全体“90后”党员中指出：“在新冠肺炎疫情防控斗争中，你们青年人同在一线英勇奋战的广大疫情防控人员一道，不畏艰险、冲锋在前、舍生忘死，澎显了青春的蓬勃力量，交出了合格答卷．”小华在收集支援湖北省抗疫宣传资料时得到这样一组有关“90后”医务人员的数据：
C市派出的1614名医护人员中有404人是“90后”；
H市派出的338名医护人员中有103人是“90后”；
B市某医院派出的148名医护人员中有83人是“90后”．
小华还了解到除全国30个省（区、市）派出38478名医务人员外，军队派出了近四千名医务人员，合计约4.2万人．请你根据小华得到的这些数据估计在支援湖北省的全体医务人员（按4.2万人计）中，“90后”大约有多少万人？（写出计算过程，结果精确到0.1）．
23. 在平面直角坐标系xOy中，直线x=3与直线y= x+1交于点A ， 函数y= （k＞0，x＞0）的图象与直线x=3，直线y= x+1分别交于点B ， C ．
(1)、求点A的坐标．(2)、横、纵坐标都是整数的点叫做整点．记函数y= （k＞0，x＞0）的图象在点B ， C之间的部分与线段AB ， AC围成的区域（不含边界）为W ．①当k=1时，结合函数图象，求区域W内整点的个数；
②若区域W内恰有1个整点，直接写出k的取值范围．
24. 如图，在Rt△ABC中，∠BAC=90°，点D为BC边的中点，以AD为直径作⊙O ， 分别与AB ， AC交于点E ， F ， 过点E作EG⊥BC于G ．
(1)、求证：EG是⊙O的切线；(2)、若AF=6，⊙O的半径为5，求BE的长．25. 某校举办球赛，分为若干组，其中第一组有A ， B ， C ， D ， E五个队．这五个队要进行单循环赛，即每两个队之间要进行一场比赛，每场比赛采用三局两胜制，即三局中胜两局就获胜．每场比赛胜负双方根据比分会获得相应的积分，积分均为正整数．这五个队完成所有比赛后得到如下的积分表．
根据上表回答下列问题：
(1)、第一组一共进行了场比赛，A队的获胜场数x为；(2)、当B队的总积分y=6时，上表中m处应填 ， n处应填；(3)、写出C队总积分p的所有可能值为： ．26. 在平面直角坐标系 中，抛物线 的顶点为(1)、求抛物线的顶点坐标（用 表示）；(2)、若点 在第一象限，且 ，求抛物线的解析式；(3)、已知点 ， ，若抛物线与线段 有公共点，结合函数图象，直接写出 的取值范围27. 已知∠MON=α，A为射线OM上一定点，OA=5，B为射线ON上一动点，连接AB ， 满足∠OAB ， ∠OBA均为锐角．点C在线段OB上（与点O ， B不重合），满足AC=AB ， 点C关于直线OM的对称点为D ， 连接AD ， OD ．
(1)、依题意补全图1；(2)、求∠BAD的度数（用含α的代数式表示）；(3)、若tanα= ，点P在OA的延长线上，满足AP=OC ， 连接BP ， 写出一个AB的值，使得BP∥OD ， 并证明．28. A ， B是⊙C上的两个点，点P在⊙C的内部．若∠APB为直角，则称∠APB为AB关于⊙C的内直角，特别地，当圆心C在∠APB边（含顶点）上时，称∠APB为AB关于⊙C的最佳内直角．如图1，∠AMB是AB关于⊙C的内直角，∠ANB是AB关于⊙C的最佳内直角．在平面直角坐标系xOy中．
(1)、如图2，⊙O的半径为5，A（0，﹣5），B（4，3）是⊙O上两点．①已知P1（1，0），P2（0，3），P3（﹣2，1），在∠AP1B ， ∠AP2B ， ∠AP3B ， 中，是AB关于⊙O的内直角的是；
②若在直线y=2x+b上存在一点P ， 使得∠APB是AB关于⊙O的内直角，求b的取值范围 ．
(2)、点E是以T（t ， 0）为圆心，4为半径的圆上一个动点，⊙T与x轴交于点D（点D在点T的右边）．现有点M（1，0），N（0，n），对于线段MN上每一点H ， 都存在点T ， 使∠DHE是DE关于⊙T的最佳内直角，请直接写出n的最大值，以及n取得最大值时t的取值范围．