北京市房山区2020年中考数学一模试卷
试卷更新日期:2021-03-23 类型:中考模拟
一、单选题
-
1. 2019年9月25日正式通航的北京大兴国际机场,为4F级国际机场、大型国际枢纽机场.距北京大兴国际机场官方微博显示,2019年北京大兴国际机场共完成旅客吞吐量313.82万人次,保障航班约21000架次,货邮吞吐量7375.53吨,航班放行正点率达96%以上.将21000用科学记数法表示应为( )A、2.1×104 B、21×103 C、0.21×105 D、2.1×1032. 一副直角三角板有不同的摆放方式,图中满足∠α与∠β相等的摆放方式是( )A、
 B、
B、 C、
C、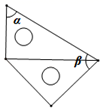 D、
D、 3. 实数a、b、c、d在数轴上对应点的位置如图所示,正确的结论有( )
3. 实数a、b、c、d在数轴上对应点的位置如图所示,正确的结论有( ) A、a>b B、bc>0 C、|c|>|b| D、b+d>04. 下列四种网络运营商的徽标中,符合轴对称图形特征的为( )A、
A、a>b B、bc>0 C、|c|>|b| D、b+d>04. 下列四种网络运营商的徽标中,符合轴对称图形特征的为( )A、 B、
B、 C、
C、 D、
D、 5. 如果a﹣b=5,那么代数式( ﹣2)• 的值是( )A、﹣ B、 C、﹣5 D、56. 一个多边形的每个内角都等于120°, 则此多边形是( )A、五边形 B、七边形 C、六边形 D、八边形7. 某景区乘坐缆车观光游览的价目表如下:
5. 如果a﹣b=5,那么代数式( ﹣2)• 的值是( )A、﹣ B、 C、﹣5 D、56. 一个多边形的每个内角都等于120°, 则此多边形是( )A、五边形 B、七边形 C、六边形 D、八边形7. 某景区乘坐缆车观光游览的价目表如下:缆车类型
两人车(限乘2人)
四人车(限乘4人)
六人车(限乘6人)
往返费用
80元
120元
150元
某班20名同学一起来该景区游玩,都想坐缆车观光游览,且每辆缆车必须坐满,那么他们的费用最低为( )
A、530元 B、540元 C、580元 D、590元8. 已知关于n的函数s=an2+bn(n为自然数),当n=9时,s<0;当n=10时,s>0.则n取( )时,s的值最小.A、3 B、4 C、5 D、6二、填空题
-
9. 若二次根式 有意义,则x的取值范围是 .10. 分解因式: =11. 举出一个m的值,说明命题“代数式2m2﹣1的值一定大于代数式m2﹣1的值”是错误的,那么这个m的值可以是 .12. 如图所示的网格是正方形网格,则∠PAB﹣∠PCD=°.(点A,B,C,D,P是网格线交点)
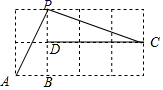 13. 明代的程大位创作了《算法统宗》,它是一本通俗实用的数学书,将枯燥的数学问题化成了美妙的诗歌,读来朗朗上口,是将数字入诗的代表作.其中有一首饮酒数学诗:“肆中饮客乱纷纷,薄酒名醨厚酒醇.醇酒一瓶醉三客,薄酒三瓶醉一人,共同饮了一十九,三十三客醉颜生,试问高明能算士,几多醨酒几多醇?”这首诗是说:“好酒一瓶,可以醉倒3位客人;薄酒三瓶,可以醉倒1位客人,如今33位客人醉倒了,他们总共饮下19瓶酒.试问:其中好酒、薄酒分别是多少瓶?”设有好酒x瓶,薄酒y瓶.根据题意,可列方程组为 .14. 已知第一组数据:12,14,16,18的方差为S12;第二组数据:32,34,36,38的方差为S22;第三组数据:2020,2019,2018,2017的方差为S32 , 则S12 , S22 , S32的大小关系是S12S22S32(填“>”,“=”或“<”).15. 如图,AC是⊙O的弦,AC=6,点B是⊙O上的一个动点,且∠ABC=60°,若点M、N分别是AC、BC的中点,则MN的最大值是 .
13. 明代的程大位创作了《算法统宗》,它是一本通俗实用的数学书,将枯燥的数学问题化成了美妙的诗歌,读来朗朗上口,是将数字入诗的代表作.其中有一首饮酒数学诗:“肆中饮客乱纷纷,薄酒名醨厚酒醇.醇酒一瓶醉三客,薄酒三瓶醉一人,共同饮了一十九,三十三客醉颜生,试问高明能算士,几多醨酒几多醇?”这首诗是说:“好酒一瓶,可以醉倒3位客人;薄酒三瓶,可以醉倒1位客人,如今33位客人醉倒了,他们总共饮下19瓶酒.试问:其中好酒、薄酒分别是多少瓶?”设有好酒x瓶,薄酒y瓶.根据题意,可列方程组为 .14. 已知第一组数据:12,14,16,18的方差为S12;第二组数据:32,34,36,38的方差为S22;第三组数据:2020,2019,2018,2017的方差为S32 , 则S12 , S22 , S32的大小关系是S12S22S32(填“>”,“=”或“<”).15. 如图,AC是⊙O的弦,AC=6,点B是⊙O上的一个动点,且∠ABC=60°,若点M、N分别是AC、BC的中点,则MN的最大值是 .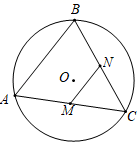 16. ▱ABCD中,对角线AC、BD相交于点O , E是边AB上的一个动点(不与A、B重合),连接EO并延长,交CD于点F , 连接AF , CE , 下列四个结论中:
16. ▱ABCD中,对角线AC、BD相交于点O , E是边AB上的一个动点(不与A、B重合),连接EO并延长,交CD于点F , 连接AF , CE , 下列四个结论中:①对于动点E , 四边形AECF始终是平行四边形;
②若∠ABC<90°,则至少存在一个点E , 使得四边形AECF是矩形;
③若AB>AD , 则至少存在一个点E , 使得四边形AECF是菱形;
④若∠BAC=45°,则至少存在一个点E , 使得四边形AECF是正方形.
以上所有正确说法的序号是 .
三、解答题
-
17. 计算:|﹣ |﹣(π﹣3)0+2cos45°+( )﹣118. 解不等式组:19. 下面是小方设计的“作一个30°角”的尺规作图过程.
已知:直线AB及直线AB外一点P .
求作:直线AB上一点C , 使得∠PCB=30°.
作法:
①在直线AB上取一点M;
②以点P为圆心,PM为半径画弧,与直线AB交于点M、N;
③分别以M、N为圆心,PM为半径画弧,在直线AB下方两弧交于点Q .
④连接PQ , 交AB于点O .
⑤以点P为圆心,PQ为半径画弧,交直线AB于点C且点C在点O的左侧.则∠PCB就是所求作的角.

根据小方设计的尺规作图过程,
(1)、使用直尺和圆规补全图形;(保留作图痕迹)(2)、完成下面的证明.证明:∵PM=PN=QM=QN ,
∴四边形PMQN是 ▲ .
∴PQ⊥MN , PQ=2PO( ▲ ).(填写推理依据)
∵在Rt△POC中,sin∠PCB= = ▲ (填写数值)
∴∠PCB=30°.
20. 已知:关于x的方程x2+4x+2m=0有实数根.(1)、求m的取值范围;(2)、若m为正整数,且该方程的根都是整数,求m的值.21. 在平面直角坐标系xOy中,反比例函数y= 的图象与一次函数y=2x﹣1的图象交于A、B两点,已知A(m , ﹣3).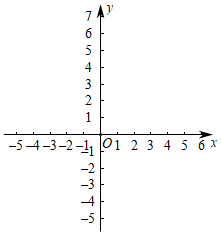 (1)、求k及点B的坐标;(2)、若点C是y轴上一点,且S△ABC=5,直接写出点C的坐标.22. 经过举国上下抗击新型冠状病毒的斗争,疫情得到了有效控制,国内各大企业在2月9日后纷纷进入复工状态.为了了解全国企业整体的复工情况,我们查找了截止到2020年3月1日全国部分省份的复工率,并对数据进行整理、描述和分析.下面给出了一些信息:
(1)、求k及点B的坐标;(2)、若点C是y轴上一点,且S△ABC=5,直接写出点C的坐标.22. 经过举国上下抗击新型冠状病毒的斗争,疫情得到了有效控制,国内各大企业在2月9日后纷纷进入复工状态.为了了解全国企业整体的复工情况,我们查找了截止到2020年3月1日全国部分省份的复工率,并对数据进行整理、描述和分析.下面给出了一些信息: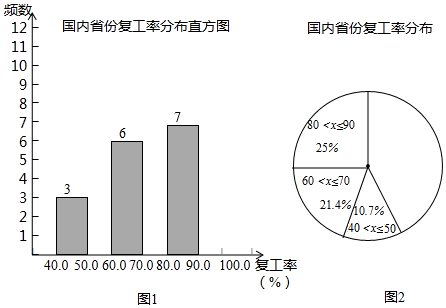
a . 截止3月1日20时,全国已有11个省份工业企业复工率在90%以上,主要位于东南沿海地区,位居前三的分别是贵州(100%)、浙江(99.8%)、江苏(99%).
b . 各省份复工率数据的频数分布直方图如图1(数据分成6组,分别是40<x≤50;
50<x≤60;60<x≤70;70<x≤80;80<x≤90;90<x≤100):
c . 如图2,在b的基础上,画出扇形统计图:
d . 截止到2020年3月1日各省份的复工率在80<x≤90这一组的数据是:
81.3
83.9
84
87.6
89.4
90
90
e . 截止到2020年3月1日各省份的复工率的平均数、中位数、众数如下:
日期
平均数
中位数
众数
截止到2020年3月1日
80.79
m
50,90
请解答以下问题:
(1)、依据题意,补全频数分布直方图;(2)、扇形统计图中50<x≤60这组的圆心角度数是度(精确到0.1).(3)、中位数m的值是 .(4)、根据以上统计图表简述国内企业截止3月1日的复工率分布特征.23. 如图,矩形ABCD , 过点B作BE∥AC交DC的延长线于点E . 过点D作DH⊥BE于H , G为AC中点,连接GH . (1)、求证:BE=AC .(2)、判断GH与BE的数量关系并证明.24. 如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O交AB于点D , 线段BC上有一点P .
(1)、求证:BE=AC .(2)、判断GH与BE的数量关系并证明.24. 如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O交AB于点D , 线段BC上有一点P . (1)、当点P在什么位置时,直线DP与⊙O有且只有一个公共点,补全图形并说明理由.(2)、在(1)的条件下,当BP= ,AD=3时,求⊙O半径.25. 如图1,在弧MN和弦MN所组成的图形中,P是弦MN上一动点,过点P作弦MN的垂线,交弧MN于点Q , 连接MQ . 已知MN=6cm , 设M、P两点间的距离为xcm , P、Q两点间的距离为y1cm , M、Q两点间的距离为y2cm . 小轩根据学习函数的经验,分别对函数y1 , y2随自变量x的变化而变化的规律进行了探究.下面是小轩的探究过程,
(1)、当点P在什么位置时,直线DP与⊙O有且只有一个公共点,补全图形并说明理由.(2)、在(1)的条件下,当BP= ,AD=3时,求⊙O半径.25. 如图1,在弧MN和弦MN所组成的图形中,P是弦MN上一动点,过点P作弦MN的垂线,交弧MN于点Q , 连接MQ . 已知MN=6cm , 设M、P两点间的距离为xcm , P、Q两点间的距离为y1cm , M、Q两点间的距离为y2cm . 小轩根据学习函数的经验,分别对函数y1 , y2随自变量x的变化而变化的规律进行了探究.下面是小轩的探究过程,
请补充完整:
(1)、按照下表中自变量x的值进行取点、画图、测量,分别得到了y1 , y2与x的几组对应值:x/cm .x/cm
0
1
2
3
4
5
6
y1/cm
0
2.24
2.83
3.00
2.83
2.24
0
y2/cm
0
2.45
3.46
4.24
m
5.48
6
上表中m的值为 . (保留两位小数)
(2)、在同一平面直角坐标系xOy(图2)中,函数y1的图象如图,请你描出补全后的表中y2各组数值所对应的点(x , y2),并画出函数y2的图象;(3)、结合函数图象,解决问题:当△MPQ有一个角是30°时,MP的长度约为cm . (保留两位小数)26. 在平面直角坐标系xOy中,已知抛物线y=ax2+bx﹣1交y轴于点P .(1)、过点P作与x轴平行的直线,交抛物线于点Q , PQ=4,求 的值;(2)、横纵坐标都是整数的点叫做整点.在(1)的条件下,记抛物线与x轴所围成的封闭区域(不含边界)为W . 若区域W内恰有4个整点,结合函数图象,求a的取值范围.27. 如图1,在等腰Rt△ABC中,∠BAC=90°,AB=AC=2,点M为BC中点.点P为AB边上一动点,点D为BC边上一动点,连接DP , 以点P为旋转中心,将线段PD逆时针旋转90°,得到线段PE , 连接EC .
 (1)、当点P与点A重合时,如图2.
(1)、当点P与点A重合时,如图2.①根据题意在图2中完成作图;
②判断EC与BC的位置关系并证明.
(2)、连接EM , 写出一个BP的值,使得对于任意的点D总有EM=EC , 并证明.28. 如图,平面上存在点P、点M与线段AB . 若线段AB上存在一点Q , 使得点M在以PQ为直径的圆上,则称点M为点P与线段AB的共圆点.已知点P(0,1),点A(﹣2,﹣1),点B(2,﹣1).
 (1)、在点O(0,0),C(﹣2,1),D(3,0)中,可以成为点P与线段AB的共圆点的是;(2)、点K为x轴上一点,若点K为点P与线段AB的共圆点,请求出点K横坐标xK的取值范围;(3)、已知点M(m , ﹣1),若直线y= x+3上存在点P与线段AM的共圆点,请直接写出m的取值范围.
(1)、在点O(0,0),C(﹣2,1),D(3,0)中,可以成为点P与线段AB的共圆点的是;(2)、点K为x轴上一点,若点K为点P与线段AB的共圆点,请求出点K横坐标xK的取值范围;(3)、已知点M(m , ﹣1),若直线y= x+3上存在点P与线段AM的共圆点,请直接写出m的取值范围.