北京理工附中2020年中考数学4月模拟试卷

试卷更新日期：2021-03-23 类型：中考模拟

进入出卷网下载

一、单选题

1. 若代数式 $\frac{x^{2}}{x - 2}$ 有意义，则实数x的取值范围是（）

A、x＝0 B、x＝2 C、x≠0 D、x≠2

查看试题解析
2. 如图，在△ABC中，过点B作PB⊥BC于B，交AC于P，过点C作CQ⊥AB，交AB延长线于Q，则△ABC的高是（）

A、线段PB B、线段BC C、线段CQ D、线段AQ

查看试题解析
3. 如图，数轴上每相邻两点距离表示1个单位，点A ， B互为相反数，则点C表示的数可能是（）

A、0 B、1 C、3 D、5

查看试题解析
4. 不等式组 ${\begin{matrix} 2 - x > 1 ， ① \\ \frac{x + 5}{2} \geq 1 ， ② \end{matrix}$ 中，不等式①和②的解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
5. 如图，小巷左右两侧是竖直的墙，一架梯子斜靠在左墙时，梯子底端到左墙角的距离为0.7米，顶端距离地面2.4米，如果保持梯子底端位置不动，将梯子斜靠在右墙时，顶端距离地面2米，那么小巷的宽度为（）

A、0.7米 B、1.5米 C、2.2米 D、2.4米

查看试题解析
6. 一个正多边形的每个内角的度数都等于相邻外角的度数，则该正多边形的边数是（）

A、3 B、4 C、6 D、12

查看试题解析
7. “龟兔赛跑”是同学们熟悉的寓言故事.如图所示，表示了寓言中的龟、兔的路程S和时间t的关系（其中直线段表示乌龟，折线段表示兔子）.下列叙述正确的是（）

A、赛跑中，兔子共休息了50分钟 B、乌龟在这次比赛中的平均速度是0.1米/分钟 C、兔子比乌龟早到达终点10分钟 D、乌龟追上兔子用了20分钟

查看试题解析
8. 在平面直角坐标系 $x o y$ 中，函数 $y = \frac{2}{x} (x < 0)$ 的图象与直线 $l_{1}$ ： $y = \frac{1}{3} x + b (b < 0)$ 交于点 $A$ ，与直线 $l_{2}$ ： $x = b$ 交于点 $B$ ，直线 $l_{1}$ 与 $l_{2}$ 交于点 $C$ ，记函数 $y = \frac{2}{x} (x < 0)$ 的图象在点 $A$ 、 $B$ 之间的部分与线段 $A C$ ，线段 $B C$ 围城的区域（不含边界）为 $W$ ，当 $- \frac{4}{3} \leq b \leq - \frac{2}{3}$ 时，区域 $W$ 的整点个数为（）

A、3个 B、2个 C、1个 D、没有

查看试题解析

二、填空题

9. 北京大力拓展绿色生态空间，过去5年，共新增造林绿化面积134万亩．将1 340 000用科学记数法表示为．

查看试题解析
10. 林业部门要考察某种幼树在一定条件下的移植成活率，下图是这种幼树在移植过程中幼树成活率的统计图：
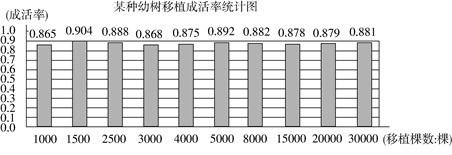
估计该种幼树在此条件下移植成活的概率为（结果精确到0.01）．

查看试题解析
11. 计算： $2 + 2 \overset{m 个 2}{\overset{︷}{+}} \dots + 2 + 3 \times 3 \overset{n 个 3}{\overset{︷}{\times}} \dots \times 3 =$ ．

查看试题解析
12. 如图，测量小玻璃管口径的量具ABC上，AB的长为10毫米，AC被分为60等份，如果小管口中DE正好对着量具上20份处（DE∥AB），那么小管口径DE的长是毫米．

查看试题解析
13. 已知：a²+a=4，则代数式a（2a+1）﹣（a+2）（a﹣2）的值是．

查看试题解析
14. 如图，AB是⊙O的直径，弦CD⊥AB于点E，若AB=10，CD=8，则BE= ．

查看试题解析
15. 如图，在△ABC中，点E，F分别是AC，BC的中点，若S_{四边形ABFE}=9，则S_三角形EFC= ．

查看试题解析
16. ▱ABCD中，对角线AC、BD相交于点O ， E是边AB上的一个动点（不与A、B重合），连接EO并延长，交CD于点F ，连接AF ， CE ，下列四个结论中：
①对于动点E ，四边形AECF始终是平行四边形；

②若∠ABC＜90°，则至少存在一个点E ，使得四边形AECF是矩形；

③若AB＞AD ，则至少存在一个点E ，使得四边形AECF是菱形；

④若∠BAC＝45°，则至少存在一个点E ，使得四边形AECF是正方形．

以上所有正确说法的序号是．

查看试题解析

三、解答题

17. 计算：（ $\frac{1}{3}$ ）^﹣1﹣（π﹣ $\sqrt{3}$ ）⁰+|1﹣ $\sqrt{3}$ |﹣2sin60°．

查看试题解析
18. 解不等式组 ${\begin{array}{l} 3 (x - 1) \geq 4 x - 5 \\ x - 1 > \frac{x - 5}{3} \end{array}$ ，并写出它的所有整数解．

查看试题解析
19. 如图，在 $△ A B C$ 中， $A B = A C$ ，点 $D$ 是 $B C$ 边上一点， $D E ∥ A B$ ．交 $A C$ 于点 $E$ ，连结 $D E$ ，过点 $E$ 作 $E F ⊥ B C$ 于点 $F$ ，求证： $F$ 为线段 $C D$ 中点．

查看试题解析
20. 关于x的一元二次方程 $x^{2} + 2 x + k - 1 = 0$ 有两个不相等的实数根.

(1)、求k的取值范围；

(2)、当k为正整数时，求此时方程的根.

查看试题解析
21. 如图，在平面直角坐标系 $x O y$ 中，函数 $y = \frac{k}{x} (k \neq 0)$ 的图象与直线 $y = x + 1$ 交于点 $A (2 ， a)$ ．

(1)、求 $a$ ， $k$ 的值；

(2)、连结 $O A$ ，点 $P$ 是函数 $y = \frac{k}{x} (k \neq 0)$ 上一点，且满足 $O P = O A$ ，直接写出点 $P$ 的坐标（点 $A$ 除外）．

查看试题解析
22. 如图，已知平行四边形ABCD，延长 $A B$ 到E使 $B E = A B$ ，连接 $B D$ ， $E D$ ， $E C$ ，若 $E D = A D$ ．

(1)、求证：四边形 $B E C D$ 是矩形；

(2)、连接 $A C$ ，若 $A D = 8$ ， $C D = 4$ ，求 $A C$ 的长．

查看试题解析

23. 为了解某区初二年级数学学科期末质量监控情况，进行了抽样调查，过程如下，请将有关问题补充完整．收集数据：随机抽取甲乙两所学校的名学生的数学成绩进行分析：

甲 91 89 77 86 71 31 97 93 72 91 81 92 85 85 95 88 88 90 44 91

乙 84 93 66 69 76 87 77 82 85 88 90 88 67 88 91 96 68 97 59 88

(1)、整理、描述数据：

按如下数据段整理、描述这两组数据，分析数据：

分段

学校

$\begin{array}{l} 30 \leq x \\ \leq 39 \end{array}$

$\begin{array}{l} 40 \leq x \\ \leq 49 \end{array}$

$\begin{array}{l} 50 \leq x \\ \leq 59 \end{array}$

$\begin{array}{l} 60 \leq x \\ \leq 69 \end{array}$

$\begin{array}{l} 70 \leq x \\ \leq 79 \end{array}$

$\begin{array}{l} 80 \leq x \\ \leq 89 \end{array}$

$\begin{array}{l} 90 \leq x \\ \leq 100 \end{array}$

甲

乙

(2)、两组数据的平均数、中位数、众数、方差如下表：

统计量

学校

平均数

中位数

众数

方差

甲

81.85

$m$

268.43

乙

81.95

115.25

经统计，表格中 $m$ 的值是．

(3)、得出结论

①若甲学校有600名初二学生，估计这次考试成绩80分以上人数为．

②可以推断出学校学生的数学水平较高，理由为：．（至少从两个不同的角度说明推断的合理性）

查看试题解析

24. 如图，以 $A B$ 为直径作 $⊙ O$ ，过点 $A$ 作 $⊙ O$ 的切线 $A C$ ，连结 $B C$ ，交 $⊙ O$ 于点 $D$ ，点 $E$ 是 $B C$ 边的中点，连结 $A E$ ．

(1)、求证： $∠ A E B = 2 ∠ C$ ；

(2)、若 $A B = 5$ ， $\tan B = \frac{4}{3}$ ，求 $D E$ 的长．

查看试题解析
25. 在平面直角坐标系 $x O y$ 中，抛物线 $y = a x^{2} + b x - 5 a$ 与 $y$ 轴交于点 $A$ ，将点 $A$ 向左平移4个单位长度，得到点 $B$ ，点 $B$ 在抛物线上．

(1)、求点 $B$ 的坐标（用含a的式子表示）；

(2)、求抛物线的对称轴；

(3)、已知点 $P (- 1 ， - 2 a)$ ， $Q (- 4 ， 2)$ ．若抛物线与线段 $P Q$ 恰有一个公共点，结合函数图象，求 $a$ 的取值范围．

查看试题解析
26. 如图1，在 $△ A B P$ 中， $∠ A B P = 60 °$ ， $90 ° < ∠ A P B < 120 °$ ，过点 $A$ 的直线 $l$ 垂直于线段 $B P$ 所在的直线．设点 $B$ ， $P$ 关于直线 $l$ 的对称点分别为点 $B^{'}$ ， $P^{'}$

(1)、在图1中画出 $△ A B P$ 关于直线 $l$ 对称的三角形 $△ A B^{'} P^{'}$ ．

(2)、若 $∠ B A P = α$ ，求 $∠ A P^{'} B$ 的度数．（用 $α$ 表示）

(3)、若点 $P^{'}$ 关于直线 $A B^{'}$ 的对称点为 $M$ ，连接 $A M$ ， $P M$ ．请写出 $P A$ 、 $P M$ 之间的数量关系和位置关系，并证明你的结论．

查看试题解析
27. 已知图形 $M$ 和图形 $M$ 上的两点 $P$ 、 $Q$ ，如果 $\overset{⌢}{P Q}$ 上的所有点都在图形 $M$ 的内部或边上，则称 $\overset{⌢}{P Q}$ 为图形 $M$ 的内弧．特别的，在 $△ A B C$ 中， $D$ ， $E$ 分别是 $△ A B C$ 两边的中点，如果 $\overset{⌢}{D E}$ 上的所有点都在 $△ A B C$ 的内部或边上，则称 $\overset{⌢}{D E}$ 为 $△ A B C$ 的中内弧．（注： $\overset{⌢}{P Q}$ 是指劣弧或半圆）在平面直角坐标系中，已知点 $A (4 ， 0)$ $B (0 ， n)$ ．设内弧所在圆的圆心为 $P$ ．

(1)、当 $n = 4$ 时，连接 $O A$ 、 $O B$ 并延长．
①请在图1中画出一条 $∠ A O B$ 的内弧 $\overset{⌢}{A B}$ ；

②请直接写出 $∠ A O B$ 的内弧 $\overset{⌢}{A B}$ 长度的最大值．

(2)、连接 $O A$ 、 $O B$ 并延长．
当 $n = \frac{4}{3} \sqrt{3}$ 时，请直接写出 $∠ A O B$ 的所有内弧 $\overset{⌢}{A B}$ ̂所在圆的圆心 $P$ 的纵坐标的取值范围；

(3)、连接 $O A$ 、 $O B$ 并延长．若直线 $x = 6$ 上存在 $∠ A O B$ 的内弧 $\overset{⌢}{A B}$ ̂所在圆的圆心 $P$ ，请求出 $n$ 的取值范围．

(4)、作点 $B$ 关于点 $O$ 的对称点 $C$ ，作点 $B$ 关于点 $A$ 的对称点 $D$ ，连接 $B C$ 、 $B D$ 、 $C D$ ．令 $n > 0$ ，当 $△ B C D$ 的中内弧 $\overset{⌢}{A O}$ 所在的圆的圆心 $P$ 在 $△ B C D$ 的外部时， $△ B C D$ 的所有中内弧 $\overset{⌢}{A O}$ 都存在，请直接写出 $n$ 的取值范围．

查看试题解析