北京朝阳区2020年中考数学一模试卷
试卷更新日期:2021-03-23 类型:中考模拟
一、单选题
-
1. 自2020年1月23日起,我国仅用大概10天就建成了火神山医院,18天建成了雷神山医院,彰显了“中国速度”.雷神山医院和火神山医院总建筑面积约为113800平方米.将113800用科学记数法表示应为( )A、 B、 C、 D、2. 如图是某几何图形的三视图,则这个几何体是( )


 A、圆锥 B、长方体 C、圆柱 D、球3. 实数 在数轴上的对应点的位置如图所示,这四个数中,相反数最大的是( )
A、圆锥 B、长方体 C、圆柱 D、球3. 实数 在数轴上的对应点的位置如图所示,这四个数中,相反数最大的是( ) A、 B、 C、 D、4. 一个不透明的袋中装有8个黄球, 个红球, 个白球,每个球除颜色外都相同.任意摸出一个球,是黄球的概率与不是黄球的概率相同,下列 与 的关系一定正确的是( )A、 B、 C、 D、5. 如果 ,那么代数式 的值为( )A、3 B、 C、 D、6. 如图, 的直径 垂直于弦 ,垂足为 , , ,则 的长为( )
A、 B、 C、 D、4. 一个不透明的袋中装有8个黄球, 个红球, 个白球,每个球除颜色外都相同.任意摸出一个球,是黄球的概率与不是黄球的概率相同,下列 与 的关系一定正确的是( )A、 B、 C、 D、5. 如果 ,那么代数式 的值为( )A、3 B、 C、 D、6. 如图, 的直径 垂直于弦 ,垂足为 , , ,则 的长为( ) A、2.5 B、4 C、5 D、107. 如图,直线 ,点 在直线 上,以点 为圆心,适当长度为半径画弧,分别交直线 , 于 , 两点,以点 为圆心, 长为半径画弧,与前弧交于点 (不与点 重合),连接 , , , ,其中 交 于点 .若 ,则下列结论错误的是( )
A、2.5 B、4 C、5 D、107. 如图,直线 ,点 在直线 上,以点 为圆心,适当长度为半径画弧,分别交直线 , 于 , 两点,以点 为圆心, 长为半径画弧,与前弧交于点 (不与点 重合),连接 , , , ,其中 交 于点 .若 ,则下列结论错误的是( ) A、 B、 C、 D、8. 生活垃圾分类回收是实现垃圾减量化和资源化的重要途径和手段.为了解2019年某市第二季度日均可回收物回收量情况,随机抽取该市2019年第二季度的 天数据,整理后绘制成统计表进行分析.
A、 B、 C、 D、8. 生活垃圾分类回收是实现垃圾减量化和资源化的重要途径和手段.为了解2019年某市第二季度日均可回收物回收量情况,随机抽取该市2019年第二季度的 天数据,整理后绘制成统计表进行分析.日均可回收物回收量(千吨)
合计
频数
1
2
3
频率
0.05
0.10
0.15
1
表中 组的频率 满足 .
下面有四个推断:
①表中 的值为20;②表中 的值可以为7;③这 天的日均可回收物回收量的中位数在 组;④这 天的日均可回收物回收量的平均数不低于3.所有合理推断的序号是( )
A、①② B、①③ C、②③④ D、①③④二、填空题
-
9. 若分式 有意义,则 的取值范围是.10. 分解因式: .11. 如图,在 中,点 , 分别在 , 上,DE∥BC,若 , ,则 .
 12. 如图所示的网格是正方形网格,则 (填“>”、“=”或“<”).
12. 如图所示的网格是正方形网格,则 (填“>”、“=”或“<”).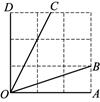 13. 如图, 是六边形 的外角,则 °.
13. 如图, 是六边形 的外角,则 °.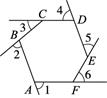 14. 用一个 的值说明命题“若 为实数,则 ”是错误的,这个值可以是 .15. 某地扶贫人员甲从办公室出发,骑车匀速前往所 村走访群众,出发几分钟后,扶贫人员乙发现甲的手机落在办公室,无法联系,于是骑车沿相同的路线匀速去追甲.乙刚出发2分钟,甲也发现自己手机落在办公室,立刻原路原速骑车返回办公室,2分钟后甲遇到乙,乙把手机给甲后立即原路原速返回办公室,甲继续原路原速赶往 村.甲、乙两人相距的路程 (米)与甲出发的时间 (分)之间的关系如图所示(乙给甲手机的时间忽略不计).有下列三个说法:
14. 用一个 的值说明命题“若 为实数,则 ”是错误的,这个值可以是 .15. 某地扶贫人员甲从办公室出发,骑车匀速前往所 村走访群众,出发几分钟后,扶贫人员乙发现甲的手机落在办公室,无法联系,于是骑车沿相同的路线匀速去追甲.乙刚出发2分钟,甲也发现自己手机落在办公室,立刻原路原速骑车返回办公室,2分钟后甲遇到乙,乙把手机给甲后立即原路原速返回办公室,甲继续原路原速赶往 村.甲、乙两人相距的路程 (米)与甲出发的时间 (分)之间的关系如图所示(乙给甲手机的时间忽略不计).有下列三个说法: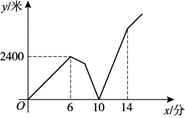
①甲出发10分钟后与乙相遇;
②甲的速度是400米/分;
③乙返回办公室用时4分钟.
其中所有正确说法的序号是 .
16. 某兴趣小组外出登山,乘坐缆车的费用如下表所示:乘坐缆车方式
乘坐缆车费用(单位:元/人)
往返
180
单程
100
已知小组成员每个人都至少乘坐一次缆车,去程时有8人乘坐缆车,返程时有17人乘坐缆车,他们乘坐缆车的总费用是2400元,该小组共有人.
三、解答题
-
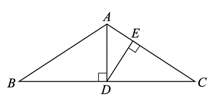
17. 计算: .18. 解不等式组:19. 如图,在 中, , 于点 于点 .
求证: .
 20. 关于x的一元二次方程 有两个不相等的实数根.(1)、求m的取值范围;(2)、写出一个符合条件的 的值,并求出此时方程的根.21. 如图,四边形 是平行四边形, ,垂足分别为 ,且 .
20. 关于x的一元二次方程 有两个不相等的实数根.(1)、求m的取值范围;(2)、写出一个符合条件的 的值,并求出此时方程的根.21. 如图,四边形 是平行四边形, ,垂足分别为 ,且 .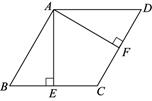 (1)、求证:四边形 是菱形;(2)、连接EF并延长,交AD的延长线于点G,若 ,求EG的长.22. 先进制造业城市发展指数是反映一个城市先进制造水平的综合指数.对2019年我国先进制造业城市发展指数得分排名位居前列的30个城市的有关数据进行收集、整理、描述和分析.下面给出了部分信息:
(1)、求证:四边形 是菱形;(2)、连接EF并延长,交AD的延长线于点G,若 ,求EG的长.22. 先进制造业城市发展指数是反映一个城市先进制造水平的综合指数.对2019年我国先进制造业城市发展指数得分排名位居前列的30个城市的有关数据进行收集、整理、描述和分析.下面给出了部分信息:a . 先进制造业城市发展指数得分的频数分布直方图(数据分成6组: ):
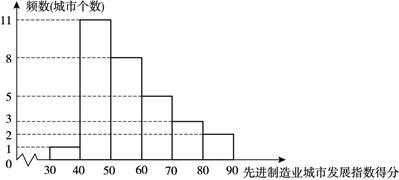
b . 先进制造业城市发展指数得分在 这一组的是:71.1 75.7 79.9
c.30个城市的2019年快递业务量累计和先进制造业城市发展指数得分情况统计图:
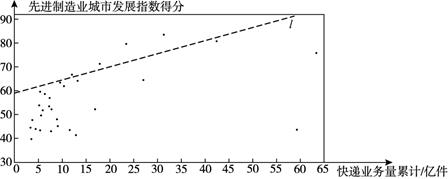
d . 北京的先进制造业城市发展指数得分为79.9.
根据以上信息,回答下列问题:
(1)、在这30个城市中,北京的先进制造业城市发展指数排名第;(2)、在30个城市的快递业务量累计和先进制造业城市发展指数得分情况统计图中,包括北京在内的少数几个城市所对应的点位于虚线 的上方.请在图中用“○”圈出代表北京的点;(3)、在这30个城市中,先进制造业城市发展指数得分高于北京的城市的快递业务量累计的最小值约为亿件.(结果保留整数)23. 如图,在 中, .在同一平面内, 内部一点 到 的距离都等于 ( 为常数),到点 的距离等于 的所有点组成图形 . (1)、直接写出 的值;(2)、连接 并延长,交 于点 ,过点 作 于点 .
(1)、直接写出 的值;(2)、连接 并延长,交 于点 ,过点 作 于点 .①求证: ;
②求直线 与图形 的公共点个数.
24. 有这样一个问题:探究函数 的图象与性质并解决问题.小明根据学习函数的经验,对问题进行了探究.
下面是小明的探究过程,请补充完整:
(1)、函数 的自变量 的取值范围是;(2)、取几组 与 的对应值,填写在下表中.…
-4
-2
-1
0
1
1.2
1.25
2.75
2.8
3
4
5
6
8
…
…
1
1.5
2
3
6
7.5
8
8
7.5
6
3
1.5
1
…
的值为;
(3)、如下图,在平面直角坐标系 中,描出补全后的表中各组对应值所对应的点,并画出该函数的图象; (4)、获得性质,解决问题:
(4)、获得性质,解决问题:①通过观察、分析、证明,可知函数 的图象是轴对称图形,它的对称轴是;
②过点 作直线 轴,与函数 的图象交于点 (点 在点 的左侧),则 的值为 .
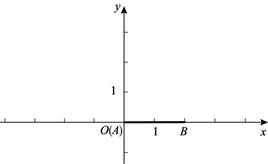
25. 在平面直角坐标系 中,直线 与一次函数 的图象交于点 与反比例函数 的图象交于点 ,点 与点 关于 轴对称.(1)、直接写出点 的坐标;(2)、求点 的坐标(用含m的式子表示);(3)、若 两点中只有一个点在线段 上,直接写出 的取值范围.26. 在平面直角坐标系 中,抛物线 与 轴交于点 .(1)、求点 的坐标(用含 的式子表示);(2)、求抛物线的对称轴;(3)、已知点 .若抛物线与线段 恰有一个公共点,结合函数图象,求 的取值范围.