安徽省宿州市砀山县2020-2021学年八年级上学期数学期末试卷

试卷更新日期：2021-03-23 类型：期末考试

进入出卷网下载

一、选择题(每小题3分，共30分)

1. 下列各数中无理数是（）

A、53131131113 B、 $\sqrt{8}$ C、 $\frac{22}{7}$ D、 ${}^{3}{\sqrt{- 27}}$

查看试题解析
2. 已知点P (a，3+a)在第二象限，则a的取值范围是（）

A、a<0 B、a>-3 C、-3<a<0 D、a<- 3

查看试题解析
3. 如果a是2021的算术平方根，则 $\frac{2021}{100}$ 的算术平方根是（）

A、 $\frac{a}{10}$ B、 $\frac{a}{100}$ C、± $\frac{a}{100}$ D、 $\frac{a^{2}}{10}$

查看试题解析
4. 一次函数y=2x+m的图象上有两点A(x₁ ， $\frac{3}{2}$ ) 、B(x₂ ， 5)，则x₁与x₂的大小关系是（）

A、x₁<x₂ B、x₁>x₂ C、x₁=x₂ D、无法确定

查看试题解析
5. 下列命题中是真命题的是（）

A、中位数就是一组数据中最中间的一个数 B、这组数据0，2，3，3，4，6的方差是2.1 C、一组数据的标准差越大，这组数据就越稳定 D、如果x₁ ， x₂ ， x₃…x_n的平均数是x，那么(x₁- $\bar{x}$ ) + (x₂- $\bar{x}$ )…+ (x_n- $\bar{x}$ ) =0

查看试题解析
6. 一次演讲比赛中，评委将从演讲内容、演讲能力、演讲效果三方面为选手打分，并分别按 $5 : 3 : 2$ 的比例计入总评成绩，小明的三项成绩分别是 $90$ ， $95$ ， $90$ （单位：分）他的总评成绩是（）

A、 $91$ 分 B、 $91.5$ 分 C、 $92$ 分 D、 $92.5$ 分

查看试题解析
7. 一副三角板按如图方式摆放，且∠1的度数比∠2的度数大50°，若设∠1=x°，∠2=y°，则可得到方程组为（）

A、 ${\begin{cases} x = y - 50 \\ x + y = 180 \end{cases}$ B、 ${\begin{cases} x = y + 50 \\ x + y = 180 \end{cases}$ C、 ${\begin{cases} x = y + 50 \\ x + y = 90 \end{cases}$ D、 ${\begin{cases} x = y - 50 \\ x + y = 90 \end{cases}$

查看试题解析
8. 如图，直线AB、CD被BC所截，若AB∥CD，∠1=50°，∠2=40°，则<3的（）

A、80° B、70° C、90° D、100°

查看试题解析
9. 如图，一次函数y=kx+b与y=x+2的图象相交于点P(m，4)，则方程组 ${\begin{cases} y = x + 2 \\ y = k x + b \end{cases}$ 的解是（）

A、(2，4) B、(-2，4) C、(4，2) D、(4，-2)

查看试题解析
10. 甲、乙两人在笔直的公路上同起点、同终点、同方向匀速步行2400米，先到终点的人原地休息。已知甲先出发4分钟，在整个步行过程中，甲、乙两人的距离y(米)与甲出发的时向t(分)之间的函数关系如图所示；下列说法中正确的是（）

A、甲步行的速度为8米/分 B、乙走完全程用了34分钟 C、乙用16分钟追上甲 D、乙到达终点时，甲离终点还有360米

查看试题解析

二、填空题(每小题4分，共32分)

11. 当x时，二次根式 $\sqrt{x}$ -3在实数范围内有意义。

查看试题解析
12. 已知一次函数y=-3x+1-m²经过原点，则m=。

查看试题解析
13. 点P关于X轴的对称点为(2，-3)，则P点坐标为。

查看试题解析
14. 最简二次根式 $\sqrt{b + 2}$ 与 ${}^{a - 1}{\sqrt{5 - 2 b}}$ 是同类最简二次根式，则a-b=。

查看试题解析
15. 已知二元一次方程组 ${\begin{cases} 2 m - n = 3 \\ m - 2 n = 4 \end{cases}$ ，则m-n的值是。

查看试题解析
16. 已知某直线经过点A(0，1)，且与两坐标轴围成的三角形的面积为2；则该直线的函数表达式是。

查看试题解析
17. 如图， $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $B C = 3$ ， $A C = 4$ ．以 $A B$ 为边在点 $C$ 同侧作正方形 $A B D E$ ，则图中阴影部分的面积为．

查看试题解析
18. 在一单位为1的方格纸上，有一列点A₁ ， A₂ ， A₃ ， …A_n…，(其中n为正整数)均为网格上的格点，按如图所示规律排列，点A₁(2，0)，A₂(1，-1)，A₃(0，0)，A₄(2，2) …则A₂₀₂₁的坐标为。

查看试题解析

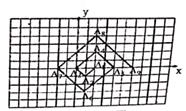
三、解答题(共58分)

19. 计算：

(1)、 $\sqrt{18} + \sqrt{\frac{1}{3}} \times \sqrt{24} + (\sqrt{2} + 1) (\sqrt{2} - 1)$

(2)、解下列方程： ${\begin{cases} 2 x + y = 5 \\ x - 2 y = 0 \end{cases}$

查看试题解析
20. 如图，在离水面高度为5米的岸上，有人用绳子拉船靠岸，开始时绳子BC的长为13米，此人以0.5米每秒的速度收绳，6秒后船移动到点D的位置，问船向岸边移动了多少米？(假设绳子是直的，结果精确到0.1米， $\sqrt{2}$ =1.414， $\sqrt{3}$ =1.732)

查看试题解析
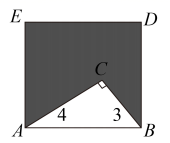
21. 如图，点B在AC上，AF与BD、CE分别交于H、G，已知∠1=50°，∠2=130°，∠ABD=∠A。

(1)、证明：∠C=∠A；

(2)、求∠C的度数。

查看试题解析
22. 一家蔬菜公司收购到某种绿色蔬菜140吨，进行加工后销售：粗加工后销售每吨可获利1000元，精加工后销售每吨获利2000元：已知该公司的加工能力是：每天能精加工5吨或粗加工15吨，但两种加工不能同时进行．受季节等条件的限制，公司必须在-．定时间内将这批蔬菜全部加工后销售完。

(1)、如果要求12天刚好加工完140吨蔬菜，则公司应安排几天精加工，几天粗加工？

(2)、如果先进行精加工，然后进行粗加工。
①试求出销售利润W元与精加工的蔬菜吨数m之间的函数关系式；

②若要求在不超过10天的时间内，将140吨蔬菜全部加工完后进行销售，则加工这批蔬菜最多获得多少利润？此时如何分配加工时间？

查看试题解析
23. 已知点A(4，0)及在第一象限的动点P(x，y)，且x+y=6，设△OPA的面积为S。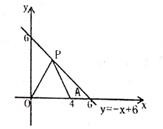

(1)、用含x的式子表示S，并写出自变量x的取值范围；

(2)、求S=9时P点坐标；

(3)、在(2)的基础上，设点Q为y轴上一动点，当PQ+AQ的值最小时，求点Q坐标。

查看试题解析