初中数学湘教版九年级下册第三章 投影与视图 章末检测(提高练)
试卷更新日期:2021-03-22 类型:单元试卷
一、单选题
-
1. 下图中各图形经过折叠后可以围成一个棱柱的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列说法中,符合题意的个数是( )
2. 下列说法中,符合题意的个数是( )①柱体的两个底面一样大;②圆柱、圆锥的底面都是圆;③棱柱的底面是四边形;④长方体一定是柱体;⑤棱柱的侧面一定是长方形.
A、2个 B、3个 C、4个 D、5个3. 如图所示,一电线杆AB的影子分别落在了地上和墙上,某一时刻,小明竖起1米高的直杆,量得其影长为0.5米,此时,他又量得电线杆AB落在地上的影子BD长3米,落在墙上的影子CD的高为2米,小明用这些数据很快算出了电线杆AB的高,请你计算,电线杆AB的高为( ) A、5米 B、6米 C、8米 D、10米4. 学校教学楼前面有一根高是4.2米的旗杆,在某时刻太阳光下的影子长是6.3米,与此同时, 在旗杆周边的一棵大树在地面上投影出的影子长是9米,则此大树的高度是( )A、4.8米 B、8.4米 C、6米 D、9米5. 圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面圆环形阴影的面积是( )
A、5米 B、6米 C、8米 D、10米4. 学校教学楼前面有一根高是4.2米的旗杆,在某时刻太阳光下的影子长是6.3米,与此同时, 在旗杆周边的一棵大树在地面上投影出的影子长是9米,则此大树的高度是( )A、4.8米 B、8.4米 C、6米 D、9米5. 圆桌面(桌面中间有一个直径为0.4m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为1.2m,桌面离地面1m,若灯泡离地面3m,则地面圆环形阴影的面积是( ) A、0.324πm2 B、0.288πm2 C、1.08πm2 D、0.72πm26.
A、0.324πm2 B、0.288πm2 C、1.08πm2 D、0.72πm26.如图,小红居住的小区内有一条笔直的小路,小路的正中间有一路灯,晚上小红由A处径直走到B处,她在灯光照射下的影长l与行走的路程S之间的变化关系用图象刻画出来,大致图象是( )
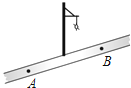 A、
A、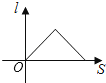
B、
B、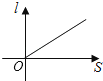
C、
C、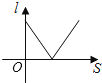
D、
D、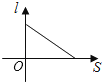 7. 如图,从一块直径是8m的圆形铁皮上剪出一个圆心角为90°的扇形,将剪下的扇形围成一个圆锥,圆锥的高是( )m.
7. 如图,从一块直径是8m的圆形铁皮上剪出一个圆心角为90°的扇形,将剪下的扇形围成一个圆锥,圆锥的高是( )m.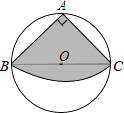 A、4 B、5 C、 D、28. 一个直棱柱,主视图是边长为2 的正方形,俯视图是边长为2 的正三角形,则左视图的面积为 ( )A、12 B、12 C、6 D、39. 若干个相同的正方体组成一个几何体,从不同方向看可以得到如图所示的形状,则这个几何体最多可由多少个这样的正方体组成?( )
A、4 B、5 C、 D、28. 一个直棱柱,主视图是边长为2 的正方形,俯视图是边长为2 的正三角形,则左视图的面积为 ( )A、12 B、12 C、6 D、39. 若干个相同的正方体组成一个几何体,从不同方向看可以得到如图所示的形状,则这个几何体最多可由多少个这样的正方体组成?( )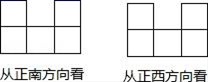 A、12个 B、13个 C、14个 D、18个10. 某三棱锥的三视图如图所示,该三棱锥的体积是( )
A、12个 B、13个 C、14个 D、18个10. 某三棱锥的三视图如图所示,该三棱锥的体积是( )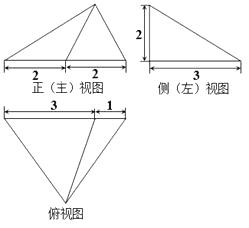 A、 B、4 C、2 D、11. 正如我们小学学过的圆锥体积公式V= πr2h(π表示圆周率,r表示圆锥的底面半径,h表示圆锥的高)一样,许多几何量的计算都要用到π.祖冲之是世界上第一个把π计算到小数点后7位的中国古代科学家,创造了当时世界上的最高水平,差不多过了1000年,才有人把π计算得更精确.在辉煌成就的背后,我们来看看祖冲之付出了多少.现在的研究表明,仅仅就计算来讲,他至少要对9位数字反复进行130次以上的各种运算,包括开方在内.即使今天我们用纸笔来算,也绝不是一件轻松的事情,何况那时候没有现在的纸笔,数学计算不是用现在的阿拉伯数字,而是用算筹(小竹棍或小竹片)进行的,这需要怎样的细心和毅力啊!他这种严谨治学的态度,不怕复杂计算的毅力,值得我们学习.
A、 B、4 C、2 D、11. 正如我们小学学过的圆锥体积公式V= πr2h(π表示圆周率,r表示圆锥的底面半径,h表示圆锥的高)一样,许多几何量的计算都要用到π.祖冲之是世界上第一个把π计算到小数点后7位的中国古代科学家,创造了当时世界上的最高水平,差不多过了1000年,才有人把π计算得更精确.在辉煌成就的背后,我们来看看祖冲之付出了多少.现在的研究表明,仅仅就计算来讲,他至少要对9位数字反复进行130次以上的各种运算,包括开方在内.即使今天我们用纸笔来算,也绝不是一件轻松的事情,何况那时候没有现在的纸笔,数学计算不是用现在的阿拉伯数字,而是用算筹(小竹棍或小竹片)进行的,这需要怎样的细心和毅力啊!他这种严谨治学的态度,不怕复杂计算的毅力,值得我们学习.下面我们就来通过计算解决问题:已知圆锥的侧面展开图是个半圆,若该圆锥的体积等于9 π,则这个圆锥的高等于( )
A、 B、 C、 D、12. 如图,在四边形ABCD中,AB∥CD,∠A=90°,AB=5,CD=2.以A为圆心,AD为半径的圆与BC边相切于点M,与AB交于点E,将扇形A﹣DME剪下围成一个圆锥,则圆锥的高为( ) A、1 B、4 C、 D、
A、1 B、4 C、 D、二、填空题
-
13. 如果一个棱柱是由 个面围成的,那么这个棱柱是棱柱.14. 如图,小军、小珠之间的距离为2.7m,他们在同一盏路灯下的影长分别为1.8m,1.5m,已知小军、小珠的身高分别为1.8m,1.5m,则路灯的高为m.
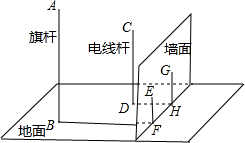
 15. 如图,在一面与地面垂直的围墙的同侧有一根高13米的旗杆AB和一根高度未知的电线杆CD,它们都与地面垂直,为了侧得电线杆的高度,数学兴趣小组的同学进行了如下测量
15. 如图,在一面与地面垂直的围墙的同侧有一根高13米的旗杆AB和一根高度未知的电线杆CD,它们都与地面垂直,为了侧得电线杆的高度,数学兴趣小组的同学进行了如下测量 某一时刻,在太阳光照射下,旗杆落在围墙上的影子EF的长度为3米,落在地面上的影子BF的长为8米,而电信杆落在围墙上的影子GH的长度为 米,落在地面上的银子DH的长为6米,依据这些数据,该小组的同学计算出了电线杆的高度是米
某一时刻,在太阳光照射下,旗杆落在围墙上的影子EF的长度为3米,落在地面上的影子BF的长为8米,而电信杆落在围墙上的影子GH的长度为 米,落在地面上的银子DH的长为6米,依据这些数据,该小组的同学计算出了电线杆的高度是米 
 16. 如图,圆锥的母线长OA为8,底面圆的半径为4.若一只蚂蚁在底面上点A处,在相对母线OC的中点B处有一只小虫,蚂蚁要捉小虫,需要爬行的最短路程为.
16. 如图,圆锥的母线长OA为8,底面圆的半径为4.若一只蚂蚁在底面上点A处,在相对母线OC的中点B处有一只小虫,蚂蚁要捉小虫,需要爬行的最短路程为. 17. 一个几何体的三视图如图所示,则该几何体的表面积为.(π取3)
17. 一个几何体的三视图如图所示,则该几何体的表面积为.(π取3)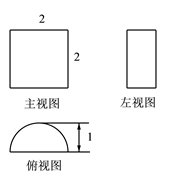 18. 如图是由一些棱长为1的小立方块所搭几何体的三种视图.若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个长方体,至少还需要个小立方块.最终搭成的长方体的表面积是 .
18. 如图是由一些棱长为1的小立方块所搭几何体的三种视图.若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个长方体,至少还需要个小立方块.最终搭成的长方体的表面积是 .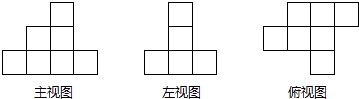
三、解答题
-
19. 小明打算用一张半圆形的纸(如图)做一个圆锥.在制作过程中,他先将半圆剪成面积比为1∶2的两个扇形.
 (1)、请你在图中画出他的裁剪痕迹(要求尺规作图,不写作法,保留作图痕迹);(2)、若半圆半径是3,小明用裁出的大扇形作为圆锥的侧面,请你求出小明所做的圆锥的高.20. 小明用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
(1)、请你在图中画出他的裁剪痕迹(要求尺规作图,不写作法,保留作图痕迹);(2)、若半圆半径是3,小明用裁出的大扇形作为圆锥的侧面,请你求出小明所做的圆锥的高.20. 小明用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题: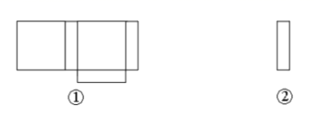 (1)、小明总共剪开了条棱.(2)、现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,请你帮助小明在①上补全.(作图要求:先用尺和铅笔画图,再用黑色的签字笔描一遍)(3)、小明说:已知这个长方形纸盒高为3cm,底面是一个正方形,并且这个长方形纸盒所有棱长的和是92cm,请计算,这个长方体纸盒的体积是cm3 .21. 如图,是某几何体从三个方向分别看到的图形.
(1)、小明总共剪开了条棱.(2)、现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,请你帮助小明在①上补全.(作图要求:先用尺和铅笔画图,再用黑色的签字笔描一遍)(3)、小明说:已知这个长方形纸盒高为3cm,底面是一个正方形,并且这个长方形纸盒所有棱长的和是92cm,请计算,这个长方体纸盒的体积是cm3 .21. 如图,是某几何体从三个方向分别看到的图形. (1)、说出这个几何体的名称;(2)、若其看到的三个图形中图1的长为 ,宽为 ;图2的宽为 ;图3直角三角形的斜边长为 ,试求这个几何体的所有棱长的和是多少?它的表面积多大?22. 如图,在单位长度为1的正方形网格中建立一直角坐标系,一条圆弧经过网格点A、B、C,完成下列问题:
(1)、说出这个几何体的名称;(2)、若其看到的三个图形中图1的长为 ,宽为 ;图2的宽为 ;图3直角三角形的斜边长为 ,试求这个几何体的所有棱长的和是多少?它的表面积多大?22. 如图,在单位长度为1的正方形网格中建立一直角坐标系,一条圆弧经过网格点A、B、C,完成下列问题: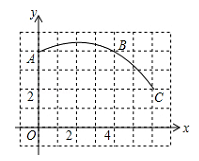 (1)、在图中标出圆心D,则圆心D点的坐标为;(2)、连接AD、CD,则∠ADC的度数为;(3)、若扇形DAC是一个圆锥的侧面展开图,求该圆锥底面半径.23.
(1)、在图中标出圆心D,则圆心D点的坐标为;(2)、连接AD、CD,则∠ADC的度数为;(3)、若扇形DAC是一个圆锥的侧面展开图,求该圆锥底面半径.23.一组合体的三视图如图所示,该组合体是由哪几个几何体组成,并求出该组合体的表面积(单位:cm2).
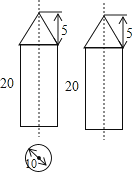 24. 如图,是由一些棱长都为1cm的小正方体组合成的简单几何体.
24. 如图,是由一些棱长都为1cm的小正方体组合成的简单几何体.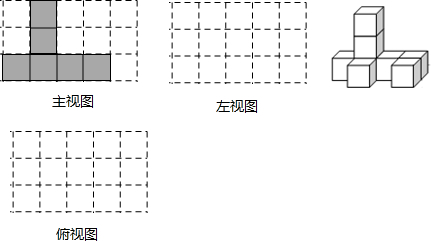 (1)、该几何体的表面积(含下底面)是cm2;(2)、该几何体的主视图如图所示,请在下面方格纸中分别画出它的左视图和俯视图.(3)、若使该几何体主视图、俯视图不发生改变,最多还可以在几何体上再堆放个相同的小正方体.25. 实验学校某班开展数学“综合与实践”测量活动.有两座垂直于水平地面且高度不一的圆柱,两座圆柱后面有一斜坡,且圆柱底部到坡脚水平线 的距离皆为 .王诗嬑观测到高度 矮圆柱的影子落在地面上,其长为 ;而高圆柱的部分影子落在坡上,如图所示.已知落在地面上的影子皆与坡脚水平线 互相垂直,并视太阳光为平行光,测得斜坡坡度 ,在不计圆柱厚度与影子宽度的情况下,请解答下列问题:
(1)、该几何体的表面积(含下底面)是cm2;(2)、该几何体的主视图如图所示,请在下面方格纸中分别画出它的左视图和俯视图.(3)、若使该几何体主视图、俯视图不发生改变,最多还可以在几何体上再堆放个相同的小正方体.25. 实验学校某班开展数学“综合与实践”测量活动.有两座垂直于水平地面且高度不一的圆柱,两座圆柱后面有一斜坡,且圆柱底部到坡脚水平线 的距离皆为 .王诗嬑观测到高度 矮圆柱的影子落在地面上,其长为 ;而高圆柱的部分影子落在坡上,如图所示.已知落在地面上的影子皆与坡脚水平线 互相垂直,并视太阳光为平行光,测得斜坡坡度 ,在不计圆柱厚度与影子宽度的情况下,请解答下列问题: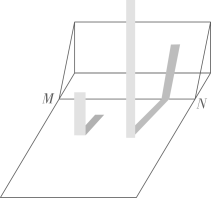
 (1)、若王诗嬑的身高为 ,且此刻她的影子完全落在地面上,则影子长为多少 ?(2)、猜想:此刻高圆柱和它的影子与斜坡的某个横截面一定同在一个垂直于地面的平面内.请直接回答这个猜想是否符合题意?(3)、若同一时间量得高圆柱落在坡面上的影子长为 ,则高圆柱的高度为多少 ?26. 阅读以下文字并解答问题:在“物体的高度”活动中,某数学兴趣小组的4名同学选择了测量学校里的四棵树的高度.在同一时刻的阳光下,他们分别做了以下工作:
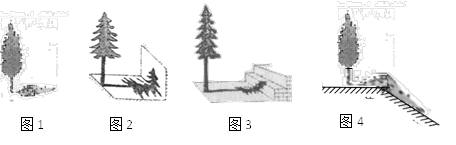
(1)、若王诗嬑的身高为 ,且此刻她的影子完全落在地面上,则影子长为多少 ?(2)、猜想:此刻高圆柱和它的影子与斜坡的某个横截面一定同在一个垂直于地面的平面内.请直接回答这个猜想是否符合题意?(3)、若同一时间量得高圆柱落在坡面上的影子长为 ,则高圆柱的高度为多少 ?26. 阅读以下文字并解答问题:在“物体的高度”活动中,某数学兴趣小组的4名同学选择了测量学校里的四棵树的高度.在同一时刻的阳光下,他们分别做了以下工作:小芳:测得一根长为1米的竹竿的影长为0.8米,甲树的影长为4.08米(如图1).
小华:发现乙树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图2),墙壁上的影长为1.2米,落在地面上的影长为2.4米.
小丽:测量的丙树的影子除落在地面上外,还有一部分落在教学楼的第一级台阶上(如图3),测得此影子长为0.2米,一级台阶高为0.3米,落在地面上的影长为4.4米.
小明:测得丁树落在地面上的影长为2.4米,落在坡面上影长为3.2米(如图4).身高是1.6m的小明站在坡面上,影子也都落坡面上,小芳测得他的影长为2m.
 (1)、在横线上直接填写甲树的高度为米.(2)、求出乙树的高度(画出示意图).(3)、请选择丙树的高度为( )A、6.5米 B、5.75米 C、6.05米 D、7.25米(4)、你能计算出丁树的高度吗?试试看.
(1)、在横线上直接填写甲树的高度为米.(2)、求出乙树的高度(画出示意图).(3)、请选择丙树的高度为( )A、6.5米 B、5.75米 C、6.05米 D、7.25米(4)、你能计算出丁树的高度吗?试试看.