2016年浙江省温州市中考数学试卷

试卷更新日期：2016-07-22 类型：中考真卷

进入出卷网下载

一、（共10小题，每小题4分，满分40分，在每小题给出的四个选项中，只有一个是符合题意的，请把正确的选项填在题后的括号内）

1. 计算（+5）+（﹣2）的结果是（）

A、7 B、﹣7 C、3 D、﹣3

查看试题解析
2.
如图是九（1）班45名同学每周课外阅读时间的频数直方图（每组含前一个边界值，不含后一个边界值）．由图可知，人数最多的一组是（）

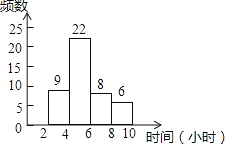A、2～4小时 B、4～6小时 C、6～8小时 D、8～10小时

查看试题解析
3.
三本相同的书本叠成如图所示的几何体，它的主视图是（）

A、 B、 C、 D、

查看试题解析
4. 已知甲、乙两数的和是7，甲数是乙数的2倍．设甲数为x，乙数为y，根据题意，列方程组正确的是（）

A、 ${\begin{cases} x + y = 7 \\ x = 2 y \end{cases}$ B、 ${\begin{cases} x + y = 7 \\ y = 2 x \end{cases}$ C、 ${\begin{cases} x + 2 y = 7 \\ x = 2 y \end{cases}$ D、 ${\begin{cases} 2 x + y = 7 \\ y = 2 x \end{cases}$

查看试题解析
5. 若分式 $\frac{x - 2}{x + 3}$ 的值为0，则x的值是（）

A、﹣3 B、﹣2 C、3 D、2

查看试题解析
6. 一个不透明的袋中，装有2个黄球、3个红球和5个白球，它们除颜色外都相同．从袋中任意摸出一个球，是白球的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{3}{10}$ D、 $\frac{1}{5}$

查看试题解析
7. 六边形的内角和是（）

A、540° B、720° C、900° D、1080°

查看试题解析
8.
如图，一直线与两坐标轴的正半轴分别交于A，B两点，P是线段AB上任意一点（不包括端点），过P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为10，则该直线的函数表达式是（）

A、y=x+5 B、y=x+10 C、y=﹣x+5 D、y=﹣x+10

查看试题解析
9.
如图，一张三角形纸片ABC，其中∠C=90°，AC=4，BC=3．现小林将纸片做三次折叠：第一次使点A落在C处；将纸片展平做第二次折叠，使点B落在C处；再将纸片展平做第三次折叠，使点A落在B处．这三次折叠的折痕长依次记为a，b，c，则a，b，c的大小关系是（）

A、c＞a＞b B、b＞a＞c C、c＞b＞a D、b＞c＞a

查看试题解析
10.
如图，在△ABC中，∠ACB=90°，AC=4，BC=2．P是AB边上一动点，PD⊥AC于点D，点E在P的右侧，且PE=1，连结CE．P从点A出发，沿AB方向运动，当E到达点B时，P停止运动．在整个运动过程中，图中阴影部分面积S₁+S₂的大小变化情况是（）

A、一直减小 B、一直不变 C、先减小后增大 D、先增大后减小

查看试题解析

二、填空题（共6小题，每小题5分，满分30分）

11. 因式分解：a²﹣3a=

查看试题解析
12. 某小组6名同学的体育成绩（满分40分）分别为：36，40，38，38，32，35，这组数据的中位数是分．

查看试题解析
13. 方程组 ${\begin{cases} x + 2 y = 5 \\ 3 x - 2 y = 7 \end{cases}$ 的解是

查看试题解析
14.
如图，将△ABC绕点C按顺时针方向旋转至△A′B′C，使点A′落在BC的延长线上．已知∠A=27°，∠B=40°，则∠ACB′=度．

查看试题解析
15.
七巧板是我们祖先的一项卓越创造，被誉为“东方魔板”，小明利用七巧板（如图1所示）中各板块的边长之间的关系拼成一个凸六边形（如图2所示），则该凸六边形的周长是cm．

查看试题解析
16.
如图，点A，B在反比例函数y= $\frac{k}{x}$ （k＞0）的图象上，AC⊥x轴，BD⊥x轴，垂足C，D分别在x轴的正、负半轴上，CD=k，已知AB=2AC，E是AB的中点，且△BCE的面积是△ADE的面积的2倍，则k的值是

查看试题解析

三、解答题（共8小题，满分80分）

17. 计算：

(1)、 $\sqrt{20}$ +（﹣3）²﹣（ $\sqrt{2}$ ﹣1）⁰

(2)、化简：（2+m）（2﹣m）+m（m﹣1）．

查看试题解析
18.
为了解学生对“垃圾分类”知识的了解程度，某学校对本校学生进行抽样调查，并绘制统计图，其中统计图中没有标注相应人数的百分比．请根据统计图回答下列问题：

(1)、求“非常了解”的人数的百分比．

(2)、已知该校共有1200名学生，请估计对“垃圾分类”知识达到“非常了解”和“比较了解”程度的学生共有多少人？

查看试题解析
19.
如图，E是▱ABCD的边CD的中点，延长AE交BC的延长线于点F．

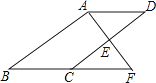(1)、求证：△ADE≌△FCE．

(2)、若∠BAF=90°，BC=5，EF=3，求CD的长．

查看试题解析
20.
如图，在方格纸中，点A，B，P都在格点上．请按要求画出以AB为边的格点四边形，使P在四边形内部（不包括边界上），且P到四边形的两个顶点的距离相等．

(1)、在图甲中画出一个▱ABCD．

(2)、在图乙中画出一个四边形ABCD，使∠D=90°，且∠A≠90°．（注：图甲、乙在答题纸上）

查看试题解析
21.
如图，在△ABC中，∠C=90°，D是BC边上一点，以DB为直径的⊙O经过AB的中点E，交AD的延长线于点F，连结EF．

(1)、求证：∠1=∠F．

(2)、若sinB= $\frac{\sqrt{5}}{5}$ ，EF=2 $\sqrt{5}$ ，求CD的长．

查看试题解析
22. 有甲、乙、丙三种糖果混合而成的什锦糖100千克，其中各种糖果的单价和千克数如表所示，商家用加权平均数来确定什锦糖的单价．

甲种糖果
乙种糖果
丙种糖果
单价（元/千克）
15
25
30
千克数
40
40
20

(1)、求该什锦糖的单价．

(2)、为了使什锦糖的单价每千克至少降低2元，商家计划在什锦糖中加入甲、丙两种糖果共100千克，问其中最多可加入丙种糖果多少千克？

查看试题解析
23.
如图，抛物线y=x²﹣mx﹣3（m＞0）交y轴于点C，CA⊥y轴，交抛物线于点A，点B在抛物线上，且在第一象限内，BE⊥y轴，交y轴于点E，交AO的延长线于点D，BE=2AC．

(1)、用含m的代数式表示BE的长．

(2)、当m= $\sqrt{3}$ 时，判断点D是否落在抛物线上，并说明理由．

(3)、若AG∥y轴，交OB于点F，交BD于点G．
①若△DOE与△BGF的面积相等，求m的值．
②连结AE，交OB于点M，若△AMF与△BGF的面积相等，则m的值是．

查看试题解析
24.
如图，在射线BA，BC，AD，CD围成的菱形ABCD中，∠ABC=60°，AB=6 $\sqrt{3}$ ，O是射线BD上一点，⊙O与BA，BC都相切，与BO的延长线交于点M．过M作EF⊥BD交线段BA（或射线AD）于点E，交线段BC（或射线CD）于点F．以EF为边作矩形EFGH，点G，H分别在围成菱形的另外两条射线上．

(1)、求证：BO=2OM．

(2)、设EF＞HE，当矩形EFGH的面积为24 $\sqrt{3}$ 时，求⊙O的半径．

(3)、当HE或HG与⊙O相切时，求出所有满足条件的BO的长．

查看试题解析

	甲种糖果	乙种糖果	丙种糖果
单价（元/千克）	15	25	30
千克数	40	40	20