浙江省宁波市奉化区2020-2021学年七年级上学期数学期末考试试卷

试卷更新日期：2021-03-22 类型：期末考试

进入出卷网下载

一、单选题

1. 宁波至奉化城际铁路于2020年9月27日上午 $10 : 00$ 正式开通运营，该线路自鄞州区高塘桥站向南引出止于奉化区金海路站，全长21530米，为奉化居民往返宁波城区的交通出行提供极大便利，其中21530用科学记数法表示为（）

A、 $2.153 \times 10^{4}$ B、 $21.53 \times 10^{3}$ C、 $0.2153 \times 10^{5}$ D、 $2.153 \times 10^{3}$

查看试题解析
2. 在0，2， $- \frac{1}{3}$ ，-2四个数中，最小的数是（）

A、0 B、2 C、 $- \frac{1}{3}$ D、-2

查看试题解析
3. 随着校园足球的推广，越来越多的青少年喜爱足球这项运动．下图检测了4个足球的质量，其中超过标准质量的克数记为正数，不足标准质量的克数记为负数，从符合标准质量的角度看，最接近标准的是（）

A、 B、 C、 D、

查看试题解析
4. 下列计算正确的是（）

A、 $3 (a + b) = 3 a + b$ B、 $- a^{2} b + b a^{2} = 0$ C、 $x^{2} + 2 x^{2} = 3 x^{4}$ D、 $2 m + 3 n = 5 m n$

查看试题解析
5. 已知 $x = 1$ 是关于x的一元一次方程 $2 x - a = 0$ 的解，则a的值为（）

A、-1 B、-2 C、1 D、2

查看试题解析
6. 多项式 $2 x^{5} + 4 x y^{3} - 5 x^{2} - 1$ 的次数和常数项分别是（）

A、5，-1 B、5，1 C、10，-1 D、11，-1

查看试题解析
7. 如图，点D把线段AB从左至右依次分成1∶2两部分，点C是AB的中点，若 $D C = 3$ ，则线段AB的长是（）

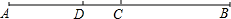A、18 B、12 C、16 D、14

查看试题解析
8. 新型冠状肺炎疫情正在全球蔓延肆虐，口罩成了人们生活中必不可少的物品，某口罩厂有26名工人，每人每天可以生产800个口罩面或1000个口罩耳绳，一个口罩面需要配两个耳绳，为使每天生产的口罩刚好配套，设安排x名工人生产口罩面，则下面所列方程正确的是（）

A、 $2 \times 1000 (26 - x) = 800 x$ B、 $1000 (13 - x) = 800 x$ C、 $1000 (26 - x) = 2 \times 800 x$ D、 $1000 (26 - x) = 800 x$

查看试题解析
9. 计算： $3^{1} - 1 = 2$ ， $3^{2} - 1 = 8$ ， $3^{3} - 1 = 26$ ， $3^{4} - 1 = 80$ ， $3^{5} - 1 = 242$ ，……，归纳各计算结果中的个位数字的规律，猜测 $3^{2021}$ 的个位数字是（）

A、0 B、1 C、2 D、3

查看试题解析
10. 已知长方形ABCD ， $A D > A B$ ， $A D = 10$ ，将两张边长分别为a和b（ $a > b$ ）的正方形纸片按图1，图2两种方式放置（图1，图2中两张正方形纸片均有部分重叠），矩形中未被这两张正方形纸片覆盖的部分用阴影表示，设图1中阴影部分的面积为 $S_{1}$ ，图2中阴影部分的面积为 $S_{2}$ ．当 $S_{2} - S_{1} = 3 b$ 时，AB的值是（）

A、7 B、8 C、9 D、10

查看试题解析

二、填空题

11. 2020的倒数是。

查看试题解析
12. 已知 $∠ α = 20 ° 2 0^{'}$ ，则 $∠ α$ 的余角为．

查看试题解析
13. 如果 $\sqrt{a + 2} + | b - 3 | = 0$ ，那么 $a^{b} =$ ．

查看试题解析
14. 已知等式：① $\frac{x}{3} = \frac{y}{5}$ ② $2 x = 5 y - x$ ③ $3 x - 5 y = 0$ ④ $\frac{x - y}{y} = \frac{2}{3}$ ，其中可以通过适当变形得到 $3 x = 5 y$ 的等式是．（填序号）

查看试题解析
15. 已知代数式 $3 x^{2} - 4 x + 6$ 的值为 $- 8$ ，那么 $- \frac{3}{2} x^{2} + 2 x - 4$ 的值为．

查看试题解析
16. 如图，已知一周长为 30cm 的圆形轨道上有相距 10cm 的 A、B 两点 (备注：圆形轨道上两点的距离是指圆上这两点间较短部分展直后的线段长)．动点P从A点出发，以 7 cm/s 的速度在轨道上按逆时针方向运动，与此同时，动点 Q 从 B 出发，以 3 cm/s 的速度按同样的方向运动．设运动时间为 t (s)，在 P、Q第二次相遇前，当动点 P、Q在轨道上相距 12cm 时，则 t=s．

查看试题解析

三、解答题

17. 计算：

(1)、 $(\frac{7}{9} - \frac{5}{6} + \frac{3}{4}) \times (- 36)$

(2)、 $- 1^{4} - \frac{1}{6} \times [2 - {(- 3)}^{2}]$

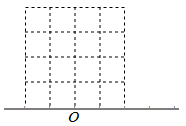
查看试题解析
18. 解下列方程：

(1)、 $5 + 3 x = 2 (5 - x)$

(2)、 $\frac{2 x - 5}{3} = 1 - \frac{2 x + 3}{6}$

查看试题解析
19. 如图是一个 $4 \times 4$ 的正方形网格，每个小正方形的边长都是1，每个小正方形的顶点叫做格点．请你完成：

(1)、画一个面积为8的格点正方形（四个顶点都在方格的顶点上）；

(2)、将图中的数轴补充完整，并用圆规在数轴上表示实数 $\sqrt{8}$ ．

查看试题解析
20. 已知 $X = 4 a^{2} + 3 a b, Y = 2 a^{2} - a b + 2 b^{2}$ ．

(1)、化简 $X - 3 Y$

(2)、当 $a = 2$ ， $b = - 1$ 时，求 $X - 3 Y$ 的值．

查看试题解析
21. 数轴上有 $A ， B ， C$ 三点．点 $A ， B$ 表示的数互为相反数，且点 $A$ 在点 $B$ 的左边，同时点 $A ， B$ 相距8个单位；点 $A ， C$ 相距2个单位．点 $A ， B ， C$ 表示的数各是多少？

查看试题解析
22. 某班在一次数学兴趣活动中要分为四个组，已知第二组人数比第一组人数 $\frac{3}{2}$ 少5人，第三组人数比第一组与第二组人数的和少15人，第四组人数与第一组人数的2倍的和是34，若设第一组有x人．

(1)、用含x的式子表示第二、三、四组的人数，把答案填在下表相应的位置．

第一组

第二组

第三组

第四组

x

(2)、该班的总人数是否可以为47人？若可以，请写出每组的具体人数；若不可以，请说明理由．

查看试题解析
23. 我们知道，有理数包括整数、有限小数和无限循环小数，事实上，所有的有理数都可以化为分数形式（整数可看作分母为1的分数），那么无限循环小数如何表示为分数形式呢？请看以下示例：例将 $0. \dot{7}$ 化为分数形式
由于 $0. \dot{7} = 0.7777 \dots$ ，设 $x = 0.7777 \dots$ ①

则 $10 x = 7.777 \dots$ ②

②-①得 $9 x = 7$ ，解得 $x = \frac{7}{9}$ ，于是得 $0. \dot{7} = \frac{7}{9}$ ．

同理可得 $0. \dot{3} = \frac{3}{9} = \frac{1}{3}$ ， $7. \dot{4} = 7 + 0. \dot{4} = 7 + \frac{4}{9} = \frac{67}{9}$

根据以上阅读，回答下列问题：（以下计算结果均用最简分数表示）

(1)、基础训练： $0. \dot{6} =$ ， $8. \dot{2} =$ ；

(2)、参考（1）中的方法，比较 $0. \dot{9}$ 与1的大小： $0. \dot{9}$ 1；（填“ $>$ ”、“ $<$ ”或“ $=$ ”）

(3)、将 $0. \dot{6} \dot{4}$ 化为分数形式，写出推导过程．

(4)、迁移应用： $0. \dot{1} 5 \dot{3} =$ ；（注： $0. \dot{1} 5 \dot{3} = 0.153153 \dots$ ）

查看试题解析
24. 探索新知：
如图1，射线OC在∠AOB的内部，图中共有3个角：∠AOB ， ∠AOC和∠BOC ，若其中有一个角的度数是另一个角度数的两倍，则称射线OC是∠AOB的“巧分线”．

(1)、一个角的平分线这个角的“巧分线”；(填“是”或“不是”)

(2)、如图2，若∠MPN＝α，且射线PQ是∠MPN的“巧分线”，则∠MPQ＝；(用含α的代数式表示出所有可能的结果)

(3)、当t为何值时，射线PM是∠QPN的“巧分线”；

(4)、若射线PM同时绕点P以每秒5°的速度逆时针旋转，并与PQ同时停止，请直接写出当射线PQ是∠MPN的“巧分线”时t的值．

查看试题解析

第一组	第二组	第三组	第四组
x