山西省吕梁市交城县2019-2020学年七年级下学期数学期中试卷
试卷更新日期:2021-03-22 类型:期中考试
一、单选题
-
1. 在实数中,是无理数的是( )A、 B、 C、 D、2. 下列图形中,线段PQ的长度表示点P到直线L的距离的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图, , ,点B,O,D在同一条直线上,则 的度数是( )
3. 如图, , ,点B,O,D在同一条直线上,则 的度数是( )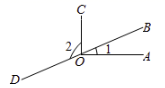 A、 B、 C、 D、4. 的算术平方根是( )A、±4 B、±2 C、4 D、25. 如图,在下列四组条件中,能得到 的是( )
A、 B、 C、 D、4. 的算术平方根是( )A、±4 B、±2 C、4 D、25. 如图,在下列四组条件中,能得到 的是( )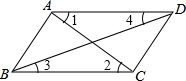 A、 B、 C、 D、6. 点P到x轴的距离是2,到y轴的距离是3,且点P在y轴的右侧,则P点的坐标是( )A、(2,3) B、(3,2)或(3,﹣2) C、(3,2) D、(2,3)或(2,﹣3)7. 点P( )在平面直角坐标系的y轴上,则点P的坐标为( )A、(0,2) B、(2,0) C、(0,-2) D、(0,-4)8. 如图,把一个长方形纸片沿 折叠后,点D、C分别落在 、 的位置,若 ,则 等于( )
A、 B、 C、 D、6. 点P到x轴的距离是2,到y轴的距离是3,且点P在y轴的右侧,则P点的坐标是( )A、(2,3) B、(3,2)或(3,﹣2) C、(3,2) D、(2,3)或(2,﹣3)7. 点P( )在平面直角坐标系的y轴上,则点P的坐标为( )A、(0,2) B、(2,0) C、(0,-2) D、(0,-4)8. 如图,把一个长方形纸片沿 折叠后,点D、C分别落在 、 的位置,若 ,则 等于( )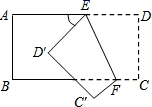 A、 B、 C、 D、9. 如图,直线 被直线 所截,且 ,过 上的点A作AB⊥ 交 于点B,其中∠1<30°,则下列一定正确的是( )
A、 B、 C、 D、9. 如图,直线 被直线 所截,且 ,过 上的点A作AB⊥ 交 于点B,其中∠1<30°,则下列一定正确的是( )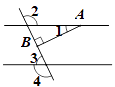 A、∠2>120° B、∠3<60° C、∠4-∠3>90° D、2∠3>∠410. 在平面直角坐标系 中,对于点 ,我们把点 叫做点P的伴随点.已知点 的伴随点为 ,点 的伴随点为 ,点 的伴随点为 ,…,这样依次得到点 .若点 的坐标为 ,则点 的坐标为( )A、 B、 C、 D、
A、∠2>120° B、∠3<60° C、∠4-∠3>90° D、2∠3>∠410. 在平面直角坐标系 中,对于点 ,我们把点 叫做点P的伴随点.已知点 的伴随点为 ,点 的伴随点为 ,点 的伴随点为 ,…,这样依次得到点 .若点 的坐标为 ,则点 的坐标为( )A、 B、 C、 D、二、填空题
-
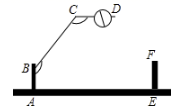
11. 的倒数是.12. 一个小区大门的栏杆如图所示, 垂直地面 于A, 平行于地面 ,那么 .
 13. 若 +|b2﹣1|=0,则ab= .14. 如图,在长20米,宽10米的长方形草地内修建了宽2米的道路,则道路的面积为 .
13. 若 +|b2﹣1|=0,则ab= .14. 如图,在长20米,宽10米的长方形草地内修建了宽2米的道路,则道路的面积为 .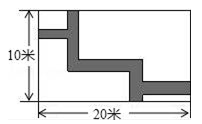 15. 已知点P的坐标为 并且满足点P到两坐标轴的距离相等,则点P的坐标是 .16. 已知: , , , ,…,根据上面各式的规律,等式 中口里应填的数是 .
15. 已知点P的坐标为 并且满足点P到两坐标轴的距离相等,则点P的坐标是 .16. 已知: , , , ,…,根据上面各式的规律,等式 中口里应填的数是 .三、解答题
-
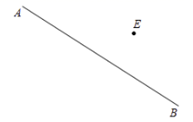
17. 计算:求下列等式中未知数x的值:(1)、 ;(2)、 .18. 已知正数x的两个不同的平方根分别是a+3和2a﹣15,且 =4.求x﹣2y+2的值.19. 如图,已知点E在直线 外.
 (1)、读下面语句,并用三角板与直尺画出图形.
(1)、读下面语句,并用三角板与直尺画出图形.①过E作直线 ,使 ;
②过E作直线 ,使 ,垂足为F.
(2)、根据(1)中所画图形,解答问题:请判断直线 与 的位置关系,并说明理由.20. 完成下面的求解过程:如图,已知BC∥DE,∠1=∠3,∠DFG=60°,求∠BDC的度数.
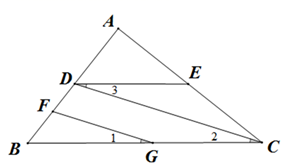
解:∵BC∥DE(已知)
∴∠2= ▲ . ( ▲ )
∵∠1=∠3,
∴∠1=∠2. ( ▲ )
∴DC∥ ▲ . ( ▲ )
∴∠DFG+ ▲ =180° . ( ▲ )
又∵∠DFG=60°
∴∠BDC= ▲ .
21. 如图, 中, , , , 是 平移之后得到的图形,并且 的对应点 的坐标为 .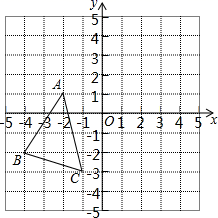 (1)、 点的坐标是;(2)、画出 平移之后的图形 ;(3)、求 的面积.22. 如图,直线 和直线 相交于点O, ,垂足为O, 平分 .
(1)、 点的坐标是;(2)、画出 平移之后的图形 ;(3)、求 的面积.22. 如图,直线 和直线 相交于点O, ,垂足为O, 平分 .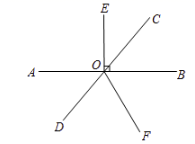 (1)、若 ,求 的度数;(2)、若 ,求 的度数.23. (阅读材料)
(1)、若 ,求 的度数;(2)、若 ,求 的度数.23. (阅读材料)数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:求59319的立方根.华罗庚脱口而出:“39”.邻座的乘客十分惊奇,忙间其中计算的奥妙.
你知道怎样迅速准确的计算出结果吗?请你按下面的步骤试一试:
第一步:∵ , , ,
∴ .
∴能确定59319的立方根是个两位数.
第二步:∵59319的个位数是9,
∴能确定59319的立方根的个位数是9.
第三步:如果划去59319后面的三位319得到数59,
而 ,则 ,可得 ,
由此能确定59319的立方根的十位数是3,因此59319的立方根是39.
(解答问题)
根据上面材料,解答下面的问题
(1)、求110592的立方根,写出步骤.(2)、填空: .24. 如图,已知 ,且 ,点C是射线 上一动点(不与点A重合), , 分别平分 和 .交射线 于点B,D.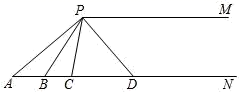 (1)、求 的度数;(2)、当点C运动到使 时,求 的度数;(3)、在点C运动过程中, 与 之间是否存在一定数量关系?若存在,请写出它们之间的数量关系,并说明理由;若不存在,请举出反例.
(1)、求 的度数;(2)、当点C运动到使 时,求 的度数;(3)、在点C运动过程中, 与 之间是否存在一定数量关系?若存在,请写出它们之间的数量关系,并说明理由;若不存在,请举出反例.