浙江省宁波市北仑区2020-2021学年七年级上学期数学期末考试试卷
试卷更新日期:2021-03-22 类型:期末考试
一、单选题
-
1. 下列四个数中,最小的数是( )A、0 B、 C、5 D、-12. 今年受新冠疫情的影响,各国经济都遭受了沉重的打击,但我国在全国人民的共同努力下走过了最艰难的时期,下半年迎来了经济的复苏,宁波今年的GDP便可达到1.23万亿.文中的数1.23万亿用科学记数法表示为( )A、 B、 C、 D、3. 下列说法中,正确的是( )A、零是最小的有理数 B、 一定是负数 C、正数的绝对值是它本身 D、如果两数积为正数,那么这两个数一定都是正数4. 的相反数,倒数分别是( )A、5; B、5; C、 ;5 D、5;55. 下列各组单项式中是同类项的是( )A、 和 B、3和 C、 和 D、 和6. 下列各数: , , , ,1.21221……(每两个1之间依次多一个2)中,无理数有( )A、2个 B、3个 C、4个 D、5个7. 一辆客车和一辆卡车同时从A地出发沿同一公路同方向行驶,客车的行驶速度是 ,卡车的行驶速度是 ,客车比卡车早40分钟经过B地.设A、B两地间的路程是 ,由题意可得方程( )A、 B、 C、 D、8. 如图,数轴上A , B , C三点所表示的数分别为a , b , c , 且 .如果有 ,那么该数轴原点0的位置应该在( )
 A、点A的左边 B、点A与B之间 C、点B与C之间 D、点C的右边9. 如图,把两张面积分别为9和4的小正方形卡片不重叠地放在一个大长方形中,未被卡片覆盖的阴影部分的周长为16,那么这个大长方形的面积为( )
A、点A的左边 B、点A与B之间 C、点B与C之间 D、点C的右边9. 如图,把两张面积分别为9和4的小正方形卡片不重叠地放在一个大长方形中,未被卡片覆盖的阴影部分的周长为16,那么这个大长方形的面积为( ) A、18 B、20 C、24 D、2510. 如图,点Q在线段 上,其中 ,第一次分别取线段 和 的中点 , 得到线段 ;再分别取线段 和 的中点 , 得到线段 ;第三次分别取线段 和 的中点 , 得到线段 ;连续这样操作11次,则每次的两个中点所形成的所有线段之和 ( )
A、18 B、20 C、24 D、2510. 如图,点Q在线段 上,其中 ,第一次分别取线段 和 的中点 , 得到线段 ;再分别取线段 和 的中点 , 得到线段 ;第三次分别取线段 和 的中点 , 得到线段 ;连续这样操作11次,则每次的两个中点所形成的所有线段之和 ( )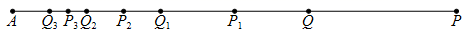 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 一袋糖果包装上印有“总质量 ”的字样.小明拿去称了一下,发现质量为 ,则该糖果厂家(填“有”或“没有”)欺诈行为.12. 多项式2x3﹣x2y2﹣1是次项式.13. 64的平方根是;64的立方根是 .14. 若 ,则 的值为 .15. 如图,一组数据按图中规律从左向右依次排列,则第11个图中 .
 16. 如图1, 为一条拉直的细线,长为 ,A、B两点在 上且 ,点A在点B的左侧.若先握住点B , 将 折向 ,使得 重叠在 上,如图2.再从图2的A点及与A点重叠处一起剪开 , 使得细线分成三段.若这三段的长度由短到长之比为1∶3∶4,其中以点P为一端的那段细线最长,则 的长为 .
16. 如图1, 为一条拉直的细线,长为 ,A、B两点在 上且 ,点A在点B的左侧.若先握住点B , 将 折向 ,使得 重叠在 上,如图2.再从图2的A点及与A点重叠处一起剪开 , 使得细线分成三段.若这三段的长度由短到长之比为1∶3∶4,其中以点P为一端的那段细线最长,则 的长为 .
三、解答题
-
17. 计算:(1)、(2)、18. 先化简,再求值: ,其中 , .19. 解下列一元一次方程:(1)、 ;(2)、 .20. 杨梅生津止渴营养丰富,深受人们的喜爱.宁波是杨梅的产地之一,某果农摘了5筐杨梅,若塑料筐质量忽略不计,每筐杨梅以 为标准,超过的千克数记为正数,不足的千克数记为负数,记录如下
 (1)、这5筐杨梅中,质量最大的一筐是 ,它比质量最小的一筐重 .(2)、这5筐杨梅的总质量为多少千克?若每千克杨梅售价为15元,则这5筐杨梅的总价为多少元?21. 如图,直线 与 交于点O , 垂足为O , 平分 .
(1)、这5筐杨梅中,质量最大的一筐是 ,它比质量最小的一筐重 .(2)、这5筐杨梅的总质量为多少千克?若每千克杨梅售价为15元,则这5筐杨梅的总价为多少元?21. 如图,直线 与 交于点O , 垂足为O , 平分 . (1)、若 ,求 和 的度数;(2)、若 ,则 . (用含 的代数式表示)22. 盲盒近来火爆,这种不确定的“盲抽”模式受到了大家的喜爱,某玩具商店计划采购文具盲盒和Molly盲盒,计划采购两种盲盒共125盒,这两种盲盒的进价、售价如下表:
(1)、若 ,求 和 的度数;(2)、若 ,则 . (用含 的代数式表示)22. 盲盒近来火爆,这种不确定的“盲抽”模式受到了大家的喜爱,某玩具商店计划采购文具盲盒和Molly盲盒,计划采购两种盲盒共125盒,这两种盲盒的进价、售价如下表:类型
进价(元/盒)
售价(元/盒)
文具盲盒
16
20
Molly盲盒
36
52
(1)、若采购共用去4000元,则两种盲盒各采购了多少盒?(2)、在(1)的条件下全部售完这125盒,那么玩具商店获利多少元?(3)、销售完这125个盲盒的总利润能否恰好为1600元?若能,请说出釆购方案;若不能,说明理由.23. 如图1,把两个边长为1的小正方形沿对角线剪开,所得的4个直角三角形拼成一个面积为2的大正方形.由此得到了一种能在数轴上画出无理数对应点的方法.
 (1)、图2中A、B两点表示的数分别为 , ;(2)、请你参照上面的方法:
(1)、图2中A、B两点表示的数分别为 , ;(2)、请你参照上面的方法:①把图3中 的长方形进行剪裁,并拼成一个大正方形.在图3中画出裁剪线,并在图4的正方形网格中画出拼成的大正方形,该正方形的边长 . (注:小正方形边长都为1,拼接不重叠也无空隙)
②在①的基础上,参照图2的画法,在数轴上分别用点M、N表示数a以及 .(图中标出必要线段的长)
 24. 如图1,点O在直线 上,过点O引一条射线 ,使 ,将一个直角三角尺的直角顶点放在点O处,直角边 在射线 上,另一边 在直线 的下方.
24. 如图1,点O在直线 上,过点O引一条射线 ,使 ,将一个直角三角尺的直角顶点放在点O处,直角边 在射线 上,另一边 在直线 的下方.(操作一):将图1中的三角尺绕着点O以每秒 的速度按顺时针方向旋转.当它完成旋转一周时停止,设旋转的时间为t秒.
 (1)、 的度数是 , 图1中与它互补的角是 .(2)、三角尺旋转的度数可表示为(用含t的代数式表示):当 时, .(3)、(操作二):如图2将一把直尺的一端点也放在点O处,另一端点E在射线 上.如图3,在三角尺绕着点O以每秒 的速度按顺时针方向旋转的同时,直尺也绕着点O以每秒 的速度按顺时针方向旋转,当一方完成旋转一周时停止,另一方也停止旋转,设旋转的时间为t秒.
(1)、 的度数是 , 图1中与它互补的角是 .(2)、三角尺旋转的度数可表示为(用含t的代数式表示):当 时, .(3)、(操作二):如图2将一把直尺的一端点也放在点O处,另一端点E在射线 上.如图3,在三角尺绕着点O以每秒 的速度按顺时针方向旋转的同时,直尺也绕着点O以每秒 的速度按顺时针方向旋转,当一方完成旋转一周时停止,另一方也停止旋转,设旋转的时间为t秒.
当t为何值时, ,并说明理由?(4)、试探索:在三角尺与直尺旋转的过程中,当 ,是否存在某个时刻,使得 与 中其中一个角是另一个角的两倍?若存在,请求出所有满足题意的t的值;若不存在,请说明理由.