浙江省杭州市下城区2020-2021学年七年级上学期数学期末考试试卷
试卷更新日期:2021-03-22 类型:期末考试
一、单选题
-
1. 下列各数中,最大的数是( )A、2 B、-2 C、 D、2. 下列选项中,结果小于-1的是( )A、 B、 C、 D、3. 若 , 均为整数,且 ,则 不可能是( )A、正数 B、负数 C、无理数 D、实数4. 若 ,则下列各组数中,与 互为相反数的是( )A、 B、 C、 D、5. 设两个互余的锐角分别为 和 ,( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则6. 在计算 时,下列四个过程:①原式 ;②原式 ;③原式 ;④原式 ,其中正确的是( )A、① B、② C、③ D、④7. 设 , , 均为实数,且满足 ,( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则8. 如图,点 ,点 在线段 上,若 ,点 是 的中点,则( )
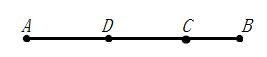 A、 B、 C、 D、9. 一个密封的长方体容器内装有部分水,液体部分的截面恰好是一个正方形(如图1),液面到容器顶端的距离是 .若把该容器横放(如图2),液面到容器顶端的距离是 .则这个容器的截面面积是( )
A、 B、 C、 D、9. 一个密封的长方体容器内装有部分水,液体部分的截面恰好是一个正方形(如图1),液面到容器顶端的距离是 .若把该容器横放(如图2),液面到容器顶端的距离是 .则这个容器的截面面积是( )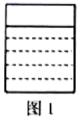
 A、 B、 C、 D、10. 对于实数 , ,定义运算“ ”满足: .若 ,则( )A、 B、 C、 D、
A、 B、 C、 D、10. 对于实数 , ,定义运算“ ”满足: .若 ,则( )A、 B、 C、 D、二、填空题
-
11. 若 ,且 是整数,则 .12. 若长方形的长是宽的3倍,面积是6,则它的宽是 .13. 若 ,则α的补角 . (用“度、分”表示).14. 已知 ,射线 , 在 内部, 平分 , 平分 ,则 °.15. 如图,在数轴上,点 ,点 表示的数分别是 ,10,点 以2个单位/秒的速度从 出发沿数轴向右运动,同时点 以3个单位/秒的速度从点 出发沿数轴在 , 之间往返运动.当点 到达点 时,点 表示的数是 .
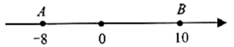 16. 若 ,其中 , 均为整数,则符合题意的有序数对 的组数是 .
16. 若 ,其中 , 均为整数,则符合题意的有序数对 的组数是 .三、解答题
-
17. 计算:(1)、 ;(2)、 .18. 解方程:(1)、 ;(2)、 .19. 先化简,再求值: ,其中 , .20. 青藏铁路线上,在格尔木到拉萨之间有一段很长的冻土地段,列车在冻土地段、非冻土地段的行驶速度分别是100千米/小时和120千米/小时.(1)、列车在冻土地段行驶时, 小时行驶多少千米(用含 的代数式表示)?(2)、在格尔木到拉萨路段,列车通过冻土地段比通过非冻土地段多用0.5小时,如果通过冻土地段需要 小时,则非冻土地段的长度是多少千米(用含 的代数式表示)?21. 在射线 上截取 ,点 是 的中点,点 是 的中点, .(1)、求 的长;(2)、设 为正整数,讨论 和 的大小.22. 已知 与 互补,射线 平分 ,设 , .
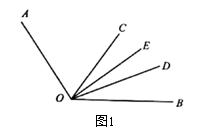
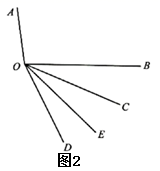 (1)、如图1, 在 的内部,
(1)、如图1, 在 的内部,①当 时,求 的值.
②当 时,求 的度数.
(2)、如图2, 在 的外部, ,求 与 满足的等量关系.23. 某景区门票上绘制了简易游览图(如图),从游客中心到观景台有 山路,从观景台到山顶有 山路,圆圆同学从导游口中得知:离观景台 处有一个凉亭,离凉亭 处有一个小卖部.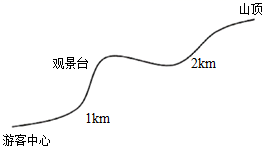 (1)、圆圆同学把这张图中的游览线路抽象成一条数轴,其中游客中心是原点,往山顶方向为正方向, 为1个单位长度,请在数轴上标出小卖部 所有可能的位置,并用数字表示出来.
(1)、圆圆同学把这张图中的游览线路抽象成一条数轴,其中游客中心是原点,往山顶方向为正方向, 为1个单位长度,请在数轴上标出小卖部 所有可能的位置,并用数字表示出来. (2)、圆圆同学上山时从游客中心到山顶共用了 小时,下山时从山顶到游客中心的平均速度为 千米/小时,求圆圆同学上山、下山全程的平均速度(用含 和 的代数式表示).(3)、若凉亭在观景台到山顶的途中,方方同学上午 从游客中心出发匀速上山,于 到达观景台,在观景台停留30分钟后,以同样的速度继续上山,途中又在凉亭休息了15分钟,到山顶游玩了35分钟后下山(下山途中不再停留),为了在下午 准时回到游客中心,方方同学下山的速度比上山的速度快 ,求 的值.
(2)、圆圆同学上山时从游客中心到山顶共用了 小时,下山时从山顶到游客中心的平均速度为 千米/小时,求圆圆同学上山、下山全程的平均速度(用含 和 的代数式表示).(3)、若凉亭在观景台到山顶的途中,方方同学上午 从游客中心出发匀速上山,于 到达观景台,在观景台停留30分钟后,以同样的速度继续上山,途中又在凉亭休息了15分钟,到山顶游玩了35分钟后下山(下山途中不再停留),为了在下午 准时回到游客中心,方方同学下山的速度比上山的速度快 ,求 的值.