浙江省杭州市西湖区2020-2021学年七年级上学期数学期末考试试卷

试卷更新日期：2021-03-22 类型：期末考试

进入出卷网下载

一、单选题

1. -2021的相反数是（）

A、-2021 B、2021 C、 $- \frac{1}{2021}$ D、 $\frac{1}{2021}$

查看试题解析
2. 浙教版初中数学课本封面长度约为26.0厘米，是精确到（）

A、1毫米 B、1厘米 C、1分米 D、1米

查看试题解析
3. 2020年我国武汉暴发新冠肺炎疫情，全国人民发扬“一方有难.八方支援”的精神，积极参与到武汉防疫抗疫保卫战中.据统计，参与到武汉防疫抗疫中的全国医护人员约为42000人，将42000这个数用科学记数法表示正确的是（）

A、 $42 \times 10^{3}$ B、 $4.2 \times 10^{4}$ C、 $0.42 \times 10^{5}$ D、 $4.2 \times 10^{3}$

查看试题解析
4. 下列计算正确的是（）

A、 $a^{3} - a^{2} = a$ B、 $a^{6} \div a^{2} = a^{3}$ C、 $a^{6} - a^{2} = a^{4}$ D、 $a^{3} \div a^{2} = a$

查看试题解析
5. 若 $4 x = 3 y + 2$ ，则下列式子正确的是（）

A、 $8 x + 6 y = 4$ B、 $8 x - 4 = 6 y$ C、 $4 x + y = 3 y + x + 2$ D、 $6 x - 8 y = 4$

查看试题解析
6. 如图，点A表示的实数是a ，则下列判断正确的是（）

A、 $a - 1 > 0$ B、 $a + 1 < 0$ C、 $a - 1 < 0$ D、 $| a | > 1$

查看试题解析
7. 关于 $\sqrt{8}$ 的叙述，正确的是（）

A、 $\sqrt{8}$ 是有理数 B、面积为4的正方形边长是 $\sqrt{8}$ C、 $\sqrt{8}$ 是无限不循环小数 D、在数轴上找不到可以表示 $\sqrt{8}$ 的点

查看试题解析
8. 已知点 $A$ 、 $B$ 、 $P$ 在一条直线上，则下列等式中，能判断 $P$ 是线段 $A B$ 的中点的是（）

A、 $A P = B P$ B、 $B P = \frac{1}{2} A B$ C、 $A B = 2 A P$ D、 $A P + P B = A B$

查看试题解析
9. 如图，将一副三角板叠在一起使直角顶点重合于点O ，（两块三角板可以在同一平面内自由转动，且 $∠ B O D$ ， $∠ A O C$ 均小于180°），下列结论一定成立的是（）

A、 $∠ B O D > ∠ A O C$ B、 $∠ B O D - ∠ A O C = 90^{\circ}$ C、 $∠ B O D + ∠ A O C = 180^{\circ}$ D、 $∠ B O D \neq ∠ A O C$

查看试题解析
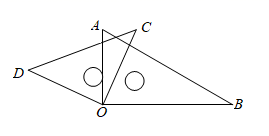10. 学校在一次研学活动中，有n位师生乘坐m辆客车，若每辆客车乘50人，则还有12人不能上车；若每辆客车乘55人，则最后一辆车空了13个座位．下列四个等式：
① $50 m + 12 = 55 m - 13$ ；② $50 m - 12 = 55 m + 13$ ；③ $\frac{n - 12}{50} = \frac{n + 13}{55}$ ；④ $\frac{n + 12}{50} = \frac{n - 13}{55}$ ．

其中正确的是（）

A、①② B、①③ C、③④ D、①④

查看试题解析

二、填空题

11. 3的平方根是

查看试题解析
12. 若 $∠ A = 40^{\circ} 17'$ ，则 $∠ A$ 的补角的度数为．

查看试题解析
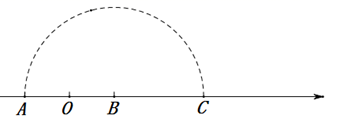
13. 若 $2^{n} - 1 = 6$ ，则 $4 \times 2^{n} - 4 =$ ．

查看试题解析
14. 如图，点A ， B在数轴上，点O为原点， $O A = O B$ .按如图所示方法用圆规在数轴上截取 $B C = A B$ ，若点C表示的数是15，则点A表示的数是．

查看试题解析
15. 某快递公司在市区的收费标准为：寄一件物品，不超过1千克付费10元；超出1千克的部分加收2元/千克．乐乐在该公司寄市区内的一件物品，重x（ $x > 1$ ）千克，则需支付元．（用含x的代数式表示）

查看试题解析
16. 对于三个互不相等的有理数a ， b ， c ，我们规定符号 $\max {a ， b ， c}$ 表示a ， b ， c三个数中较大的数，例如 $\max {2 ， 3 ， 4} = 4$ .按照这个规定则方程 $\max {x ， - x ， 0} = 3 x - 2$ 的解为．

查看试题解析

三、解答题

17. 计算：

(1)、 $(- \frac{3}{4}) - (- \frac{1}{6}) + (- \frac{5}{4}) - \frac{5}{6}$ ；

(2)、 $\sqrt[3]{- 27} - 8 \div {(- 2)}^{2}$ ．

查看试题解析
18. 解方程：

(1)、 $3 x + 2 (1 - x) = - 4 (1 - x)$ ；

(2)、 $\frac{2 x - 1}{3} = 1 - \frac{5 x - 2}{6}$ ．

查看试题解析
19. 1号探测气球从海拔2m处出发，以0.6m/s的速度匀速上升．与此同时，2号探测气球从海拔8m处出发，以0.4m/s的速度匀速上升．

(1)、经x秒后，求1号、2号探测气球的海拔高度（用含x的代数式表示）；

(2)、出发多长时间1号探测气球与2号探测气球的海拔高度相距4m．

查看试题解析
20. 在平面内有三点A ， B ， C ．

(1)、如图，作出A ， C两点之间的最短路线；在射线BC上找一点D ，使线段AD长最短；

(2)、若A ， B ， C三点共线，若 $A B = 20 cm$ ， $B C = 14 cm$ ，点E ， F分别是线段AB ， BC的中点，求线段EF的长．

查看试题解析
21. 如图在某居民区规划修建一个小广场（图中阴影部分）．

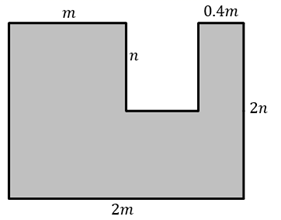(1)、用含m ， n的代数式分别表示该广场的周长C与面积S；

(2)、当 $m = 6$ 米， $n = 5$ 米时，分别求该广场的周长和面积．

查看试题解析
22. 已知点A ， B ， O在一条直线上，以点O为端点在直线AB的同一侧作射线 $O C$ ， $O D$ ， $O E$ 使 $∠ B O C = ∠ E O D = 60^{\circ}$ ．

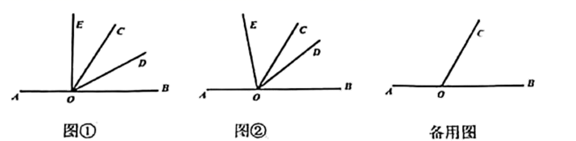(1)、如图①，若 $O D$ 平分 $∠ B O C$ ，求 $∠ A O E$ 的度数；

(2)、如图②，将 $∠ E O D$ 绕点O按逆时针方向转动到某个位置时，使得 $O D$ 所在射线把 $∠ B O C$ 分成两个角．
①若 $∠ C O D ： ∠ B O D = 1 ： 2$ ，求 $∠ A O E$ 的度数；

②若 $∠ C O D ： ∠ B O D = 1 ： n$ （n为正整数），直接用含n的代数式表示 $∠ A O E$ ．

查看试题解析
23. 如图，数轴上有A ， B两点，A在B的左侧，表示的有理数分别为a ， b ，已知 $A B = 12$ ，原点O是线段AB上的一点，且 $O A = 5 O B$ ．

(1)、求a ， b的值；

(2)、若动点P ， Q分别从A ， B同时出发，向数轴正方向匀速运动，点P的速度为每秒2个单位长度，点Q的速度为每秒1个单位长度，设运动时间为t秒，当点P与点Q重合时，P ， Q重两点停止运动，当t为何值时， $2 O P - O Q = 3$ ；

(3)、在（2）的条件下，若当点P开始运动时，动点M从点A出发，以每秒3个单位长度的速度也向数轴正方向匀速运动，当点M追上点Q后立即返回，以同样的速度向点P运动，遇到点P后点M就停止运动．求点M停止时，点M在数轴上所对应的数．

查看试题解析