辽宁省营口市2019-2020学年七年级下学期数学期中试卷
试卷更新日期:2021-03-22 类型:期中考试
一、单选题
-
1. 下列各图中,∠1和∠2是对顶角的是( )A、
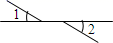 B、
B、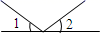 C、
C、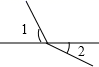 D、
D、 2. 4的算术平方根是( )A、-2 B、2 C、 D、3. 甲骨文是我国的一种古代文字,是汉字的早期形式,下列甲骨文中,能用其中一部分平移得到的是( )A、
2. 4的算术平方根是( )A、-2 B、2 C、 D、3. 甲骨文是我国的一种古代文字,是汉字的早期形式,下列甲骨文中,能用其中一部分平移得到的是( )A、 B、
B、 C、
C、 D、
D、 4. 如图是小凡同学在体育课上跳远后留下的脚印,他的跳远成绩是线段( )的长.
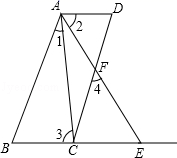
4. 如图是小凡同学在体育课上跳远后留下的脚印,他的跳远成绩是线段( )的长.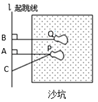 A、 B、 C、 D、5. 已知 与 互为补角, ,则 的余角的度数为( )A、 B、 C、 D、6. 在 ,3.33, , ,0.04445555⋯, ,127, 中,无理数的个数有( )A、2个 B、3个 C、4个 D、5个7. 如图,点E在AD的延长线上,下列条件中能判断BC∥AD的是( )
A、 B、 C、 D、5. 已知 与 互为补角, ,则 的余角的度数为( )A、 B、 C、 D、6. 在 ,3.33, , ,0.04445555⋯, ,127, 中,无理数的个数有( )A、2个 B、3个 C、4个 D、5个7. 如图,点E在AD的延长线上,下列条件中能判断BC∥AD的是( )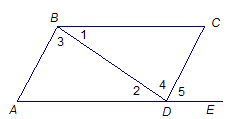 A、∠3=∠4 B、∠A+∠ADC=180° C、∠1=∠2 D、∠A=∠58. 平面直角坐标系内有一点P(-2020,-2020),则点P在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 如图,三角板的直角顶点放在直线b上,已知a∥b,∠1=28°,则∠2的度数为( )
A、∠3=∠4 B、∠A+∠ADC=180° C、∠1=∠2 D、∠A=∠58. 平面直角坐标系内有一点P(-2020,-2020),则点P在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 如图,三角板的直角顶点放在直线b上,已知a∥b,∠1=28°,则∠2的度数为( )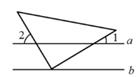 A、28° B、56° C、62° D、152°10. 如图,E,F分别是AB,CD上的点,G是BC的延长线上一点,且∠B=∠DCG=∠D,则下列结论不一定成立的是( )
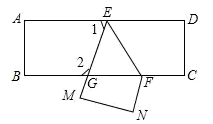
A、28° B、56° C、62° D、152°10. 如图,E,F分别是AB,CD上的点,G是BC的延长线上一点,且∠B=∠DCG=∠D,则下列结论不一定成立的是( ) A、∠AEF=∠EFC B、∠A=∠BCF C、∠AEF=∠EBC D、∠BEF+∠EFC=180°
A、∠AEF=∠EFC B、∠A=∠BCF C、∠AEF=∠EBC D、∠BEF+∠EFC=180°二、填空题
-
11. 如图直线AB、CD相交于点O,OE⊥AB,O为垂足,如果∠EOD=38°,则∠COB= .
 12. 一个小区大门的栏杆如图所示, 垂直地面 于A, 平行于地面 ,那么 .
12. 一个小区大门的栏杆如图所示, 垂直地面 于A, 平行于地面 ,那么 .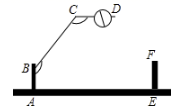 13. 把命题“对顶角相等”改写成“如果…那么…”的形式是.14. 某宾馆在重新装修后,准备在大厅的楼梯上铺上某种规格的红色地毯,其侧面如图,则至少需要购买地毯米.
13. 把命题“对顶角相等”改写成“如果…那么…”的形式是.14. 某宾馆在重新装修后,准备在大厅的楼梯上铺上某种规格的红色地毯,其侧面如图,则至少需要购买地毯米. 15. 的平方根是;-125的立方根是; 的值是 .16. 已知 、 为两个连续的整数,且 ,则17. 平面直角坐标系内,点P(3,﹣4)到y轴的距离是.18. 已知点A(a,0)和点B(0,5)两点,且直线AB与坐标轴围成的三角形的面积等于10,则a的值是.
15. 的平方根是;-125的立方根是; 的值是 .16. 已知 、 为两个连续的整数,且 ,则17. 平面直角坐标系内,点P(3,﹣4)到y轴的距离是.18. 已知点A(a,0)和点B(0,5)两点,且直线AB与坐标轴围成的三角形的面积等于10,则a的值是.三、解答题
-
19. 计算:(1)、( + )-(2)、3 +220. 利用平方根(或立方根)的概念解下列方程:(1)、9(x-3)2=64;(2)、(2x-1)3=-8.21. 如图,直线CD与直线AB相交于C,根据下列语句画图、解答.

⑴过点P作PQ∥CD,交AB于点Q;
⑵过点P作PR⊥CD,垂足为R;
⑶若∠DCB=120°,猜想∠PQC是多少度?并说明理由
22. 已知a-7和2a+4是某正数的两个平方根,b-7的立方根是1.(1)、求 的值;(2)、求 的算术平方根.23. 如图,AD⊥BC,垂足为D,点E、F分别在线段AB、BC上,EF⊥BC,∠CAD=∠DEF, (1)、求证:EF∥AD;(2)、判断ED与AC的位置关系,并证明你的猜想.24. 如图是某校的平面示意图,已知图书馆、行政楼的坐标分别为(-3,2),(2,3).完成以下问题:
(1)、求证:EF∥AD;(2)、判断ED与AC的位置关系,并证明你的猜想.24. 如图是某校的平面示意图,已知图书馆、行政楼的坐标分别为(-3,2),(2,3).完成以下问题: (1)、请根据题意在图上建立直角坐标系;(2)、写出图上其他四个地点实验楼、校门口、综合楼、信息楼的坐标;(3)、在图中用点P表示体育馆(-1,-3)的位置.
(1)、请根据题意在图上建立直角坐标系;(2)、写出图上其他四个地点实验楼、校门口、综合楼、信息楼的坐标;(3)、在图中用点P表示体育馆(-1,-3)的位置.