江苏省苏州市昆山市2020-2021学年七年级上学期数学期末考试试卷
试卷更新日期:2021-03-22 类型:期末考试
一、单选题
-
1. -2的相反数是( )A、-2 B、 C、2 D、2. 疫情期间,我市红十字会累计接收社会各界爱心人士捐赠口罩、隔离衣、手套等88批次物资,价值约为5100000万元,则用5100000科学记数法可表示为( )A、 B、 C、 D、3. 下列计算结果正确的是( )A、 B、 C、 D、4. 下列方程中,解为 的是( )A、 B、 C、 D、5. 下列平面图形中,经过折叠能围成一个正方体的是( )A、
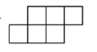 B、
B、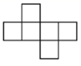 C、
C、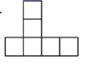 D、
D、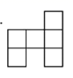 6. 若 与 的差是一个单项式,则代数式 的值为( )A、-8 B、9 C、-9 D、-67. 若关于 的方程 的解是 ,则代数式 的值为( )A、-6 B、0 C、12 D、188. 下列说法正确的是( )A、具有公共顶点的两个角是对顶角 B、 两点之间的距离就是线段 C、两点之间,线段最短 D、不相交的两条直线叫做平行线9. 《九章算术》是我国古代数学名著,卷7“盈不足”中有题译文如下:现有一伙人共同买一个物品,每人出8钱,还余3钱;每人出 钱,还差4钱,问有人数、物价各是多少?设物价为 钱,根据题意可列出方程( )A、 B、 C、 D、10. 如图,在长方形 中, , ,点 是 上的点,且 .点 从点 出发,以 的速度沿点 匀速运动,最终到达点 .设点 运动时间为 ,若三角形 的面积为 ,则 的值为( )
6. 若 与 的差是一个单项式,则代数式 的值为( )A、-8 B、9 C、-9 D、-67. 若关于 的方程 的解是 ,则代数式 的值为( )A、-6 B、0 C、12 D、188. 下列说法正确的是( )A、具有公共顶点的两个角是对顶角 B、 两点之间的距离就是线段 C、两点之间,线段最短 D、不相交的两条直线叫做平行线9. 《九章算术》是我国古代数学名著,卷7“盈不足”中有题译文如下:现有一伙人共同买一个物品,每人出8钱,还余3钱;每人出 钱,还差4钱,问有人数、物价各是多少?设物价为 钱,根据题意可列出方程( )A、 B、 C、 D、10. 如图,在长方形 中, , ,点 是 上的点,且 .点 从点 出发,以 的速度沿点 匀速运动,最终到达点 .设点 运动时间为 ,若三角形 的面积为 ,则 的值为( )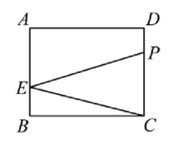 A、 或 B、 或 或 C、 或6 D、6或 或
A、 或 B、 或 或 C、 或6 D、6或 或二、填空题
-
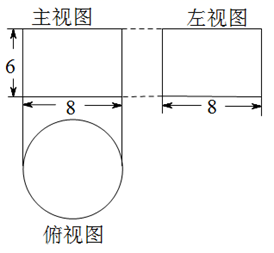
11. 比0小3的数是 .12. 单项式 的次数为 .13. 用代数式表示: 的 倍与 的和的立方为 .14. 一个几何体的三视图如图所示,则它的体积是 . (结果保留 )
 15. 已知直线 与直线 相交于点 , ,垂足为 .若 ,则 的度数为 . (单位用度表示)
15. 已知直线 与直线 相交于点 , ,垂足为 .若 ,则 的度数为 . (单位用度表示)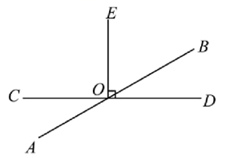 16. 钟表上显示6时20分,则此刻时针与分针的夹角的度数为 .17. 在数的学习中,我们会对其中一些具有某种特质的数进行研究,如学习自然数时,我们研究了奇数、偶数、质数、合数等.现在我们来研究一种特殊的数——巧数.定义:若一个两位数恰等于它的各位数字之和的4倍,则这个两位数称为巧数.若一个巧数的个位数字比十位数字大3,则这个巧数是 .18. 如图所示的图形都是由大小相同的黑点按照一定规律所组成的,其中第①个图形中一共有 个黑点,第②个图形中一共有5个黑点,第③个图形中一共有13个黑点,…,按此规律排列下去,第 个图形中黑点的个数为 . (用含 的代数式表示)
16. 钟表上显示6时20分,则此刻时针与分针的夹角的度数为 .17. 在数的学习中,我们会对其中一些具有某种特质的数进行研究,如学习自然数时,我们研究了奇数、偶数、质数、合数等.现在我们来研究一种特殊的数——巧数.定义:若一个两位数恰等于它的各位数字之和的4倍,则这个两位数称为巧数.若一个巧数的个位数字比十位数字大3,则这个巧数是 .18. 如图所示的图形都是由大小相同的黑点按照一定规律所组成的,其中第①个图形中一共有 个黑点,第②个图形中一共有5个黑点,第③个图形中一共有13个黑点,…,按此规律排列下去,第 个图形中黑点的个数为 . (用含 的代数式表示)
三、解答题
-
19. 计算;(1)、(2)、20. 解下列方程:(1)、(2)、21. 已知,其中 ,其中 ,(1)、 , ;(2)、求 的值.22. 在如图所示的方格纸中,每个小正方形的顶点称为格点,点 都在格点上.
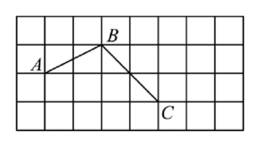 (1)、找一格点 ,使得直线 ,画出直线 ;(2)、找一格点 ,使得直线 于点 ,画出直线 ,并注明垂足 ;(3)、找一格点 ,使得直线 ,画出直线 ;(4)、连接 ,则线段 的大小关系是(用“ ”连接).23. 如图,已知点 是线段 上一点,点 是线段 的中点,若 ,
(1)、找一格点 ,使得直线 ,画出直线 ;(2)、找一格点 ,使得直线 于点 ,画出直线 ,并注明垂足 ;(3)、找一格点 ,使得直线 ,画出直线 ;(4)、连接 ,则线段 的大小关系是(用“ ”连接).23. 如图,已知点 是线段 上一点,点 是线段 的中点,若 ,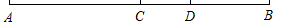 (1)、求线段 的长;(2)、若点 是直线 上一点,且 ,点 是 的中点,求线段 的长.24. 小明在对关于 的方程 去分母时,得到了方程 ,因而求得的解是 ,你认为他的答案正确吗?如果不正确,请求出原方程的正确解.25. 基本事实:已知过 两点可以画一条直线 ,我们得到了一个基本事实 , 若平面内有不在同一直线上的3个点,过其中任意两点,一共可以画条直线;
(1)、求线段 的长;(2)、若点 是直线 上一点,且 ,点 是 的中点,求线段 的长.24. 小明在对关于 的方程 去分母时,得到了方程 ,因而求得的解是 ,你认为他的答案正确吗?如果不正确,请求出原方程的正确解.25. 基本事实:已知过 两点可以画一条直线 ,我们得到了一个基本事实 , 若平面内有不在同一直线上的3个点,过其中任意两点,一共可以画条直线;类比:如图 ,已知 ,在AOB的内部画射线 ,则图中共有个角;
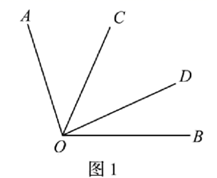
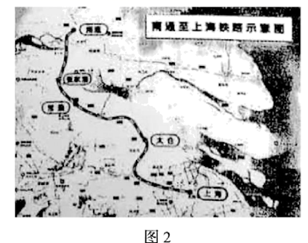
实践应用:2020年7月1日,沪苏通铁路正式通车,加快了长三角交通一体化建设,沪苏通铁路衔接南通和上海,并在沿途增设张家港、常熟、太仓三个停靠站,如图2.若一动车往返于上海与南通之间,已知各站之间的路程均不相等.则共有种不同的票价.(不考虑座位等级等其它因素)
 26. 新冠病毒疫情初期,口罩供应短缺,某口罩生产厂家接到一批口罩定制任务,要求10天完成.如果安排第一车间单独加工,则正好如期完成任务;如果安排第二车间单独加工,则会延期 天完成.(1)、为尽快完成任务,厂长安排第一车间单独加工5天后,随即安排第二车间加入一起加工,那么该厂家可以提前几天完成任务?(2)、已知第一车间一天投入生产的成本是1.2万元,第二车间一天投入生产的成本是0.7万元,现有三种加工方案:
26. 新冠病毒疫情初期,口罩供应短缺,某口罩生产厂家接到一批口罩定制任务,要求10天完成.如果安排第一车间单独加工,则正好如期完成任务;如果安排第二车间单独加工,则会延期 天完成.(1)、为尽快完成任务,厂长安排第一车间单独加工5天后,随即安排第二车间加入一起加工,那么该厂家可以提前几天完成任务?(2)、已知第一车间一天投入生产的成本是1.2万元,第二车间一天投入生产的成本是0.7万元,现有三种加工方案:方案一:第一车间单独加工;
方案二:第二车间单独加工;
方案三:两个车间同时加工.
如果你是厂长,在以上三种方案中,应选择哪一种方案安排生产,既可以节约成本,又在规定时间内完成这批口罩加工任务?请通过计算说明理由.
27. 数学实践课上,小明同学将直角三角板 的直角顶点 放在直尺 的边缘,将直角三角板绕着顶点 旋转.(1)、若三角板 在 的上方,如图1所示,在旋转过程中,小明发现 的大小发生了变化,但它们的和不变,即 ; (2)、若 分别位于 的上方和下方,如图2所示,则 之间的上述关系还成立吗?若不成立,则它们之间有怎样的数量关系?请说明你的理由;
(2)、若 分别位于 的上方和下方,如图2所示,则 之间的上述关系还成立吗?若不成立,则它们之间有怎样的数量关系?请说明你的理由;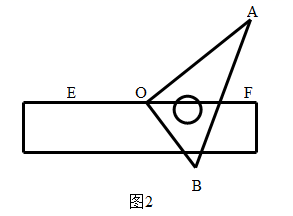 (3)、射线 分别是 的角平分线,若三角板 始终在 的上方,则旋转过程中, 的度数是一个定值吗?若是,请求出这个定值;若不是,请说明理由.
(3)、射线 分别是 的角平分线,若三角板 始终在 的上方,则旋转过程中, 的度数是一个定值吗?若是,请求出这个定值;若不是,请说明理由. 28. 已知数轴上有 两点,点 表示的数为-8,且 ,(1)、点 表示的数为;(2)、如图1,若点 在点 的右侧,点 以每秒4个单位的速度从点 出发向右匀速运动.
28. 已知数轴上有 两点,点 表示的数为-8,且 ,(1)、点 表示的数为;(2)、如图1,若点 在点 的右侧,点 以每秒4个单位的速度从点 出发向右匀速运动.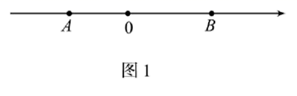
①若点 同时以每秒2个单位的速度从点 出发向左匀速运动,经过多少秒后,点 与点 相距 个单位.
②若点 同时以每秒2个单位的速度从点 出发向右匀速运动,经过多少秒后,在点 三点中,其中有一点是另外两个点连接所成线段的中点.