江苏省南京市鼓楼区2020-2021学年七年级上学期数学期末考试试卷
试卷更新日期:2021-03-22 类型:期末考试
一、单选题
-
1. 下列四个算式中,有一个算式与其他三个算式的计算结果不同,该算式是( )A、 B、 C、 D、2. 与 是同类项的是( )A、 B、 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. 在下列日常生活的操作中,能体现基本事实“两点之间,线段最短”的是( )A、用两颗钉子可以固定一根木条 B、把弯路改直可以缩短路程 C、用两根木桩拉一直线可把树栽成一排 D、沿桌子的一边看,可将桌子排整齐5. 下列图形中,线段 的长表示点A到直线 距离的是( )A、
 B、
B、 C、
C、 D、
D、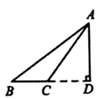 6. 如图是一个圆,一只电子跳蚤在标有数字的五个点上跳跃.若它停在奇数点上时,则下一次沿顺时针方向跳两个点;若停在偶数点上时,则下一次沿逆时针方向跳一个点.若这只跳蚤从 这点开始跳,则经过 次跳跃后它所停在的点对应的数为( )
6. 如图是一个圆,一只电子跳蚤在标有数字的五个点上跳跃.若它停在奇数点上时,则下一次沿顺时针方向跳两个点;若停在偶数点上时,则下一次沿逆时针方向跳一个点.若这只跳蚤从 这点开始跳,则经过 次跳跃后它所停在的点对应的数为( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
7. -5的相反数是 .8. 国家统计局刚刚发布数据,初步核算, 年全年国内生产总值为 亿元,将 科学记数法可以表示为 .9. 写出一个比 大的无理数:.10. 已知 ,则 的补角是.11. 下图是一位同学数学笔记可见的一部分.若要补充文中这个不完整的代数式,你补充的内容是: .
 12. 传统文化与创意营销的结合使已有近600年历史的故宫博物院重新焕发出生机,一些文创产品让顾客爱不释手.某购物网站上销售故宫文创笔记本和珐琅书签,若文创笔记本的销量比珐琅书签销量的2倍少700件,二者销量之和为5900件,用x表示珐琅书签的销量,则可列出一元一次方程 .13. 如图,直线 、 相交于点 ,将量角器的中心与点 重合,发现表示 的点在直线 上,表示 的点在直线 上,则 .
12. 传统文化与创意营销的结合使已有近600年历史的故宫博物院重新焕发出生机,一些文创产品让顾客爱不释手.某购物网站上销售故宫文创笔记本和珐琅书签,若文创笔记本的销量比珐琅书签销量的2倍少700件,二者销量之和为5900件,用x表示珐琅书签的销量,则可列出一元一次方程 .13. 如图,直线 、 相交于点 ,将量角器的中心与点 重合,发现表示 的点在直线 上,表示 的点在直线 上,则 .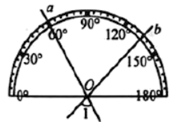 14. 如图,将一刻度尺放在数轴上(数轴的单位长度是1cm),刻度尺上表示“0cm”、“8cm”的点分别对应数轴上的﹣2和x , 那么x的值为 .
14. 如图,将一刻度尺放在数轴上(数轴的单位长度是1cm),刻度尺上表示“0cm”、“8cm”的点分别对应数轴上的﹣2和x , 那么x的值为 . 15. 如图,将一个三角板 角的顶点与另一个三角板的直角顶点重合, , .
15. 如图,将一个三角板 角的顶点与另一个三角板的直角顶点重合, , .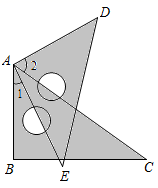 16. 线段 ,在直线 上截取线段 , 为线段 的中点, 为线段 的中点,那么线段 的长为 .
16. 线段 ,在直线 上截取线段 , 为线段 的中点, 为线段 的中点,那么线段 的长为 .三、解答题
-
17. 计算(1)、 ;(2)、 .18. 解方程(1)、 ;(2)、 .19. 先化简,再求值: ,其中 , .20. 某超市计划购进甲、乙两种商品共 件,这两种商品的进价、售价如下表:
进价(元/件)
售价(元/件)
甲
乙
(1)、超市如何进货,进货款恰好为 元?(2)、为确保乙商品畅销,在(1)的条件下,商家决定对乙商品进行打折出售,且全部售完后,乙商品的利润率为 ,请问乙商品需打几折?21. 在如图,所示的方格纸中不用量角器与三角尺,仅用直尺.
( 1 )经过点 画 的平行线 .
( 2 )过点 ,画 的垂线 .
( 3 )过点 ,画 的垂线 .
( 4 )请直接写出 、 的位置关系.
22. 如图①是由一些大小相同的小正方体组合成的简单几何体.(1)、请在图 的方格纸中分别画出它的主视图、左视图和俯视图.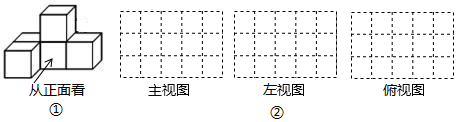 (2)、保持小正方体的个数不变,只改变小正方体的位置,搭一个不同于上图的几何体,使得它的俯视图和左视图与你在方格纸中所画的一致,还有种不同的搭法.23. 已知:如图, 是直线 上一点, 是 的平分线, 与 互余.求证: 与 互补.
(2)、保持小正方体的个数不变,只改变小正方体的位置,搭一个不同于上图的几何体,使得它的俯视图和左视图与你在方格纸中所画的一致,还有种不同的搭法.23. 已知:如图, 是直线 上一点, 是 的平分线, 与 互余.求证: 与 互补.
请将下面的证明过程补充完整;
证明: 是直线 上一点,
与 互余,
_▲_ .
是 的平分线,
_▲_.(理由:_▲_)
.(理由:_▲_)
_▲_ .
与 互补.
24. 2019年9月29日,中国女排以十一连胜的战绩夺得女排世界杯冠军,成为世界三大赛的“十冠王”.2019年女排世界杯的参赛队伍为12支,比赛采取单循环方式,五局三胜,积分规则如下:比赛中以3-0或者3-1取胜的球队积3分,负队积0分;而在比赛中以 取胜的球队积2分,负队积1分,前四名队伍积分榜部分信息如表所示.名次
球队
场次
胜场
负场
总积分
1
中国
11
11
0
________
2
美国
11
10
1
28
3
俄罗斯
11
8
3
23
4
巴西
11
21
(1)、中国队 场胜场中只有一场以 取胜,请将中国队的总积分填在表格中,(2)、巴西队积3分取胜的场次比积2分取胜的场次多5场,且负场积分为1分,总积分见表格,求巴西队胜场的场数.25. 两位同学在用标有数字1,2, ,9的9张卡片做游戏.甲同学:“你先从这9张卡片中随意抽取两张(按抽取的先后顺序分别称为“卡片 ”和“卡片 ”),别告诉我卡片上是什么数字,然后你把卡片 上的数字乘以5,加上7,再乘以2,再加上卡片 上的数字,把最后得到的数 的值告诉我,我就能猜出你抽出的是哪两张卡片啦!”
乙同学:“这么神奇?我不信”……
(1)、【试验】
如果乙同学抽出的卡片 上的数字为2,卡片 上的数字为5,他最后得到的数 ;(2)、若乙同学最后得到的数 ,则卡片 上的数字为 , 卡片 上的数字为 .(3)、【解密】
请你说明:对任意告知的数 ,甲同学是如何猜到卡片的.26. 对于平面内给定射线OA,射线OB及∠MON,给出如下定义:若由射线OA、OB组成的∠AOB的平分线OT落在∠MON的内部或边OM、ON上,则称射线OA与射线OB关于∠MON内含对称.例如,图1中射线OA与射线OB关于∠MON内含对称

已知:如图2,在平面内,∠AOM=10°,∠MON=20°
(1)、若有两条射线 , 的位置如图3所示,且 , ,则在这两条射线中,与射线OA关于∠MON内含对称的射线是(2)、射线OC是平面上绕点O旋转的一条动射线,若射线OA与射线OC关于∠MON内含对称,设∠COM=x°,求x的取值范围;(3)、如图4,∠AOE=∠EOH=2∠FOH=20°,现将射线OH绕点O以每秒1°的速度顺时针旋转,同时将射线OE和OF绕点O都以每秒3°的速度顺时针旋转.设旋转的时间为t秒,且 .若∠FOE的内部及两边至少存在一条以O为顶点的射线与射线OH关于∠MON内含对称,直接写出t的取值范围.