浙江省温州市2021年数学中考模拟试卷(3月)
试卷更新日期:2021-03-22 类型:中考模拟
一、单选题
-
1. 若实数a的相反数是﹣2,则a等于( )A、2 B、﹣2 C、 D、02. 下列把2034000记成科学记数法正确的是( )A、2.034×106 B、20.34×105 C、0.2034×106 D、2.034×1033. 如图所示的几何体,从上面看得到的图形是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 在一只不透明的口袋中放入红球5个,黑球1个,黄球n个,这些球除颜色不同外,其它无任何差别.搅匀后随机从中摸出一个恰好是黄球的概率为 ,则放入口袋中的黄球总数n是( )A、3 B、4 C、5 D、65. 某次校运会共有13名同学报名参加百米赛跑,他们的预赛成绩各不相同,现取其中前6名参加决赛,小勇同学在知道自己成绩的情况下,要判断自己能否进入决赛,还需要知道这13名同学成绩的( )A、平均数 B、众数 C、中位数 D、方差6. 一元一次不等式x+1>2的解在数轴上表示为( )A、
4. 在一只不透明的口袋中放入红球5个,黑球1个,黄球n个,这些球除颜色不同外,其它无任何差别.搅匀后随机从中摸出一个恰好是黄球的概率为 ,则放入口袋中的黄球总数n是( )A、3 B、4 C、5 D、65. 某次校运会共有13名同学报名参加百米赛跑,他们的预赛成绩各不相同,现取其中前6名参加决赛,小勇同学在知道自己成绩的情况下,要判断自己能否进入决赛,还需要知道这13名同学成绩的( )A、平均数 B、众数 C、中位数 D、方差6. 一元一次不等式x+1>2的解在数轴上表示为( )A、 B、
B、 C、
C、 D、
D、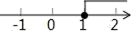 7. 如图,五边形 是 的内接正五边形, 是 的直径,则 的度数是( )
7. 如图,五边形 是 的内接正五边形, 是 的直径,则 的度数是( ) A、18° B、36° C、 D、72°8. 抛物线y=x2﹣2x﹣3与x轴的交点个数是( )A、0个 B、1个 C、2个 D、3个9. 如图,在菱形OABC中,AC=6,OB=8,点O为原点,点B在y轴正半轴上,若函数y= (k≠0)的图象经过点C,则k的值是( )
A、18° B、36° C、 D、72°8. 抛物线y=x2﹣2x﹣3与x轴的交点个数是( )A、0个 B、1个 C、2个 D、3个9. 如图,在菱形OABC中,AC=6,OB=8,点O为原点,点B在y轴正半轴上,若函数y= (k≠0)的图象经过点C,则k的值是( ) A、24 B、12 C、﹣12 D、﹣610. “赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b.若ab=6,大正方形的面积为16,则小正方形的面积为( )
A、24 B、12 C、﹣12 D、﹣610. “赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b.若ab=6,大正方形的面积为16,则小正方形的面积为( ) A、8 B、6 C、4 D、3
A、8 B、6 C、4 D、3二、填空题
-
11. 分解因式:25﹣x2=.12. 已知圆中40°圆心角所对的弧长为3π,则这个圆的周长.13. 某校在全校学生中举办了一次“交通安全知识”测试,张老师从全校学生的答卷中随机地抽取了部分学生的答卷,将测试成绩按“差”、“中”、“良”、“优”划分为四个等级,并绘制成如图所示的条形统计图.若该校学生共有2000人,则其中成绩为“良”和“优”的总人数估计为人.
 14. 如图,△ABC是⊙O的内接三角形,∠A=119°,过点C的圆的切线交BO于点P,则∠P的度数为.
14. 如图,△ABC是⊙O的内接三角形,∠A=119°,过点C的圆的切线交BO于点P,则∠P的度数为. 15. 如图,将边长为9的正方形纸片ABCD沿MN折叠,使点A落在BC边上 点处,点D的对应点为点 ,若 ,则DM=.
15. 如图,将边长为9的正方形纸片ABCD沿MN折叠,使点A落在BC边上 点处,点D的对应点为点 ,若 ,则DM=. 16. 如图是某广场用地板铺设的部分图案,中央是一块正六边形的地板砖,周围是正三角形和正方形的地板砖.从里向外的第1层包括6个正方形和6个正三角形,第2层包括6个正方形和18个正三角形,依此递推,第10层中含有正三角形个数为个.
16. 如图是某广场用地板铺设的部分图案,中央是一块正六边形的地板砖,周围是正三角形和正方形的地板砖.从里向外的第1层包括6个正方形和6个正三角形,第2层包括6个正方形和18个正三角形,依此递推,第10层中含有正三角形个数为个.
三、解答题
-
17.(1)、计算:(﹣2)﹣1+( ﹣1)0﹣|﹣ |;(2)、先化简,再求值: ﹣ ÷ ,其中a=1﹣ .18. 如图,在平行四边形ABCD中,点E为AD的中点,延长CE交BA的延长线于点F.
 (1)、求证:AB=AF;(2)、若BC=2AB,∠BCD=100°,求∠ABE的度数.19. 为了了解学生掌握垃圾分类知识的情况,增强学生环保意识.某校举行了“垃圾分类,人人有责”的知识测试活动,现从该校七、八年级中各随机抽取20名学生的测试成绩(满分10分,6分及6分以上为及格)进行整理、描述和分析,下面给出了部分信息:
(1)、求证:AB=AF;(2)、若BC=2AB,∠BCD=100°,求∠ABE的度数.19. 为了了解学生掌握垃圾分类知识的情况,增强学生环保意识.某校举行了“垃圾分类,人人有责”的知识测试活动,现从该校七、八年级中各随机抽取20名学生的测试成绩(满分10分,6分及6分以上为及格)进行整理、描述和分析,下面给出了部分信息:七年级20名学生的测试成绩为:
7,8,7,9,7,6,5,9,10,9,8,5,8,7,6,7,9,7,10,6
七,八年级抽取的学生的测试成绩的平均数、众数、中位数、8分及以上人数所占百分比如下表所示:
年级
平均数
众数
中位数
8分及以上人数所占百分比
七年级
7.5
a
7
45%
八年级
7.5
8
b
c

根据以上信息,解答下列问题:(1)、在上述表格中:a= , b= , c=;(2)、根据上述数据,你认为该校七、八年级中哪个年级的学生掌握垃圾分类知识的情况较好?请说明理由(写出一条理由即可);(3)、该校德育处从八年级测试成绩前四名甲、乙、丙、丁学生中,随机抽取2名学生参加全市现场垃圾分类知识竞赛,请用列表法或画树状图法求出必有甲同学参加比赛的概率.20. 如图,正方形网格中每个正方形的边长都是1,每个小格的顶点叫做格点,以格点为顶点,分别按下列要求画三角形. (1)、其中一条边为无理数,两条边为有理数;(2)、其中两条边为无理数,一条边为有理数;(3)、三条边都能为无理数吗?若能在图(3)中画出,此三角形的面积是 (填有理数或无理数),并计算出你所画三角形的面积.
(1)、其中一条边为无理数,两条边为有理数;(2)、其中两条边为无理数,一条边为有理数;(3)、三条边都能为无理数吗?若能在图(3)中画出,此三角形的面积是 (填有理数或无理数),并计算出你所画三角形的面积.
21. 如图,△ACE内接于⊙O,AB是⊙O的直径,弦CD⊥AB于点H,交AE于点F,过点E作EG∥AC,分别交CD、AB的延长线于点G、M. (1)、求证:△ECF∽△GCE;(2)、若tanG= ,AH=3 ,求⊙O半径.22. 如图,抛物线 经过点 和 ,与两坐标轴的交点分别为A、B、C,它的对称轴为直线l,顶点为D.
(1)、求证:△ECF∽△GCE;(2)、若tanG= ,AH=3 ,求⊙O半径.22. 如图,抛物线 经过点 和 ,与两坐标轴的交点分别为A、B、C,它的对称轴为直线l,顶点为D.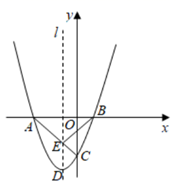 (1)、求该抛物线的表达式和顶点D的坐标;(2)、直线AC交抛物线的对称轴l于点E,在抛物线上是否存在点F,使得△BCF与△BCE的面积相等,如果存在,请求出点F的坐标;如果不存在,请说明理由.23. 甲、乙两个工程队共同承担一项筑路任务,甲队单独施工完成此项任务比乙队单独施工完成此项任务多用 天,且甲队单独施工 天和乙队单独施工 天的工作量相同.(1)、甲、乙两队单独完成此项任务各需多少天?(2)、设先由甲队施工 天,再由乙队施工 天,刚好完成筑路任务,求 与 之间的函数关系式.(3)、在(2)的条件下,若每天需付给甲队的筑路费用为0.1万元,需付给乙队的筑路费用为0.2万元,且甲、乙两队施工的总天数不超过24天,则如何安排甲、乙两队施工的天数,使施工费用最少,并求出最少费用.24. 如图1,△ABC内接于⊙O,∠ACB=60°,D,E分别是 , 的中点,连结DE分别交AC,BC于点F,G.
(1)、求该抛物线的表达式和顶点D的坐标;(2)、直线AC交抛物线的对称轴l于点E,在抛物线上是否存在点F,使得△BCF与△BCE的面积相等,如果存在,请求出点F的坐标;如果不存在,请说明理由.23. 甲、乙两个工程队共同承担一项筑路任务,甲队单独施工完成此项任务比乙队单独施工完成此项任务多用 天,且甲队单独施工 天和乙队单独施工 天的工作量相同.(1)、甲、乙两队单独完成此项任务各需多少天?(2)、设先由甲队施工 天,再由乙队施工 天,刚好完成筑路任务,求 与 之间的函数关系式.(3)、在(2)的条件下,若每天需付给甲队的筑路费用为0.1万元,需付给乙队的筑路费用为0.2万元,且甲、乙两队施工的总天数不超过24天,则如何安排甲、乙两队施工的天数,使施工费用最少,并求出最少费用.24. 如图1,△ABC内接于⊙O,∠ACB=60°,D,E分别是 , 的中点,连结DE分别交AC,BC于点F,G.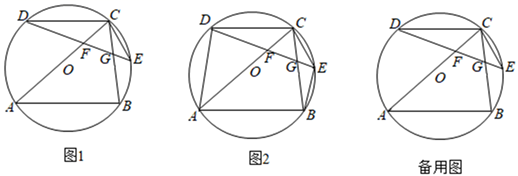 (1)、求证:△DFC∽△CGE;(2)、若DF=3,tan∠GCE= ,求FG的长;(3)、如图2,连结AD,BE,若 =x, =y,求y关于x的函数表达式.
(1)、求证:△DFC∽△CGE;(2)、若DF=3,tan∠GCE= ,求FG的长;(3)、如图2,连结AD,BE,若 =x, =y,求y关于x的函数表达式.