天津市河西区2019-2020学年八年级下学期数学期中试卷
试卷更新日期:2021-03-22 类型:期中考试
一、单选题
-
1. 计算 的结果为( )A、 B、 C、 D、2. 下列图案中,可以看作是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 由下列长度组成的各组线段中,不能组成直角三角形的是( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 下列命题中,真命题是( )A、对角线相等的四边形是矩形 B、对角线互相垂直的四边形是菱形 C、对角线互相平分的四边形是平行四边形 D、对角线互相垂直平分的四边形是正方形6. 如图,点 ,点 ,则AB的长度为( )
3. 由下列长度组成的各组线段中,不能组成直角三角形的是( )A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 下列命题中,真命题是( )A、对角线相等的四边形是矩形 B、对角线互相垂直的四边形是菱形 C、对角线互相平分的四边形是平行四边形 D、对角线互相垂直平分的四边形是正方形6. 如图,点 ,点 ,则AB的长度为( ) A、 B、 C、 D、7. 如图,平行四边形 的对角线 相交于点O,则下列判断错误的是( )
A、 B、 C、 D、7. 如图,平行四边形 的对角线 相交于点O,则下列判断错误的是( )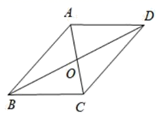 A、 B、 C、 和 的面积相等 D、 和 的面积相等8. 若 为直角三角形的三边,则下列判断错误的是( )A、 能组成直角三角形 B、 能组成直角三角形 C、 能组成直角三角形 D、 能组成直角三角形9. 如图,若将四根木条钉成的矩形木框变形为平行四边形 的形状,并使得其面积变为原矩形面积的一半,则平行四边形 的内角 的大小为( )
A、 B、 C、 和 的面积相等 D、 和 的面积相等8. 若 为直角三角形的三边,则下列判断错误的是( )A、 能组成直角三角形 B、 能组成直角三角形 C、 能组成直角三角形 D、 能组成直角三角形9. 如图,若将四根木条钉成的矩形木框变形为平行四边形 的形状,并使得其面积变为原矩形面积的一半,则平行四边形 的内角 的大小为( ) A、100° B、120° C、135° D、150°10. 如图,在由10个完全相同的正三角形构成的网格图中,连接 .有下列结论:① ;② 是直角三角形;③ .其中,正确结论的个数为( )
A、100° B、120° C、135° D、150°10. 如图,在由10个完全相同的正三角形构成的网格图中,连接 .有下列结论:① ;② 是直角三角形;③ .其中,正确结论的个数为( ) A、0 B、1 C、2 D、3
A、0 B、1 C、2 D、3二、填空题
-
11. 化简 的结果为12. 边长为a的正方形的对角线的长度为 .13. 若平行四边形中两个内角的度数比为1:2,则其中较小的内角为14. 如图,每个小正方形的边长都为1,则 的周长为
 15. 如图,有一四边形空地ABCD,AB⊥AD,AB=3,AD=4,BC=12,CD=13,则四边形ABCD的面积为.
15. 如图,有一四边形空地ABCD,AB⊥AD,AB=3,AD=4,BC=12,CD=13,则四边形ABCD的面积为.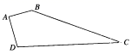 16. 如图, 和 都是等腰直角三角形, , , 的顶点A在 的斜边上.若 , ,则AC的长为
16. 如图, 和 都是等腰直角三角形, , , 的顶点A在 的斜边上.若 , ,则AC的长为
三、解答题
-
17. 计算:(1)、(2)、18. 已知x=2﹣ ,求代数式(7+4 )x2+(2+ )x+ 的值.19. 已知:四边形 , .求证:四边形 是矩形.
 20. 如图,菱形花坛 的一边长 为 , ,沿着该菱形的对角线修建两条小路 和 .
20. 如图,菱形花坛 的一边长 为 , ,沿着该菱形的对角线修建两条小路 和 . (1)、求 和 的长;(2)、求菱形花坛 的面积.21. 如图,在 中, , 于D,M是斜边的中点.
(1)、求 和 的长;(2)、求菱形花坛 的面积.21. 如图,在 中, , 于D,M是斜边的中点. (1)、若 , ,求 的长;(2)、若 ,求 的度数.22. 如图,已知四边形 中, 分别为 上的点(不与端点重合).
(1)、若 , ,求 的长;(2)、若 ,求 的度数.22. 如图,已知四边形 中, 分别为 上的点(不与端点重合). (1)、若 分别为 的中点.求证:四边形 是平行四边形;(2)、在(1)的条件下,根据题意填空:若四边形 的对角线 和 满足时,四边形 是矩形;若四边形 的对角线 和 满足时,四边形 是菱形;若四边形 的对角线 和 满足时,四边形 是正方形.(3)、判断对错:
(1)、若 分别为 的中点.求证:四边形 是平行四边形;(2)、在(1)的条件下,根据题意填空:若四边形 的对角线 和 满足时,四边形 是矩形;若四边形 的对角线 和 满足时,四边形 是菱形;若四边形 的对角线 和 满足时,四边形 是正方形.(3)、判断对错:①若已知的四边形 是任意矩形,则存在无数个四边形 是菱形;( )
②若已知的四边形 是任意矩形,则至少存在一个四边形 是正方形.( )
23. 如图,将一个正方形纸片 放置在平面直角坐标系中,点 , .动点E在边 上,点F在边 上,沿 折叠该纸片,使点O的对应点M始终落在边 上(点M不与A,C重合),点B落在点N处, 与 交于点P. (1)、求点C的坐标;(2)、当点M落在 的中点时,求点E的坐标;(3)、当点M在边 上移动时,设 ,求点E的坐标(用t表示).
(1)、求点C的坐标;(2)、当点M落在 的中点时,求点E的坐标;(3)、当点M在边 上移动时,设 ,求点E的坐标(用t表示).