黄冈市孝感市咸宁市三市2021年数学中考一模联考试卷
试卷更新日期:2021-03-22 类型:中考模拟
一、单选题
-
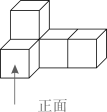
1. 下列各数中,最小的数是( )A、-3 B、0 C、1 D、22. 2020年6月23日9时43分,我国在西昌卫星发射中心用长征三号乙运载火箭,成功发射北斗系统第五十五颗导航卫星,标志着北斗三号卫星导航定位系统正式建成.根据最新数据,目前兼容北斗的终端产品至少有7亿台,其中7亿用科学记数法表示为( )A、 B、 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. 如图是由5个相同的小正方体组成的几何体,该几何题的左视图是( )
 A、
A、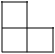 B、
B、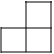 C、
C、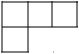 D、
D、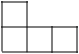 5. 下列说法正确的是( )A、为了解我国中学生课外阅读的情况,应采取全面调查的方式 B、一组数据1、2、5、5、5、3、3的中位数和众数都是5 C、投掷一枚硬币100次,一定有50次“正面朝上” D、若甲组数据的方差是0.03,乙组数据的方差是0.1,则甲组数据比乙组数据稳定6. 如图所示,直线 , , ,则 的度数为( )
5. 下列说法正确的是( )A、为了解我国中学生课外阅读的情况,应采取全面调查的方式 B、一组数据1、2、5、5、5、3、3的中位数和众数都是5 C、投掷一枚硬币100次,一定有50次“正面朝上” D、若甲组数据的方差是0.03,乙组数据的方差是0.1,则甲组数据比乙组数据稳定6. 如图所示,直线 , , ,则 的度数为( )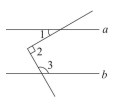 A、120° B、130° C、140° D、150°7. 如图,CD为⊙O的直径,弦AB⊥CD,垂足为M,若AB=12,OM:MD=5:8,则⊙O的周长为( )
A、120° B、130° C、140° D、150°7. 如图,CD为⊙O的直径,弦AB⊥CD,垂足为M,若AB=12,OM:MD=5:8,则⊙O的周长为( ) A、26π B、13π C、 D、8. 如图,在平面直角坐标系中,菱形 在第一象限内,边 与 轴平行, , 两点的纵坐标分别为4,1,反比例函数 的图象经过 , 两点,菱形 的面积为 ,则 的值为( )
A、26π B、13π C、 D、8. 如图,在平面直角坐标系中,菱形 在第一象限内,边 与 轴平行, , 两点的纵坐标分别为4,1,反比例函数 的图象经过 , 两点,菱形 的面积为 ,则 的值为( ) A、4 B、5 C、6 D、9
A、4 B、5 C、6 D、9二、填空题
-
9. 分解因式:9x2﹣6x+1= .10. 为了传承中华民族优秀传统文化,我市某中学举行“经典诵读”比赛,赛后整理参赛学生的成绩,将学生的成绩分为 、 、 、 四个等级,并将结果绘制成如下两幅不完整的统计图.在扇形统计图中, 的值为.

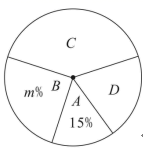 11. 如图,在Rt△ABC中,∠ACB=90°,∠A=50°,以点B为圆心,BC长为半径画弧,交AB于点D,连接CD,则∠ACD的度数是.
11. 如图,在Rt△ABC中,∠ACB=90°,∠A=50°,以点B为圆心,BC长为半径画弧,交AB于点D,连接CD,则∠ACD的度数是. 12. 已知一元二次方程 有两个实数根 , ,则 的值.13. 已知 是不等式组 的整数解,则 的值为.14. 一艘轮船在小岛 的北偏东 方向距小岛 海里的 处,沿正西方向航行 小时后到达小岛的北偏西 的 处,则该船行驶的速度为海里/小时.
12. 已知一元二次方程 有两个实数根 , ,则 的值.13. 已知 是不等式组 的整数解,则 的值为.14. 一艘轮船在小岛 的北偏东 方向距小岛 海里的 处,沿正西方向航行 小时后到达小岛的北偏西 的 处,则该船行驶的速度为海里/小时. 15. 我国古代数学家杨辉发现了如图所示的三角形,我们称之为“杨辉三角”,从图中取一列数:1,3,6,10, ,分别记为 , , , , ,那么 的值是.
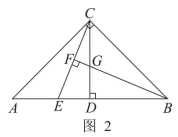
15. 我国古代数学家杨辉发现了如图所示的三角形,我们称之为“杨辉三角”,从图中取一列数:1,3,6,10, ,分别记为 , , , , ,那么 的值是. 16. 如图,先有一张矩形纸片 , , ,点 , 分别在矩形的边 , 上,将矩形纸片沿直线 折叠,使点 落在矩形的边 上,记为点 ,点 落在 处,连接 ,交 于点 ,连接 .下列结论:
16. 如图,先有一张矩形纸片 , , ,点 , 分别在矩形的边 , 上,将矩形纸片沿直线 折叠,使点 落在矩形的边 上,记为点 ,点 落在 处,连接 ,交 于点 ,连接 .下列结论:① ;
②四边形 是菱形;
③ , 重合时, ;
④ 的面积 的取值范围是 .其中正确的;(把正确结论的序号都填上).

三、解答题
-
17. 计算:18. 如图,点M、N分别是正五边形ABCDE的边BC、CD上的点,且BM=CN,AM交BN于点P.
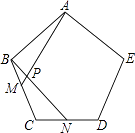 (1)、求证:△ABM≌△BCN;(2)、求∠APN的度数.19. 在一个不透明的口袋里装有红、黄、蓝三种颜色的小球(除颜色外其余都相同),其中红球有2个,蓝球有1个,黄球有1个.(1)、第一次摸出一个球(不放回),第二次再摸一个小球,请用画树状图或列表法求两次摸到都是红球的概率;(2)、若规定摸到红球得5分,摸到黄球得3分,摸到蓝球得1分,小聪共摸6次小球(每次摸1个球,摸后放回)得22分,问小聪有哪几种摸法?20. 如图,在平面直角坐标系中, , 轴于点C,点 在反比例函数 的图象上.
(1)、求证:△ABM≌△BCN;(2)、求∠APN的度数.19. 在一个不透明的口袋里装有红、黄、蓝三种颜色的小球(除颜色外其余都相同),其中红球有2个,蓝球有1个,黄球有1个.(1)、第一次摸出一个球(不放回),第二次再摸一个小球,请用画树状图或列表法求两次摸到都是红球的概率;(2)、若规定摸到红球得5分,摸到黄球得3分,摸到蓝球得1分,小聪共摸6次小球(每次摸1个球,摸后放回)得22分,问小聪有哪几种摸法?20. 如图,在平面直角坐标系中, , 轴于点C,点 在反比例函数 的图象上. (1)、求反比例函数 的解析式;(2)、若在x轴负半轴上存在一点P,使得 ,求点P的坐标.21. 如图, 为 的直径,点 为弦 的中点, 的延长线交 于点 ,连接 , , . 与 交于点 ,点 在 的延长线上,且 .
(1)、求反比例函数 的解析式;(2)、若在x轴负半轴上存在一点P,使得 ,求点P的坐标.21. 如图, 为 的直径,点 为弦 的中点, 的延长线交 于点 ,连接 , , . 与 交于点 ,点 在 的延长线上,且 . (1)、求证: 与 相切;(2)、若 , ,求 的长.22. 某公司分别在 , 两城生产同种产品,共100件. 城生产产品的总成本 (万元)与产品数量 (件)之间具有函数关系 , 城生产产品的每件成本为70万.当 , 两城生产这批产品的总成本的和最少时,求:(1)、 , 两城各生产多少件?(2)、从 城把该产品运往 , 两地的费用分别为 万元/件和3万元/件;从 城把该产品运往 , 两地的费用分别为1万元/件和2万元/件, 地需要90件, 地需要10件,求 , 两城总运费之和 的最小值(用含有 的式子表示).
(1)、求证: 与 相切;(2)、若 , ,求 的长.22. 某公司分别在 , 两城生产同种产品,共100件. 城生产产品的总成本 (万元)与产品数量 (件)之间具有函数关系 , 城生产产品的每件成本为70万.当 , 两城生产这批产品的总成本的和最少时,求:(1)、 , 两城各生产多少件?(2)、从 城把该产品运往 , 两地的费用分别为 万元/件和3万元/件;从 城把该产品运往 , 两地的费用分别为1万元/件和2万元/件, 地需要90件, 地需要10件,求 , 两城总运费之和 的最小值(用含有 的式子表示).