山西省吕梁市兴县2019-2020学年八年级下学期数学期中试卷
试卷更新日期:2021-03-22 类型:期中考试
一、单选题
-
1. 下列根式中,不是最简二次根式的是( )A、 B、 C、 D、2. 计算: ﹣ 的结果是( )A、 B、2 C、 D、23. 如图,正方形ABCD的面积是( )
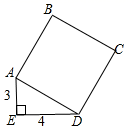 A、5 B、25 C、7 D、14. 如图,菱形 中, ,则 ( )
A、5 B、25 C、7 D、14. 如图,菱形 中, ,则 ( )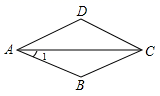 A、 B、 C、 D、5. 在平面直角坐标系中, ▱ABCD的顶点A(0,0),B(5,0),D(2,3),则顶点C的坐标是( )A、(3,7) B、(5,3) C、(7,3) D、(8,2)6. 如图,在△ABC中,D , E分别是AB , AC边的中点,若DE=2,则BC的长度是( )
A、 B、 C、 D、5. 在平面直角坐标系中, ▱ABCD的顶点A(0,0),B(5,0),D(2,3),则顶点C的坐标是( )A、(3,7) B、(5,3) C、(7,3) D、(8,2)6. 如图,在△ABC中,D , E分别是AB , AC边的中点,若DE=2,则BC的长度是( )
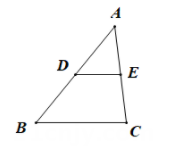 A、6 B、5 C、4 D、37. 下列说法错误的是( )A、平行四边形对边平行 B、两组对边平行的四边形是平行四边形 C、平行四边形对角相等 D、一组对角相等的四边形是平行四边形8. 如图,在平面直角坐标系中,点P坐标为(﹣2,3),以点O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标为( )
A、6 B、5 C、4 D、37. 下列说法错误的是( )A、平行四边形对边平行 B、两组对边平行的四边形是平行四边形 C、平行四边形对角相等 D、一组对角相等的四边形是平行四边形8. 如图,在平面直角坐标系中,点P坐标为(﹣2,3),以点O为圆心,以OP的长为半径画弧,交x轴的负半轴于点A,则点A的横坐标为( ) A、 B、2﹣ C、﹣ D、 ﹣29. 如图,在 中, , , ,D为边 上一动点, 于点E, 于点F,则 的最小值为( )
A、 B、2﹣ C、﹣ D、 ﹣29. 如图,在 中, , , ,D为边 上一动点, 于点E, 于点F,则 的最小值为( ) A、2.4 B、3 C、4.8 D、510. 勾股定理是人类最伟大的科学发现之一,在我国古算书 《周髀算经》 中早有记载。如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )
A、2.4 B、3 C、4.8 D、510. 勾股定理是人类最伟大的科学发现之一,在我国古算书 《周髀算经》 中早有记载。如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出( )
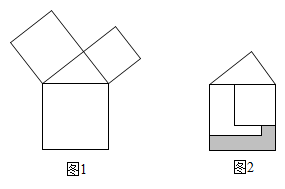 A、直角三角形的面积 B、最大正方形的面积 C、较小两个正方形重叠部分的面积 D、最大正方形与直角三角形的面积和
A、直角三角形的面积 B、最大正方形的面积 C、较小两个正方形重叠部分的面积 D、最大正方形与直角三角形的面积和二、填空题
-
11. 代数式 有意义时,x应满足的条件是 .12. 一个三角形的一边长为 ,这条边上的高为 ,则这个三角形的面积为 .13. 在菱形 中,对角线 、 交于点 ,点 为 中点,过点 作 于点 交 于点 ,连接 ,若 则 °.
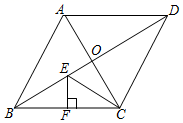 14. 如图,用6个边长为l的小正方形构造的网格图,角 , 的顶点均在格点上,则 .
14. 如图,用6个边长为l的小正方形构造的网格图,角 , 的顶点均在格点上,则 . 15. 如图,在正方形 中, ,点E在正方形 的边上,若 ,则线段 的长为 .
15. 如图,在正方形 中, ,点E在正方形 的边上,若 ,则线段 的长为 .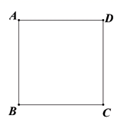
三、解答题
-
16. 计算题.(1)、(2)、17. 为了打赢湖北保卫战、武汉保卫战,4万多名医护人员逆行出征,约4万名建设者从八方赶来,并肩奋战,抢建火神山和雷神山医院.他们日夜鏖战,与病毒竞速,创造了10天左右时间建成两座传染病医院的“中国速度”!他们不畏风险,同困难斗争,充分展现团结起来打硬仗的“中国力量”,在建设过程中,有一位木工遇到了这样一道数学题:
有一块矩形木板,木工采用如图的方式,在木板上截出两个面积分别为 和 的正方形木板.
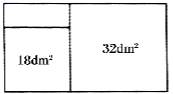 (1)、求剩余木料的面积?(2)、如果木工想从剩余的木料中截出长为 ,宽为 的长方形木条,最多能截出块这样的木条.18. 菱形 中, 于点E,且 , .
(1)、求剩余木料的面积?(2)、如果木工想从剩余的木料中截出长为 ,宽为 的长方形木条,最多能截出块这样的木条.18. 菱形 中, 于点E,且 , . (1)、求 的长;(2)、求菱形 的面积.19. 有一架秋千,当它静止时,踏板离地的垂直高度DE=1m , 将它往前推送6m(水平距离BC=6m)时,秋千的踏板离地的垂直高度BF=4m , 秋千的绳索始终拉得很直,求绳索AD的长度.
(1)、求 的长;(2)、求菱形 的面积.19. 有一架秋千,当它静止时,踏板离地的垂直高度DE=1m , 将它往前推送6m(水平距离BC=6m)时,秋千的踏板离地的垂直高度BF=4m , 秋千的绳索始终拉得很直,求绳索AD的长度. 20.
20. (1)、正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形,在图1正方形网格(每个小正方形边长为1)中画出格点△ABC,使AB=AC=5,BC=(2)、在△ABC中, AB、BC、AC三边的长分别为 、 、 ,求这个三角形的面积.小华同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图2所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.这种方法叫做构图法 .
(1)、正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形,在图1正方形网格(每个小正方形边长为1)中画出格点△ABC,使AB=AC=5,BC=(2)、在△ABC中, AB、BC、AC三边的长分别为 、 、 ,求这个三角形的面积.小华同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图2所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.这种方法叫做构图法 .①△ABC的面积为: .
②若△DEF三边的长分别为 、 、 ,请在图3的正方形网格中画出相应的△DEF , 并利用构图法求出它的面积为 .
21. 已知:如图,平行四边形ABCD中,M、N分别为AB和CD的中点.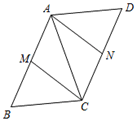 (1)、求证:四边形AMCN是平行四边形;(2)、若AC=BC=5,AB=6,求四边形AMCN的面积.22. 阅读下面材料:
(1)、求证:四边形AMCN是平行四边形;(2)、若AC=BC=5,AB=6,求四边形AMCN的面积.22. 阅读下面材料:在数学课上,老师请同学思考如下问题:如图1,我们把一个四边形ABCD的四边中点E,F,G,H依次连接起来得到的四边形EFGH是平行四边形吗.
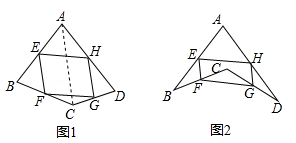
小敏在思考问题时,有如下思路:连接AC.
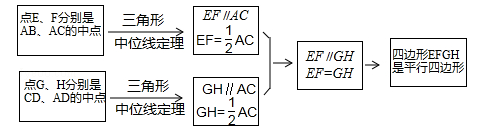
结合小敏的思路作答:
(1)、若只改变图1中四边形ABCD的形状(如图2),则四边形EFGH还是平行四边形吗?说明理由,参考小敏思考问题的方法解决一下问题;(2)、如图2,在(1)的条件下,若连接AC,BD.①当AC与BD满足什么条件时,四边形EFGH是菱形,写出结论并证明;
②当AC与BD满足什么条件时,四边形EFGH是矩形,直接写出结论.
23. 综合与实践:折纸中的数学
问题背景
在数学活动课上,老师首先将平行四边形纸片ABCD按如图①所示方式折叠,使点C与点A重合,点D落到D′处,折痕为EF . 这时同学们很快证得:△AEF是等腰三角形.接下来各学习小组也动手操作起来,请你解决他们提出的问题.
操作发现
(1)、“争先”小组将矩形纸片ABCD按上述方式折叠,如图②,发现重叠部分△AEF恰好是等边三角形,求矩形ABCD的长、宽之比是多少?(2)、实践探究“励志”小组将矩形纸片ABCD沿EF折叠,如图③,使B点落在AD边上的B′处;沿B′G折叠,使D点落在D′处,且B′D′过F点.试探究四边形EFGB′是什么特殊四边形?
(3)、再探究:在图③中连接BB′,试判断并证明△BB′G的形状.