山西省吕梁市交城县2019-2020学年八年级下学期数学期中试卷
试卷更新日期:2021-03-22 类型:期中考试
一、单选题
-
1. 若代数式 有意义,则x的取值范围是( )A、 B、 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 我国数学家华罗庚曾建议,用一副反应勾股定理的数形关系图来作为和外星人交谈的语言,就勾股定理本身而言,它揭示了直角三角形的三边之间的关系,它体现的数学思想方法是( )A、分类思想 B、方程思想 C、转化 D、数形结合4. 如图,在平行四边形 中,对角线 与 相交于点O,E是边 的中点,连接 .若∠ADC=∠EOC=45°,则 的度数为( )
 A、30° B、45° C、60° D、90°5. 如图,在数轴上点B,点C表示的数分别为4,1, AC⊥BC,AC=1,以B点为圆心, 长为半径画弧,交数轴于点D,则D点表示的数是( )
A、30° B、45° C、60° D、90°5. 如图,在数轴上点B,点C表示的数分别为4,1, AC⊥BC,AC=1,以B点为圆心, 长为半径画弧,交数轴于点D,则D点表示的数是( ) A、 B、 C、 D、6. 如图,平行四边形 中,对角线 与 相交于点 , 、 分别是对角线BD上的两点,给出下列四个条件:① ;② ;③ ;④ .其中能判断四边形 是平行四边形的个数是( )
A、 B、 C、 D、6. 如图,平行四边形 中,对角线 与 相交于点 , 、 分别是对角线BD上的两点,给出下列四个条件:① ;② ;③ ;④ .其中能判断四边形 是平行四边形的个数是( )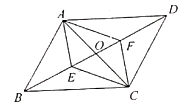 A、1个 B、2个 C、3个 D、4个7. 数学课上,老师要同学们判断一个四边形门框是否为矩形.下面是某合作小组4位同学拟定的方案,其中正确的是( )A、测量对角线是否互相平分 B、测量两组对边是否分别相等 C、测量一组对角是否都为直角 D、测量三个角是否为直角8. 设 =a, =b,用含a,b的式子表示 ,则下列表示正确的是( )A、0.3ab B、3ab C、0.1ab2 D、0.1a2b9. 如图,菱形 中, , .点 、 分别为 、 的中点,连接 、 、EF , 则 的周长为( )
A、1个 B、2个 C、3个 D、4个7. 数学课上,老师要同学们判断一个四边形门框是否为矩形.下面是某合作小组4位同学拟定的方案,其中正确的是( )A、测量对角线是否互相平分 B、测量两组对边是否分别相等 C、测量一组对角是否都为直角 D、测量三个角是否为直角8. 设 =a, =b,用含a,b的式子表示 ,则下列表示正确的是( )A、0.3ab B、3ab C、0.1ab2 D、0.1a2b9. 如图,菱形 中, , .点 、 分别为 、 的中点,连接 、 、EF , 则 的周长为( )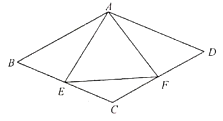 A、9 B、 C、 D、10. 如图,依次连接边长为1的小正方形各边的中点,得到第二个小正方形,再依次连接第二个小正方形各边的中点得到第三个小正方形,按这样的规律第2019个小正方形的面积为( )
A、9 B、 C、 D、10. 如图,依次连接边长为1的小正方形各边的中点,得到第二个小正方形,再依次连接第二个小正方形各边的中点得到第三个小正方形,按这样的规律第2019个小正方形的面积为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若 ,则 .12. 我国南宋著名数学家秦九少韶的著作《数书九章》记载有这样一道题:“问有沙田一块,有三斜,其中小斜三里,中斜四里,大斜五里,欲知为田几何?”这道题讲的是有一块三角形沙田,三条边长分别为3里,4里,5里,问这块沙田的面积有多大?题中“里”是我国市制单位,1里=500米,则沙田的面积为平方千米.13.
如图所示,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为
 14. 如图,数轴上 点表示的数是 ,化简 .
14. 如图,数轴上 点表示的数是 ,化简 .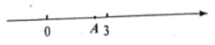 15. 数学课上,小明给出了画菱形的一种方法,如图,分别以点 , 为圆心,大于 长为半径画弧,两弧相交于 、 两点,分别连接 、 、 、 ,所得四边形 为菱形,这样做的依据是.
15. 数学课上,小明给出了画菱形的一种方法,如图,分别以点 , 为圆心,大于 长为半径画弧,两弧相交于 、 两点,分别连接 、 、 、 ,所得四边形 为菱形,这样做的依据是.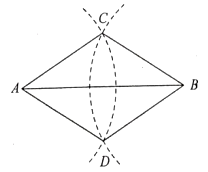 16. 如图,四边形 是正方形, ,点 是对角线 的中点,将 绕点 旋转,其中 ,两直角边 、 分别与边 、 相交于点 、 ,连接 .在旋转过程中 的最小值为.
16. 如图,四边形 是正方形, ,点 是对角线 的中点,将 绕点 旋转,其中 ,两直角边 、 分别与边 、 相交于点 、 ,连接 .在旋转过程中 的最小值为.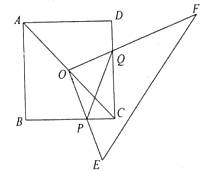
三、解答题
-
17. 计算:(1)、(2)、已知 , ,.求: 的值.18. 三边长分别为 、 、 ,求这个三角形的面积,小明同学在求面积时先画了一个每个小正方形的边长均为1的正方形网格,再在网格中画出格点 ( 各个顶点都在网格的格点上).如图1所示,这样借用网格(不需 的高)就能算出三角形的面积,这种方法叫构造法.
 (1)、 的面积为.(2)、若 的三边长分别为 、 、 ,请在图2的网格中画出 ,使得 的三个顶点都在格点上,求此三角形的面积.19. 如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)、 的面积为.(2)、若 的三边长分别为 、 、 ,请在图2的网格中画出 ,使得 的三个顶点都在格点上,求此三角形的面积.19. 如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
求证:四边形AEBD是矩形.
20. 已知 中, ,点 是斜边 上的中点,过点 作 边上的垂线 ,垂足为点 ,连接 ,过点 作 与 的延长线相交于点 .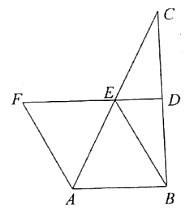 (1)、找出图中与 相等的所有线段.(2)、若 , ,求四边形 的面积.21. 如图,为了修建某条高速铁路需凿通隧道AC,现量出∠A+∠B=∠C,AB=10km,BC=6km,若每天开凿隧道0.4km,问多少天才能把隧道AC凿通?
(1)、找出图中与 相等的所有线段.(2)、若 , ,求四边形 的面积.21. 如图,为了修建某条高速铁路需凿通隧道AC,现量出∠A+∠B=∠C,AB=10km,BC=6km,若每天开凿隧道0.4km,问多少天才能把隧道AC凿通? 22. 观察下列式子变形过程,完成下列任务:(1)、类比上述变形过程的基本思路,猜想 的结果并验证;(2)、算: .23. 综合与实践
22. 观察下列式子变形过程,完成下列任务:(1)、类比上述变形过程的基本思路,猜想 的结果并验证;(2)、算: .23. 综合与实践数学活动课上,小红画了如图1所示的两个共用直角顶点的等腰直角三角形 与等腰直角三角形 ,其中 , ,连接 , 、 、 分别为边 、 、 的中点,连接 、 .
 (1)、操作发现:
(1)、操作发现:小红发现了: 、 有一定的关系,数量关系为;位置关系为.
(2)、类比思考:如图2,在图1的基础上,将等腰直角三角形 绕点 旋转一定的角度,其它条件都不变,小红发现的结论还成立吗?请说明理由.(提示:连接 、 并延长交于一点 )
深入探究:
在上述类比思考的基础上,小红做了进一步的探究.如图3,作任意一个三角形 ,其中 ,在三角形外侧以 为腰作等腰直角三角形 ,以 为腰作等腰直角三角形 ,分别取斜边 、 与边 的中点 、 、 ,连接 、 、 ,试判断三角形 的形状,并说明理由.
