山西省晋中市寿阳县2019-2020学年八年级下学期数学期中试卷
试卷更新日期:2021-03-22 类型:期中考试
一、单选题
-
1. 随着人们生活水平的提高,我国拥有汽车的居民家庭也越来越多,下列汽车标志中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列变形错误的是( )A、若a>b , 则b<a B、若-a>-b , 则b>a C、由-2x>a , 得x>- a D、由 x>-y , 得x>-2y3. 不等式组 的解集在数轴上表示正确的是( )A、
2. 下列变形错误的是( )A、若a>b , 则b<a B、若-a>-b , 则b>a C、由-2x>a , 得x>- a D、由 x>-y , 得x>-2y3. 不等式组 的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、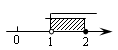 D、
D、 4. 下列判断中错误的是( )A、有两角和一边对应相等的两个三角形全等 B、有两边和一角对应相等的两个三角形全等 C、有两边和其中一边上的中线对应相等的两个三角形全等 D、有一边对应相等的两个等边三角形全等5. 若不等式 的解集是 ,则a必满足 ( )A、 B、 C、 D、6. 如图(1)中,△ABC和△ADE都是等腰直角三角形,∠ACB和∠D都是直角,点C在AE上,△ABC绕着A点经过逆时针旋转后能够与△ADE重合,再将图(1)作为“基本图形”绕着A点经过逆时针旋转得到图(2).两次旋转的角度分别为( )
4. 下列判断中错误的是( )A、有两角和一边对应相等的两个三角形全等 B、有两边和一角对应相等的两个三角形全等 C、有两边和其中一边上的中线对应相等的两个三角形全等 D、有一边对应相等的两个等边三角形全等5. 若不等式 的解集是 ,则a必满足 ( )A、 B、 C、 D、6. 如图(1)中,△ABC和△ADE都是等腰直角三角形,∠ACB和∠D都是直角,点C在AE上,△ABC绕着A点经过逆时针旋转后能够与△ADE重合,再将图(1)作为“基本图形”绕着A点经过逆时针旋转得到图(2).两次旋转的角度分别为( ) A、45°,90° B、90°,45° C、60°,30° D、30°,60°7. 如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
A、45°,90° B、90°,45° C、60°,30° D、30°,60°7. 如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )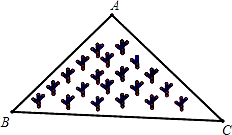 A、△ABC的三条中线的交点 B、△ABC三边的中垂线的交点 C、△ABC三条角平分线的交点 D、△ABC三条高所在直线的交点8. 如图,在△ABC中,∠A=36°,AB=AC,BD是△ABC的角平分线.若在边AB上截取BE=BC,连接DE,则图中等腰三角形共有( )
A、△ABC的三条中线的交点 B、△ABC三边的中垂线的交点 C、△ABC三条角平分线的交点 D、△ABC三条高所在直线的交点8. 如图,在△ABC中,∠A=36°,AB=AC,BD是△ABC的角平分线.若在边AB上截取BE=BC,连接DE,则图中等腰三角形共有( )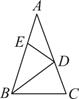 A、2个 B、3个 C、4个 D、5个9.
A、2个 B、3个 C、4个 D、5个9.已知,如图,在△ABC中,OB和OC分别平分∠ABC和∠ACB,过O作DE∥BC,分别交AB、AC于点D、E,若BD+CE=5,则线段DE的长为( )
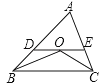 A、5 B、6 C、7 D、810. 轮船从B处以每小时50海里的速度沿南偏东30°方向匀速航行,在B处观测灯塔A位于南偏东75°方向上,轮船航行半小时到达C处,在C处观测灯塔A位于北偏东60°方向上,则C处与灯塔A的距离是( )海里.
A、5 B、6 C、7 D、810. 轮船从B处以每小时50海里的速度沿南偏东30°方向匀速航行,在B处观测灯塔A位于南偏东75°方向上,轮船航行半小时到达C处,在C处观测灯塔A位于北偏东60°方向上,则C处与灯塔A的距离是( )海里. A、50 B、25 C、25 D、25
A、50 B、25 C、25 D、25二、填空题
-
11. 等腰三角形中一个角为40°,则它的底角的度数为 .12. 如图,将一幅三角尺如图所示叠放在一起,若AB=24cm,则阴影部分的面积是 .
 13. 如图所示,在△ABC中,∠B=90°,AB=3,AC=5,将△ABC折叠,使点C与点A重合,折痕为DE,则△ABE的周长为.
13. 如图所示,在△ABC中,∠B=90°,AB=3,AC=5,将△ABC折叠,使点C与点A重合,折痕为DE,则△ABE的周长为.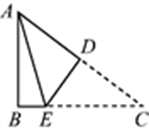 14. 如果关于x的不等式组 无解,则a的取值范围是.15. 如图,已知AB=A1B,A1C=A1A2 , A2D=A2A3 , A3E=A3A4 , …,以此类推,若∠B=20°,则∠A4= .
14. 如果关于x的不等式组 无解,则a的取值范围是.15. 如图,已知AB=A1B,A1C=A1A2 , A2D=A2A3 , A3E=A3A4 , …,以此类推,若∠B=20°,则∠A4= . 16. 已知 是等边三角形,点D、E分别在AC、BC上,且 ,则 .
16. 已知 是等边三角形,点D、E分别在AC、BC上,且 ,则 .
三、解答题
-
17. 解不等式(组),并将解集表示在数轴上:(1)、解不等式(2)、解不等式组:18. 在数学学习中,及时对知识进行归纳和整理是改善学习的重要方法.善于学习的小明在学习了一次方程(组).一元一次不等式和一次函数后,对相关知识进行了归纳整理.

 (1)、例如,他在同一个直角坐标系中画出了一次函数y=x+2和y=-x+4的图像(如图1),并作了归纳:
(1)、例如,他在同一个直角坐标系中画出了一次函数y=x+2和y=-x+4的图像(如图1),并作了归纳:
请根据图1和以上方框中的内容,在下面数字序号后写出相应的结论:
① ;②;
③;④;
(2)、若已知一次函数y=k1x+b1和y=kx+b的图像(如图2),且它们的交点C的坐标为(1,3),那么不等式kx+b≥k1x+b1的解集 .19. 如图,CE⊥AB,BF⊥AC,垂足为E,F,CE与BF相交于D,且AE=AF.求证:DE=DF 20. 若不等式 的正整数解是方程 的解,求 的值.21. 在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4)
20. 若不等式 的正整数解是方程 的解,求 的值.21. 在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4)
⑴画出△ABC先向左平移1个单位,再向下平移4个单位得到的△A1B1C1 , 写出点A1的坐标
⑵画出△A1B1C1绕原点O顺时针旋转90°,得到△A2B2C2 , 写出点A2的坐标
22. 某校长暑假将带领该校市级“三好学生”去北京旅游,甲旅行社说:“如果校长买全票一张,则其余的学生可享受半价优惠.”乙旅行社说:“包括校长在内全部按票价的六折优惠.”若全票价为240元,两家旅行社的服务质量相同,根据“三好学生”的人数你认为选择哪一家旅行社才比较合算?23. 如图,在△ABC和△ADE中,点E在BC边上,∠B=∠D,AB=AD,∠BAD=∠CAE, (1)、求证:AE=AC(2)、若∠AEC=60°,将△ADE绕点A逆时针旋转后与△ABC重合,则这个旋转角的度数(3)、若AC=4,BC=7,∠AEC=60°,求△ABE的面积.24.
(1)、求证:AE=AC(2)、若∠AEC=60°,将△ADE绕点A逆时针旋转后与△ABC重合,则这个旋转角的度数(3)、若AC=4,BC=7,∠AEC=60°,求△ABE的面积.24. (1)、问题情境,如图1,△ABC的边BC在直线m上,AC⊥BC,且AC=BC,△EFP的边FP也在直线m上,边EF与边AC重合,且EF=FP,
(1)、问题情境,如图1,△ABC的边BC在直线m上,AC⊥BC,且AC=BC,△EFP的边FP也在直线m上,边EF与边AC重合,且EF=FP,在图1中,AB与AP的数量关系是 , AB与AP的位置关系是
(2)、操作发现:将△EFP沿直线m向左平移到图2的位置时,EP交AC于点Q,连接AP,BQ,猜想并证明BQ与AP的数量关系和位置关系(3)、猜想论证:将△EFP沿直线m向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连接AP,BQ,(2)中的结论还成立吗?为什么?