内蒙古巴彦淖尔市杭锦后旗2019-2020学年八年级下学期数学期中试卷
试卷更新日期:2021-03-22 类型:期中考试
一、单选题
-
1. 下列根式中属最简二次根式的是( )A、 B、 C、 D、2. 下列计算正确的是( )A、5 -2 =3 B、2 ×3 =6 C、 +2 =3 D、3 ÷ =33. 下列各式中,一定能成立的是( )A、 B、 C、 =x-1 D、4. 如图,“赵爽弦图”是由四个全等的直角三角形拼成一个大的正方形,是我国古代数学的骄傲,巧妙地利用面积关系证明了勾股定理. 已知小正方形的面积是1,直角三角形的两直角边分别为a、b且ab=6,则图中大正方形的边长为( )
 A、5 B、 C、4 D、35. 一位工人师傅测量一个等腰三角形工件的腰,底及底边上的高,并按顺序记录下数据,量完后,不小心与其他记录的数据记混了,请你帮助这位师傅从下列数据中找出等腰三角形工件的数据( )A、13,10,10 B、13,10,12 C、13,12,12 D、13,10,116.
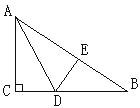
A、5 B、 C、4 D、35. 一位工人师傅测量一个等腰三角形工件的腰,底及底边上的高,并按顺序记录下数据,量完后,不小心与其他记录的数据记混了,请你帮助这位师傅从下列数据中找出等腰三角形工件的数据( )A、13,10,10 B、13,10,12 C、13,12,12 D、13,10,116.如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm.现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )
 A、2cm B、3cm C、4cm D、5cm7. 如图,在 中,AB=AC=8,∠BAC=60°,E是高AD上的一个动点,F是边AB的中点,则 的最小值是( )
A、2cm B、3cm C、4cm D、5cm7. 如图,在 中,AB=AC=8,∠BAC=60°,E是高AD上的一个动点,F是边AB的中点,则 的最小值是( ) A、4 B、4 C、8 D、88. 在四边形ABCD中,若有下列四个条件:①AB//CD;②AD=BC;③∠A=∠C;④AB=CD,现以其中的两个条件为一组,能判定四边形ABCD是平行四边形的条件有( )A、3组 B、4组 C、5组 D、6组9. 如图,在菱形ABCD中,AB=5,对角线AC=6.若过点A作AE⊥BC,垂足为E,则AE的长为( )
A、4 B、4 C、8 D、88. 在四边形ABCD中,若有下列四个条件:①AB//CD;②AD=BC;③∠A=∠C;④AB=CD,现以其中的两个条件为一组,能判定四边形ABCD是平行四边形的条件有( )A、3组 B、4组 C、5组 D、6组9. 如图,在菱形ABCD中,AB=5,对角线AC=6.若过点A作AE⊥BC,垂足为E,则AE的长为( ) A、4 B、2.4 C、4.8 D、510. 如图,已知四边形ABCD是平行四边形,下列结论中错误的是()
A、4 B、2.4 C、4.8 D、510. 如图,已知四边形ABCD是平行四边形,下列结论中错误的是()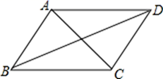 A、当AB=BC时,它是菱形 B、当AC⊥BD时,它是菱形 C、当∠ABC=90°时,它是矩形 D、当AC=BD时,它是正方形11. 四边形ABCD为平行四边形,延长AD到点E , 使DE=AD , 连接EB , EC , DB . 添加一个条件,不能使四边形DBCE成为矩形的是( )
A、当AB=BC时,它是菱形 B、当AC⊥BD时,它是菱形 C、当∠ABC=90°时,它是矩形 D、当AC=BD时,它是正方形11. 四边形ABCD为平行四边形,延长AD到点E , 使DE=AD , 连接EB , EC , DB . 添加一个条件,不能使四边形DBCE成为矩形的是( ) A、DB=DE B、AB=BE C、∠ADB=90° D、CE⊥DE12. 如图,△ABC中,AB=AC,点D、E分别是边AB、AC的中点,点G、F在BC边上,四边形DEFG是正方形.若DE=2cm,则AC的长为( )
A、DB=DE B、AB=BE C、∠ADB=90° D、CE⊥DE12. 如图,△ABC中,AB=AC,点D、E分别是边AB、AC的中点,点G、F在BC边上,四边形DEFG是正方形.若DE=2cm,则AC的长为( )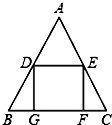 A、 cm B、4cm C、 cm D、2 cm
A、 cm B、4cm C、 cm D、2 cm二、填空题
-
13. 计算: = .14. 要使式子 有意义,则x的取值范围为 .15. 若一个三角形的一边长为a , 这条边上的高为6 ,其面积与一个边长为3 的正方形的面积相等,则a= .16. 在平行四边形ABCD中,M为AD的中点,BM平分∠ABC,如果∠A=120°,MC=3,则△BMC的面积 .17. 矩形的一边长是3.6㎝, 两条对角线的夹角为60º,则矩形对角线长是.18. 如图,▱ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=24厘米,△OAB的周长是18厘米,则EF=厘米.
 19. 如图,在▱ABCD中,用直尺和圆规作∠BAD的平分线AG,若AD=5,DE=6,则AG的长是 .
19. 如图,在▱ABCD中,用直尺和圆规作∠BAD的平分线AG,若AD=5,DE=6,则AG的长是 .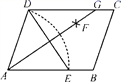 20.
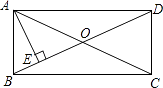
20.如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE⊥BD,垂足为点E,若∠EAC=2∠CAD,则∠BAE=度.
三、解答题
-
21.(1)、计算:(2)、已知x= +1,求x+1- 的值;22. 如图,A城气象台测得台风中心在A城正西方向320km的B处,以每小时40km的速度向北偏东60˚的BF方向移动,距离台风中心200km的范围内是受台风影响的区域.
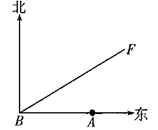 (1)、A城是否受到这次台风的影响?为什么?(2)、若A城受到这次台风影响,则A城遭受这次台风影响有多长时间?23.
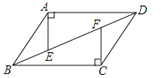
(1)、A城是否受到这次台风的影响?为什么?(2)、若A城受到这次台风影响,则A城遭受这次台风影响有多长时间?23.如图,四边形ABCD中,AD∥BC,AE⊥AD交BD于点E,CF⊥BC交BD于点F,且AE=CF.求证:四边形ABCD是平行四边形.
 24. 将矩形ABCD折叠使A,C重合,折痕交BC于E,交AD于F,
24. 将矩形ABCD折叠使A,C重合,折痕交BC于E,交AD于F, (1)、求证:四边形AECF为菱形;(2)、若AB=4,BC=8,求菱形的边长.25. 如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连结BF.
(1)、求证:四边形AECF为菱形;(2)、若AB=4,BC=8,求菱形的边长.25. 如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连结BF. (1)、线段BD与CD有何数量关系,为什么?(2)、当△ABC满足什么条件时,四边形AFBD是矩形?请说明理由.(3)、当△ABC满足什么条件时,四边形AFBD是正方形?请说明理由.26. 如图,点P是正方形ABCD内的一点,连接CP,将线段CP绕点C顺时针旋转90°,得到线段CQ,连接BP,DQ.
(1)、线段BD与CD有何数量关系,为什么?(2)、当△ABC满足什么条件时,四边形AFBD是矩形?请说明理由.(3)、当△ABC满足什么条件时,四边形AFBD是正方形?请说明理由.26. 如图,点P是正方形ABCD内的一点,连接CP,将线段CP绕点C顺时针旋转90°,得到线段CQ,连接BP,DQ.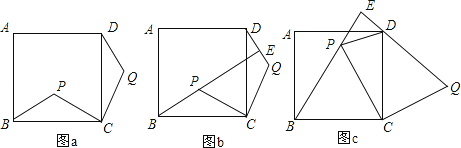 (1)、如图a,求证:△BCP≌△DCQ;(2)、如图,延长BP交直线DQ于点E.
(1)、如图a,求证:△BCP≌△DCQ;(2)、如图,延长BP交直线DQ于点E.①如图b,求证:BE⊥DQ;
②如图c,若△BCP为等边三角形,判断△DEP的形状,并说明理由.