陕西省宝鸡市陇县2020-2021学年八年级上学期数学期末考试试卷

试卷更新日期：2021-03-22 类型：期末考试

进入出卷网下载

一、单选题

1. 若分式 $\frac{x}{x - 2}$ 有意义，则x应满足的条件是（）

A、 $x \neq 2$ B、 $x = 2$ C、 $x > 2$ D、 $x \neq 0$

查看试题解析
2. 在三角形ABC中，AB=7，BC=2，并且AC的长为奇数，则AC=（）

A、3 B、5 C、7 D、9

查看试题解析
3. 芯片是手机、电脑等高科技产品的核心部件，目前我国芯片已可采用14纳米工艺。已知14纳米为0. 0000000 14米，数据0. 0000000 14用科学记数法表示为（）

A、 $1.4 \times 10^{- 10}$ B、 $1.4 \times 10^{- 8}$ C、 $14 \times 10^{- 8}$ D、 $1.4 \times 10^{- 9}$

查看试题解析
4. 如图，△ABC中，BD平分∠ABC，EF垂直平分BC交BC于点E，交BD于点F，连接CF，若∠A=60°，∠ABD=25°，则∠ACF的度数为（）

A、25° B、45° C、50° D、70°

查看试题解析
5. 下列运算正确的是（）

A、a²•b³=a⁶ B、（a²）⁵=a⁷ C、（﹣3b）²=6b² D、a³÷a²=a

查看试题解析
6. 如图，在 $△ A B C$ 中， $∠ C = 90^{\circ}$ ，点 $E$ 是 $A C$ 上的点，且 $∠ 1 = ∠ 2 ， D E$ 垂直平分 $A B$ ，垂足是 $D$ .如果 $E C = 4 c m$ ，则 $A E$ 等于（）

A、 $10 c m$ B、 $8 c m$ C、 $6 c m$ D、 $5 c m$

查看试题解析
7. 若 $a^{2}$ +(m－3)a+4是一个完全平方式，则m的值应是（）

A、1或5 B、1 C、7或－1 D、－1

查看试题解析
8. 如图，已知△ABC中，∠ABC=45°，F是高AD和BE的交点，CD=4，则线段DF的长度为（）

A、 $2 \sqrt{2}$ B、4 C、 $3 \sqrt{2}$ D、 $4 \sqrt{2}$

查看试题解析
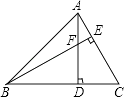9. 已知关于x的分式方程 $\frac{x}{x - 2} - 4 = \frac{k}{2 - x}$ 的解为正数，则k的取值范围是（）

A、 $- 8 < k < 0$ B、 $k > - 8$ 且 $k \neq - 2$ C、 $k > - 8$ 且 $k \neq 2$ D、 $k < 4$ 且 $k \neq - 2$

查看试题解析
10. 如图，AB⊥CD，且AB＝CD.E、F是AD上两点，CE⊥AD，BF⊥AD，若CE＝6，BF＝3，EF＝2，则AD的长为（）

A、7 B、6 C、5 D、4

查看试题解析

二、填空题

11. 计算： ${(- \frac{1}{3})}^{- 2}$ =.

查看试题解析
12. 如图，在正五边形ABCDE中，DM是边CD的延长线，连接BD，则∠BDM的度数是.

查看试题解析
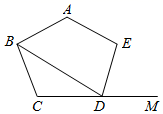13. 若2ⁿ+2ⁿ+2ⁿ+2ⁿ=2⁸ ，则n=.

查看试题解析
14. 如图，在△ABC中，AB=AC，D、E是△ABC内两点，AD平分∠BAC，∠EBC=∠E=60°，若BE=6cm，DE=2cm，则BC=cm．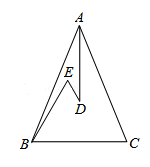

查看试题解析

三、解答题

15. 分解因式：

(1)、3ax²﹣6axy+3ay²；

(2)、（x+1）²﹣2（x+5）.

查看试题解析
16. 化简下列各式：

(1)、 ${(2 x + y)}^{2} - (- x + y) (x + y) - (2 x + y) (x - 2 y)$ ；

(2)、 $(a - 1 + \frac{1}{a + 1}) \div \frac{a^{2} + 2 a}{a + 1}$ .

查看试题解析
17. 已知：∠α，直线l及l上两点A，B.求作：Rt△ABC，使点C在直线l的上方，且∠ABC＝90°，∠BAC＝∠α.

查看试题解析
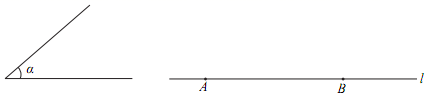18. 如图，点E，F在BC上，BE＝CF，∠A＝∠D，∠B＝∠C，AF与DE交于点O.

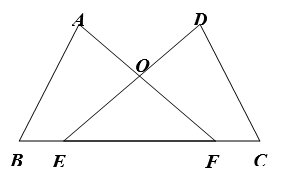(1)、求证：AB＝DC；

(2)、试判断△OEF的形状，并说明理由.

查看试题解析
19. 先化简，再求值： $(\frac{1}{x - 1} - \frac{1}{x + 1}) \div \frac{x + 2}{x^{2} - 1}$ ，然后从-1，0，1中选择适当的数代入求值．

查看试题解析
20. 解方程：

(1)、 $\frac{x - 8}{x - 7} - \frac{1}{7 - x} = 8$ ；

(2)、 $\frac{x}{x - 2} - \frac{1}{x^{2} - 4} = 1$ .

查看试题解析
21. 如图，△ABC中，AB=AC，点E，F在边BC上，AE=AF，点D在AF的延长线上，AD=AC.

(1)、求证：△ABE≌△ACF；

(2)、若∠BAE=30°，求∠ADC的度数.

查看试题解析
22. 为了响应打赢“蓝天保卫战”的号召，张老师上下班的交通方式由驾车改为骑自行车，张老师的家距学校的路程是8千米；在相同的路线上，驾车的平均速度是骑自行车平均速度的3倍，这样，张老师每天上班要比开车早出发 $\frac{1}{3}$ 小时，才能按原驾车时间到达学校.

(1)、求张老师骑自行车的平均速度；

(2)、据测算，张老师的汽车在上下班行驶过程中平均每小时碳排放量约为12千克，这样张老师一天（按一个往返计算）可以减少碳排放量多少千克.

查看试题解析