河北省唐山市古冶区2019-2020学年八年级下学期数学期中试卷

试卷更新日期：2021-03-22 类型：期中考试

进入出卷网下载

一、单选题

1. 如果三条线段的长a，b，c满足a²＝c²－b² ，则这三条线段组成的三角形是（）

A、锐角三角形 B、直角三角形 C、钝角三角形 D、无法确定

查看试题解析
2. 正比例函数y＝2x的比例系数是（　　）

A、1 B、2 C、x D、2x

查看试题解析
3. 一次函数y=﹣2x+1的图象不经过（　　）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 下列二次根式不是最简二次根式的是（　　）

A、 $\sqrt{2}$ B、 $\sqrt{3}$ C、 $\sqrt{7}$ D、 $\sqrt{18}$

查看试题解析
5. 下列各组数据中能作为直角三角形的三边长的是（　　）

A、1，1， $\sqrt{3}$ B、6，8，11 C、3，4，5 D、1，3， $\sqrt{5}$

查看试题解析
6. 如图，在▱ABCD中，AD＝6cm ， AB＝4cm ，则▱ABCD的周长是（　　）

A、12cm B、20cm C、16cm D、24cm

查看试题解析
7. 下列关于正比例函数 $y = - 5 x$ 的说法中，正确的是（）．

A、当 $x = 1$ 时， $y = 5$ B、它的图象是一条经过原点的直线 C、y随x的增大而增大 D、它的图象经过第一、三象限

查看试题解析
8. 已知一次函数 $y = k x + b$ 的图象如图所示，则 $k$ ， $b$ 的符号是（）

A、 $k > 0$ ， $b > 0$ B、 $k > 0$ ， $b < 0$ C、 $k < 0$ ， $b > 0$ D、 $k < 0$ ， $b < 0$

查看试题解析
9. 如图，在直角坐标系中，有两点 $(2 ， 0)$ 和 $(0 ， 3)$ ，则这两点之间的距离是（）

A、 $\sqrt{13}$ B、13 C、 $\sqrt{5}$ D、5

查看试题解析
10. 下列命题中，真命题是（　　）

A、对角线互相平分的四边形是平行四边形 B、对角线互相垂直的四边形是矩形 C、对角线相等的四边形是菱形 D、四个角相等的四边形是正方形

查看试题解析
11. 如图，把正方形纸片ABCD沿对边中点所在的直线对折后展开，折痕为MN，再过点B折叠纸片，使点A落在MN上的点F处，折痕为BE，若AB的长为2，则FM的长为（）

A、2 B、 C、 D、1

查看试题解析
12. 如图，菱形ABCD的周长为8cm，高AE长为 $\sqrt{3}$ cm，则对角线AC长和BD长之比为（）

A、1：2 B、1：3 C、1： D、1：

查看试题解析

二、填空题

13. 在▱ABCD中，若∠A=40°，则∠C=°.

查看试题解析
14. 直线y＝2x+3与y轴的交点坐标是．

查看试题解析
15. 一个矩形的抽斗长为12cm，宽为5cm，在抽斗底部放一根铁条，那么铁条最长可以是cm．

查看试题解析
16. 如图，将▱ABCD中，AD＝8，点E ， F分别是BD ， CD的中点，则EF为．

查看试题解析
17. 如图，已知直线y₁＝ax+b与y₂＝mx+n相交于点A（2，﹣1），若y₁＞y₂ ，则x的取值范围是x2．（填“＞”，“＜”或“＝”）

查看试题解析
18.
如图所示，购买一种苹果，所付款金额y（元）与购买量x（千克）之间的函数图象由线段OA和射线AB组成，则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省元．

查看试题解析

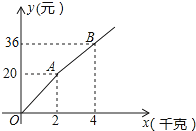
三、解答题

19. 计算：

(1)、 $(\sqrt{12} + \sqrt{20}) + (\sqrt{3} - \sqrt{5})$ ；

(2)、 $(\sqrt{8} - \sqrt{6}) \times \sqrt{3}$ ．

查看试题解析
20.

(1)、在Rt△ABC中，∠C=90°，BC=2，AB= $\sqrt{13}$ ，求AC的长；

(2)、已知△ABC中，BC=1，AC= $\sqrt{3}$ ，AB=2，求证：△ABC是直角三角形．

查看试题解析
21. 如图，直线l₁的解析式为y＝ $\frac{1}{2}$ x，直线l₂经过点（1，1），（2，﹣1），且l₁ ， l₂交于点A，l₂交x轴于点B．

(1)、求直线l₂的解析表达式；

(2)、写出B点的坐标为；

(3)、求出交点A的坐标；

(4)、直接写出直线l₂在x轴上方时，自变量x的取值范围．

查看试题解析
22. 如图，在▱ABCD中，E、F分别为边AB、CD的中点，连接DE、BF、BD．

(1)、求证：四边形DEBF为平行四边形；

(2)、当∠ADB＝90°时，求证：四边形DEBF是菱形．

查看试题解析
23. 有1号、2号两个探测气球同时出发且匀速上升，1号气球从海拔5m处出发，以1m/min的速度上升．与此同时，2号探测气球从海拔15m处出发，以0.5m/min的速度上升．设气球上升时间为xmin，

(1)、分别写出1号气球的海拔高度y₁（单位：m）、2号气球的海拔高度y₂（单位：m）与x（单位：min）的函数关系式；（不必写出x的取值范围）

(2)、气球上升多少分钟时，两个气球位于同一高度？

(3)、气球上升多少分钟时，两个气球所在位置的海拔高度相差5m？

(4)、若1号气球由于燃料消耗过快，上升40min后，减速为0.3m/min继续匀速上升，2号气球速度保持不变，设两个气球的海拔高度差为h（单位：m），请确定当40≤x≤80时，h最多为多少米？

查看试题解析