湖北省襄阳市宜城市2020-2021学年八年级上学期数学期末考试试卷

试卷更新日期：2021-03-22 类型：期末考试

进入出卷网下载

一、单选题

1. 下列运算中正确的是（）

A、 $b^{3} \cdot b^{3} = 2 b^{3}$ B、 $b^{3} \cdot b^{2} = b^{6}$ C、 ${(b^{2})}^{5} = b^{7}$ D、 $b^{2} \div b^{5} = b^{- 3}$

查看试题解析
2. 下列多项式中，能分解因式的是（）

A、 $a^{2} + b^{2}$ B、 $- a^{2} - b^{2}$ C、 $a^{2} + 4 a + 4$ D、 $a^{2} + a b + b^{2}$

查看试题解析
3. 若x²﹣kxy+9y²是一个完全平方式，则k的值为（）

A、3 B、±6 C、6 D、+3

查看试题解析
4. 若 $m n = m - n \neq 0$ ，则 $\frac{1}{m} - \frac{1}{n} =$ （）

A、-1 B、 $n - m$ C、1 D、 $\frac{1}{m n}$

查看试题解析
5. 禽流感病毒的形状一般为球形，直径大约为0.00000102m，该直径用科学记数法表示为（）

A、 $0.102 \times 10^{- 6}$ B、 $10.2 \times 10^{- 8}$ C、 $1.02 \times 10^{- 6}$ D、 $1.02 \times 10^{- 7}$

查看试题解析
6. 等腰三角形的周长是 16cm，其中一边长为4cm，则该等腰三角形的底边长为（）

A、8cm B、4cm C、10cm D、4cm或8cm

查看试题解析
7. 一个多边形的内角和是外角和的3倍，则这个多边形是（　　）

A、六边形 B、七边形 C、八边形 D、九边形

查看试题解析
8. 下列图形不是轴对称图形的是（）

A、梯形 B、圆 C、等边三角形 D、线段

查看试题解析
9. 如图，Rt△ABC中，AD是∠BAC的平分线，DE⊥AC，垂足为E.若AC=10cm，CE=4cm，则AB的长度为（）

A、10cm B、6cm C、4cm D、2cm

查看试题解析
10. 如图，四边形ABCD沿直线l对折后重合，如果 $A D / / B C$ ，则结论①AB $/ /$ CD；②AB=CD；③ $A B ⊥ B C$ ；④ $A O = O C$ 中正确的是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 计算：（a+2b）（2a﹣4b）=

查看试题解析
12. 计算： ${(\frac{2}{3})}^{2020} \times {(- 1.5)}^{2021} =$ .

查看试题解析
13. 若分式 $\frac{| x | - 3}{x - 3}$ 的值为零，则x= ．

查看试题解析
14. 如果三角形的一个外角等于与它相邻的内角的5倍，等于与它不相邻的一个内角的3倍.则此三角形最大内角是度.

查看试题解析
15. 如图，在△ABD中，AB=AD，点C在BD上（不与点B，D重合）.只需添加一个条件即可证明 $△ A B C ≌ △ A D C$ ，这个条件可以是（写出一个即可）.

查看试题解析
16. 如图，在△ABC中， $A B = A C = 10$ ， $∠ B A C = 120 °$ ，AD是△ABC的中线，AE是∠BAD的角平分线，DF//AB交AE的延长线于点F，则DF的长为.

查看试题解析

三、解答题

17. 已知 ${(m + n)}^{2} = 9, {(m - n)}^{2} = 1$ ，求 $m^{2} + n^{2} + m n$ 的值.

查看试题解析
18. 先化简，再求值： $(1 - \frac{2}{x}) \div \frac{x^{2} - 4 x + 4}{x^{2} - 4} - \frac{x + 4}{x + 2}$ .其中 $x^{2} + 2 x - 15 = 0$ .

查看试题解析
19. 如图，在△ABC中，BD 是∠ABC的角平分线. DE $/ /$ BC，交AB于点E，∠A=60°， $∠ B D C = 88 °$ ，求△BDE各内角的度数

查看试题解析
20. 观察下列算式：
① $2^{2} - 1 \times 3 = 4 - 3 = 1$ ；

② $3^{2} - 2 \times 4 = 9 - 8 = 1$ ；

③ $4^{2} - 3 \times 5 = 16 - 15 = 1$ .

(1)、请你按照三个算式的规律写出第④个、第⑤个算式：

(2)、把这个规律用含字母n的式子表示出来，并说明其正确性.

查看试题解析
21. 如图，点C在线段AB上，AD∥EB，AC=BE，AD=BC，CF平分∠DCE.试探索CF与DE的位置关系，并说明理由.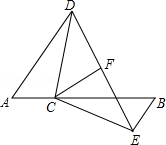

查看试题解析
22. 如图，已知A(1，2)，B(3，1)，C(4，3).

（ 1 ）作△ABC关于y轴的对称图形△A₁B₁C₁ ，写出点C关于y轴的对称点C₁的坐标；

（ 2 ）作△ABC关于直线m（直线m上各点的纵坐标都为-1）的对称图形△A₂B₂C₂ ，写出点C关于直线m的对称点C₂的坐标.

查看试题解析
23. 某超市用3000元购进某种干果销售，由于销售状况良好，超市又调拨9000元资金购进该种干果，但这次的进价比第一次的进价提高了20%，购进干果数量是第一次的2倍还多300千克，如果超市按每千克9元的价格出售，当大部分干果售出后，余下的600千克按售价的8折售完．

(1)、该种干果的第一次进价是每千克多少元？

(2)、超市销售这种干果共盈利多少元？

查看试题解析
24. 如图①，在△ABC中，AB=AC，∠BAC=90°，CD平分∠ACB， $B E ⊥ C D$ ，垂足E在 CD的延长线上. 求证∶ 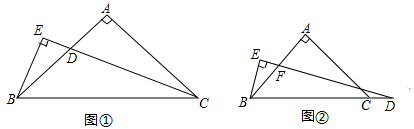$B E = \frac{1}{2} C D$ .

(1)、观察分析∶延长 BE，CA，交于点 F.可证明△_ $≌$ △ ，依据是；从而得到；再证 $B E = F E = \frac{1}{2} B F = \frac{1}{2} C D$ .

(2)、类比探究∶如图②，在△ABC中，AB=AC，∠BAC=90°，点 D在线段 BC上， $∠ B D E = \frac{1}{2} ∠ C ， B E ⊥ D E$ ，垂足为E，DE与AB相交于点F. 试探究BE与DF的数量关系，并证明你的结论.

查看试题解析
25. 如图，直线 $A B$ 分别与 $x$ 轴， $y$ 轴交于 $A 、 B$ 两点， $O C$ 平分∠ $A O B$ 交 $A B$ 于点 $C$ ，点 $D$ 为线段 $A B$ 上一点，过点 $D$ 作 $D E / / O C$ 交 $y$ 轴于点 $E$ ，已知 $A O = m ， B O = n$ ，且 $m 、 n$ 满足 $n^{2} - 12 n + 36 + | n - 2 m | = 0$ .

(1)、求 $A 、 B$ 两点的坐标；

(2)、若点 $D$ 为 $A B$ 中点，延长 $D E$ 交 $x$ 轴于点 $F$ ，在 $E D$ 的延长线上取点 $G$ ，使 $D G = D F$ ，连接 $B G$ .
① $B G$ 与 $y$ 轴的位置关系怎样？说明理由；

②求 $O F$ 的长.

查看试题解析