北京市延庆区2019-2020学年八年级下学期数学期中试卷

试卷更新日期：2021-03-22 类型：期中考试

进入出卷网下载

一、单选题

1. $\sqrt{2}$ 的相反数是（）

A、 $\sqrt{2}$ B、﹣ $\sqrt{2}$ C、2 D、﹣2

查看试题解析
2. 下列图形中，是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
3. 方程 $x^{2} - 2 x = 0$ 的解是（）

A、 $x = 2$ B、 $x_{1} = 1 ， x_{2} = 2$ C、 $x_{1} = 0 ， x_{2} = 2$ D、 $x = 0$

查看试题解析
4. 下列分式中，是最简分式的是（）

A、 $\frac{x^{2} y}{x}$ B、 $\frac{x}{x + 1}$ C、 $\frac{x + y}{x^{2} - y^{2}}$ D、 $\frac{3}{3 x - 3 y}$

查看试题解析
5. 用配方法解方程 $x^{2} - 2 x = 3$ 时，原方程应变形为（）

A、 ${(x + 1)}^{2} = 2$ B、 ${(x - 1)}^{2} = 2$ C、 ${(x + 1)}^{2} = 4$ D、 ${(x - 1)}^{2} = 4$

查看试题解析
6. 如图所示，某同学将一块三角形的玻璃打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是（）

A、带①去 B、带②去 C、带③去 D、带①②去

查看试题解析
7. 一元二次方程 $2 x^{2} - 5 x - 2 = 0$ 的根的情况是（）

A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根

查看试题解析
8. 已知 $△ A B C$ （AC＞BC），用尺规作图的方法在AB上确定一点P，使PA+PC=AB，则符合要求的作图痕迹是（）

A、 B、 C、 D、

查看试题解析

二、填空题

9. 若分式 $\frac{1}{x - 2}$ 有意义，则 $x$ 的取值范围是.

查看试题解析
10. 关于x的一元二次方程 $x^{2} - 3 x + k = 0$ 有一个根为1，则k的值等于．

查看试题解析
11. 如果等腰三角形的两条边长分别为23cm和10cm，那么第三边的长为cm．

查看试题解析
12. 若关于 $x$ 的一元二次方程 $x^{2} - 2 x + m = 0$ 有两个相等的实数根，则 $m$ 的值是．

查看试题解析
13. 在数轴上表示实数a，b的点如图所示，化简 $\sqrt{{(a - b)}^{2}}$ = ．

查看试题解析
14. 关于x的一元二次方程 $a x^{2} + b x + 2 = 0 (a \neq 0)$ 的解是 $x = 1$ ，那么2020-a-b的值是．

查看试题解析
15. 将一副三角板，按如图方式叠放，那么 $∠ α$ 的度数是．

查看试题解析
16. 根据下图中的程序，当输入一元二次方程 $x^{2} = 9$ 的解x时，输出结果 $y =$ ．

查看试题解析

三、解答题

17. 计算： $\sqrt{12} - {(3.14 - π)}^{0} + {(\sqrt{2})}^{2} + | \sqrt{3} - 1 |$ ．

查看试题解析
18. 解方程：

(1)、 $x^{2} - 2 x - 3 = 0$

(2)、 $3 {(x - 1)}^{2} = 24$

(3)、 $3 x^{2} + 2 x - 5 = 0$

查看试题解析
19. 如图，点A，F，E，D在一条直线上，AB＝CD，AF＝DE，∠BAE＝∠CDF．求证：BE=CF．

查看试题解析

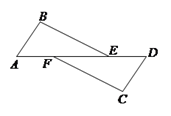20. 下面的两个题目中，请选择一个进行解答，多做不得分．

题一

题二

已知：点P(2－a，3)，且点P到x轴、y轴的距离相等．求：点P的坐标．

已知：如图，在平行四边形ABCD中， ∠ABC的平分线交AD于E，求证：AB=AE．

查看试题解析

21. 先化简，再求值： $(\frac{2 m + n}{m^{2} - m n} + \frac{1}{m}) \cdot (m^{2} - n^{2})$ ，其中 $m + n = 1$ ．

查看试题解析
22. 已知：关于 $x$ 的一元二次方程 $x^{2} - 3 x + 2 k = 0$ 有两个不相等的实数根.

(1)、求k的取值范围；

(2)、当k取最大整数值时，求该方程的解.

查看试题解析

23. 下面的两个题目中，请选择一个进行解答，多做不得分．

题一

题二

请在平面直角坐标系中，完成下面的问题

⑴描出点A(-2，3)和它关于y轴的对称点B；

⑵描出点C(2，1)和它关于原点的对

称点D；

⑶求线段AD的长．

已知：如图，E、F是平行四边形ABCD对角线AC上的两点，且AE=CF．求证：BE=DF．

查看试题解析

24. 如图，在Rt△ABC中，∠CAB =90°，BC=8 cm，∠ABC＝30°，点D从点B出发，以每秒2cm的速度在射线BA上匀速运动，当点D运动多少秒时，以C，D，B为顶点的三角形恰为等腰三角形？（结果可含根号）．

查看试题解析

25. 自2014年12月28日北京市公共电汽车和地铁按照里程分段计价．（说明：表格中“10~15公里”指的是大于10公里，小于等于15公里，其他类似）

北京公交车新票价
里程范围	对应票价
0~10公里	2元
10~15公里	3元
15~20公里	4元
20公里以上	每增加1元可再乘坐5公里（不足5公里按5公里计算）
*持市政交通一卡通刷卡，普通卡打5折，学生卡打2.5折

小明办了一张市政交通一卡通学生卡．

(1)、如果小明全程乘坐公交车的里程为17公里，用他的学生卡刷卡，需交费元；

(2)、小明周末和妈妈一起去离他家50公里的莲花山公园游玩，他用学生卡，妈妈用普通卡，请通过计算说明，此次出行小明和妈妈的单程车费一共是多少元？

(3)、小明乘坐公交车前往区图书馆，请表示他此次出行单程的公交费用y（元）与行驶里程x公里（

17 < x \leq 30

且为整数）之间的数量关系．

查看试题解析

26. 下面的两个题目中，请选择一个进行解答，多做不得分．

题一

题二

一个函数的图象如图所示，根据图象回答问题

⑴写出自变量x的取值范围；

⑵当x=18时，则y的值是多少；

⑶求 $△ A B O$ 的面积；

⑷当 $18 \leq x \leq 23$ 时，请说明：当x的值逐渐变大时，函数值y怎样变化？

已知：在 $△ A B C$ 中，AB=AC，DE∥AB，DF∥AC．求证：AC=DE+DF．

查看试题解析

27. 如图1，△ABC是等边三角形，点D，E分别是BC，AB上的点，且BD=AE，AD与CE交于点F．

(1)、求∠DFC的度数；

(2)、将CE绕着点C逆时针旋转120°，得到CP，连接AP，交BC于点Q．
①补全图形（图2中完成）；

②用等式表示线段BE与CQ的数量关系，并证明．

查看试题解析