湖北省武汉市新洲区2020-2021学年八年级上学期数学期末考试试卷
试卷更新日期:2021-03-22 类型:期末考试
一、单选题
-
1. 现实世界中,对称现象无处不在,中国的方块字中有些也只有对称性,下列汉字是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 以下长度的三条线段,不能组成三角形的是( )A、3、8、2 B、2、5、4 C、6、3、5 D、9、15、73. 五边形的外角和等于( )
2. 以下长度的三条线段,不能组成三角形的是( )A、3、8、2 B、2、5、4 C、6、3、5 D、9、15、73. 五边形的外角和等于( )
A、180° B、360 ° C、540° D、720°4. 如图,要在三条交错的公路区域附近修建一个物流公司仓库,使仓库到三条公路的距离相等,则可以选择的地址有( )处 A、1 B、2 C、3 D、45. 如图,两个三角形全等,则 等于( )
A、1 B、2 C、3 D、45. 如图,两个三角形全等,则 等于( ) A、 B、 C、 D、6. 点 关于y轴对称的点的坐标为( )A、 B、 C、 D、7. 用直尺和圆规作一个角等于已知角,如图,能得出∠A′O′B′=∠AOB的依据是( )
A、 B、 C、 D、6. 点 关于y轴对称的点的坐标为( )A、 B、 C、 D、7. 用直尺和圆规作一个角等于已知角,如图,能得出∠A′O′B′=∠AOB的依据是( )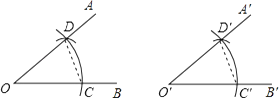 A、SSS B、SAS C、ASA D、AAS8. 如图,在4×3的长方形网格中,已知A、B两点为格点(网格线的交点称为格点),若C也为该网格中的格点,且△ABC为等腰直角三角形,则格点C的个数为( )
A、SSS B、SAS C、ASA D、AAS8. 如图,在4×3的长方形网格中,已知A、B两点为格点(网格线的交点称为格点),若C也为该网格中的格点,且△ABC为等腰直角三角形,则格点C的个数为( ) A、2 B、4 C、6 D、89. 如图, 中, 、 为线段 BC 上两点,且 , ,若 ,则 的度数为( )
A、2 B、4 C、6 D、89. 如图, 中, 、 为线段 BC 上两点,且 , ,若 ,则 的度数为( ) A、 B、 C、 D、10. 如图,在 中, , , 平分 交 于 , 于 , 交 的延长线于 ,连接 ,给出四个结论:① ;② ;③ ;④ ;其中正确的结论有( )
A、 B、 C、 D、10. 如图,在 中, , , 平分 交 于 , 于 , 交 的延长线于 ,连接 ,给出四个结论:① ;② ;③ ;④ ;其中正确的结论有( )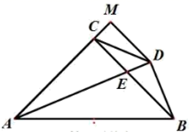 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 如图,要使五边形木架不变形,至少要再钉上根木条.
 12. 六边形的对角线有 条.13. 如图的三角形纸片中,AB=8cm,BC=6cm,AC=5cm.点D是AC上一点,沿过BD折叠,使点C落在AB上的点E处,则 AED的周长为cm.
12. 六边形的对角线有 条.13. 如图的三角形纸片中,AB=8cm,BC=6cm,AC=5cm.点D是AC上一点,沿过BD折叠,使点C落在AB上的点E处,则 AED的周长为cm.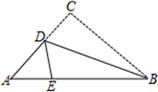 14. 等腰三角形一腰上的高与另一腰的夹角为 ,则这个等腰三角形的底角度数为.15. 如图,△ABC中,AB=8,BC=10,AC=7,∠ABC和∠ACB的平分线交于点I,IE⊥BC于E,则BE的长为.
14. 等腰三角形一腰上的高与另一腰的夹角为 ,则这个等腰三角形的底角度数为.15. 如图,△ABC中,AB=8,BC=10,AC=7,∠ABC和∠ACB的平分线交于点I,IE⊥BC于E,则BE的长为.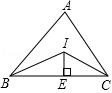 16. 如图,在△ABC 中,∠ABC=57°, ∠BAD=71° ,∠DAC=30° ,∠ACD=11° ,求∠DBC 的度数.
16. 如图,在△ABC 中,∠ABC=57°, ∠BAD=71° ,∠DAC=30° ,∠ACD=11° ,求∠DBC 的度数.
三、解答题
-
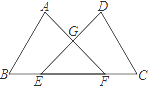
17. 如图,点E、F在BC上,BE=CF,AB=DC,∠B=∠C,AF与DE交于点G,求证:GE=GF.
 18. 已知:如图,E为BC上一点,AC∥BD.AC=BE.BC=BD.求证:AB=DE.
18. 已知:如图,E为BC上一点,AC∥BD.AC=BE.BC=BD.求证:AB=DE. 19. 如图.△ABC中,CA=CB.D是AB的中点.∠CED=∠CFD=90°,CE=CF,求证:∠ADF=∠BDE.
19. 如图.△ABC中,CA=CB.D是AB的中点.∠CED=∠CFD=90°,CE=CF,求证:∠ADF=∠BDE.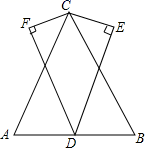 20. 如图所示, 在平面直角坐标系中(每个小正方形的边长为1个单位长度)
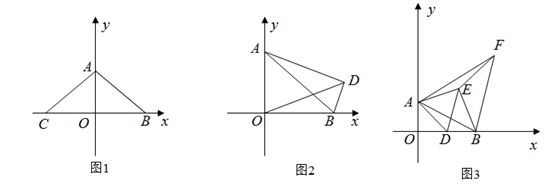
20. 如图所示, 在平面直角坐标系中(每个小正方形的边长为1个单位长度) (1)、直接写出点 的坐标 ( , );(2)、画出 关于 轴对称的 ;(3)、将 向右平移7个单位,画出平移后的 ,指出 与 位置关于 对称.21. 如图, , , .
(1)、直接写出点 的坐标 ( , );(2)、画出 关于 轴对称的 ;(3)、将 向右平移7个单位,画出平移后的 ,指出 与 位置关于 对称.21. 如图, , , . (1)、求证: ;(2)、若 ,试判断 与 的数量及位置关系并证明;(3)、若 ,求 的度数.22. 如图, 中, , .
(1)、求证: ;(2)、若 ,试判断 与 的数量及位置关系并证明;(3)、若 ,求 的度数.22. 如图, 中, , . (1)、如图1, , ,求证: ;(2)、如图2, , ,请直接用几何语言写出 、 的位置关系;(3)、证明(2)中的结论.
(1)、如图1, , ,求证: ;(2)、如图2, , ,请直接用几何语言写出 、 的位置关系;(3)、证明(2)中的结论.