上海市徐汇区2021年中考数学一模试卷
试卷更新日期:2021-03-22 类型:中考模拟
一、单选题
-
1. 将抛物线 先向右平移 个单位,再向下平移 个单位后,所得抛物线的表达式是( )A、 B、 C、 D、2. 在 中, , , ,那么下列结论正确的是( )A、 B、 C、 D、3. 已知抛物线 经过点 ,那么下列各点中,该抛物线必经过的点是( )A、 B、 C、 D、4. 已知海面上一艘货轮 在灯塔 的北偏东 方向,海监船 在灯塔 的正东方向 海里处,此时海监船 发现货轮 在它的正北方向,那么海监船 与货轮 的距离是( )A、 海里 B、 海里 C、 海里 D、 海里5. 下列说法中,正确的是( )A、两个矩形必相似 B、两个含 角的等腰三角形必相似 C、两个菱形必相似 D、两个含 角的直角三角形必相似6. 定义: 表示不超过实数 的最大整数例如: , , 根据你学习函数的经验,下列关于函数 的判断中,正确的是( )A、函数 的定义域是一切整数 B、函数 的图像是经过原点的一条直线 C、点 在函数 图像上 D、函数 的函数值 随 的增大而增大
二、填空题
-
7. 如果 ,那么代数式 的值是 .8. 如图, ,如果 , , ,那么 的长是 .
 9. 已知点 在线段 上,如果 , ,那么 的长是 .10. 已知二次函数 的图像在直线 的左侧部分是下降的,那么a的取值范围是 .11. 如图,在 中,点 分别在边 上, ,如果 和四边形 的面积相等, ,那么 DE的长是 .
9. 已知点 在线段 上,如果 , ,那么 的长是 .10. 已知二次函数 的图像在直线 的左侧部分是下降的,那么a的取值范围是 .11. 如图,在 中,点 分别在边 上, ,如果 和四边形 的面积相等, ,那么 DE的长是 . 12.
12.如图,在坡度为1:3的山坡上种树,要求株距(相邻两树间的水平距离)是6米,则斜坡上相邻两树间的坡面距离是米(结果保留根号)
 13. 已知甲、乙两楼相距 米,如果从甲楼底看乙楼顶,测得仰角为 ,从乙楼顶看甲楼顶,测得俯角为 ,那么甲楼高是米.14. 如图,点 在线段 上, , , ,如果 , , ,那么 的长是 .
13. 已知甲、乙两楼相距 米,如果从甲楼底看乙楼顶,测得仰角为 ,从乙楼顶看甲楼顶,测得俯角为 ,那么甲楼高是米.14. 如图,点 在线段 上, , , ,如果 , , ,那么 的长是 .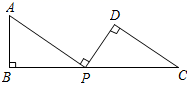 15. 如图,已知 是边长为 的等边三角形,正方形 的顶点 分别在边 上,点 在边 上,那么 的长是 .
15. 如图,已知 是边长为 的等边三角形,正方形 的顶点 分别在边 上,点 在边 上,那么 的长是 . 16. 《周髀算经》中的“赵爽弦图”(如图),图中的四个直角三角形都全等,如果正方形 的面积是正方形 面积的 倍,那么 的余切值是 .
16. 《周髀算经》中的“赵爽弦图”(如图),图中的四个直角三角形都全等,如果正方形 的面积是正方形 面积的 倍,那么 的余切值是 . 17. 如图,在 中,点 分别在边 、 上, ,将 沿直线 翻折后与 重合, 、 分别与边 交于点 、 ,如果 , ,那么 的长是 .
17. 如图,在 中,点 分别在边 、 上, ,将 沿直线 翻折后与 重合, 、 分别与边 交于点 、 ,如果 , ,那么 的长是 . 18. 如图,在 中, , ,点 在边 上,点 在边 上, , ,如果 的面积是 ,那么 的长是 .
18. 如图,在 中, , ,点 在边 上,点 在边 上, , ,如果 的面积是 ,那么 的长是 .
三、解答题
-
19. 计算: .20. 如图,在 中, 平分 , 与 交于点 , , .
 (1)、求 的值;(2)、设 , = ,求向量 (用向量 、 表示).21. 已知抛物线 与 轴交于点 ,它的顶点为 ,对称轴是直线 .(1)、求此抛物线的表达式及点 的坐标;(2)、将上述抛物线向下平移 个单位,所得新抛物线经过原点 ,设新抛物线的顶点为 ,请判断 的形状,并说明理由.22. 为加强对市内道路交通安全的监督,王警官利用无人机进行检测.某高架路有一段限速每小时 千米的道路 (如图所示),当无人机在限速道路的正上方 处时,测得限速道路的起点 的俯角是 ,无人机继续向右水平飞行 米到达 处,此时又测得起点 的俯角是 ,同时测得限速道路终点 的俯角是 (注:即四边形 是梯形).
(1)、求 的值;(2)、设 , = ,求向量 (用向量 、 表示).21. 已知抛物线 与 轴交于点 ,它的顶点为 ,对称轴是直线 .(1)、求此抛物线的表达式及点 的坐标;(2)、将上述抛物线向下平移 个单位,所得新抛物线经过原点 ,设新抛物线的顶点为 ,请判断 的形状,并说明理由.22. 为加强对市内道路交通安全的监督,王警官利用无人机进行检测.某高架路有一段限速每小时 千米的道路 (如图所示),当无人机在限速道路的正上方 处时,测得限速道路的起点 的俯角是 ,无人机继续向右水平飞行 米到达 处,此时又测得起点 的俯角是 ,同时测得限速道路终点 的俯角是 (注:即四边形 是梯形).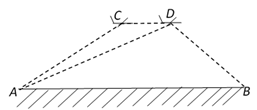 (1)、求限速道路 的长(精确到 米);(2)、如果李师傅在道路 上行驶的时间是 分 秒,请判断他是否超速?并说明理由.(参考数据: , , , )23. 如图,在 中,点 、 分别在边 、 上, , , 与 交于点 ,且 .
(1)、求限速道路 的长(精确到 米);(2)、如果李师傅在道路 上行驶的时间是 分 秒,请判断他是否超速?并说明理由.(参考数据: , , , )23. 如图,在 中,点 、 分别在边 、 上, , , 与 交于点 ,且 .
求证:
(1)、 ;(2)、 .24. 已知二次函数 的大致图像如图所示,这个函数图象的顶点为点 . (1)、求该函数图象的开口方向、对称轴及点 的坐标;(2)、设该函数图象与 轴正半轴交于点 ,与 轴正半轴交于点 ,图像的对称轴与 轴交于点 ,如果 , ,求该二次函数的解析式;(3)、在(2)的条件下,设点 在第一象限该函数的图象上,且点 的横坐标为 ,如果 的面积是 ,求点 的坐标.25. 如图,在 中, , , ,点 是边 上的动点,以 为边在 外作正方形 ,分别联结 、 , 与 交于点 .
(1)、求该函数图象的开口方向、对称轴及点 的坐标;(2)、设该函数图象与 轴正半轴交于点 ,与 轴正半轴交于点 ,图像的对称轴与 轴交于点 ,如果 , ,求该二次函数的解析式;(3)、在(2)的条件下,设点 在第一象限该函数的图象上,且点 的横坐标为 ,如果 的面积是 ,求点 的坐标.25. 如图,在 中, , , ,点 是边 上的动点,以 为边在 外作正方形 ,分别联结 、 , 与 交于点 . (1)、当 时,求正方形 的面积;(2)、延长 交 于点 ,如果 和 相似,求 的值;(3)、当 时,求 的长.
(1)、当 时,求正方形 的面积;(2)、延长 交 于点 ,如果 和 相似,求 的值;(3)、当 时,求 的长.