上海市浦东新区2021年中考数学一模试卷

试卷更新日期：2021-03-22 类型：中考模拟

进入出卷网下载

一、单选题

1. A、B两地的实际距离AB=250米，如果画在地图上的距离 $A^{'} B^{'}$ =5厘米，那么地图上的距离与实际距离的比为（）

A、1∶500 B、1∶5 000 C、500∶1 D、5 000∶1

查看试题解析
2. 已知在 $R t Δ A B C$ 中， $∠ C = 90 °$ ， $∠ A = α ， B C = 2$ ，那么AB的长等于（）

A、 $\frac{2}{\sin α}$ B、 $2 \sin α$ C、 $\frac{2}{\cos α}$ D、 $2 \cos α$

查看试题解析
3. 下列 $y$ 关于x的函数中，一定是二次函数的是（）

A、 $y = (k - 1) x^{2} + 3$ B、 $y = \frac{1}{x^{2}} + 1$ C、 $y = (x + 1) (x - 2) - x^{2}$ D、 $y = 2 x^{2} - 7 x$

查看试题解析
4. 已知一个单位向量 $\overset{⇀}{e}$ ，设 $\overset{⇀}{a}$ 、 $\overset{⇀}{b}$ 是非零向量，那么下列等式中正确的是（）．

A、 $\frac{1}{| \vec{a} |} \vec{a} = \vec{e}$ ； B、 $| \vec{e} | \vec{a} = \vec{a}$ ； C、 $| \vec{b} | \vec{e} = \vec{b}$ ； D、 $\frac{1}{| \vec{a} |} \vec{a} = \frac{1}{| \vec{b} |} \vec{b}$ ．

查看试题解析
5. 如图，在 $△$ ABC中，点D、F是边AB上的点，点E是边AC上的点，如果∠ACD=∠B，DE $/ /$ BC，EF $/ /$ CD，下列结论不成立的是（）

A、 $A E^{2} = A F \cdot A D$ B、 $A C^{2} = A D \cdot A B$ C、 $A F^{2} = A E \cdot A C$ D、 $A D^{2} = A F \cdot A B$

查看试题解析
6. 已知点A（1，2）、B（2，3）、C（2，1），那么抛物线 $y = a x^{2} + b x + 1$ 可以经过的点是（）

A、点A、B、C B、点A、B C、点A、C D、点B、C

查看试题解析

二、填空题

7. 如果线段a、b满足 $\frac{a}{b} = \frac{5}{2}$ ，那么 $\frac{a - b}{b}$ 的值等于．

查看试题解析
8. 已知线段MN的长是4cm，点P是线段MN的黄金分割点，则较长线段MP的长是cm．

查看试题解析
9. 计算： $2 \sin 30^{\circ} - \tan 45^{\circ} =$ ．

查看试题解析
10. 如果从某一高处甲看低处乙的俯角为36度，那么从低处乙看高处甲的仰角是度．

查看试题解析
11. 已知AD、BE是 $△$ ABC的中线，AD、BE相交于点F，如果AD=3，那么AF= ．

查看试题解析
12. 如图，已知平行四边形ABCD的对角线AC与BD相交于点O，设 $\vec{O A} = \vec{a}$ ， $\vec{O B} = \vec{b}$ ，那么向量 $\vec{A B}$ 关于 $\vec{a}$ 、 $\vec{b}$ 的分解式为．

查看试题解析
13. 如果抛物线 $y = (m + 4) x^{2} + m$ 经过原点，那么该抛物线的开口方向．（填“向上”或“向下”）

查看试题解析
14. 如果（2， $y_{1}$ ）、（3， $y_{2}$ ）是抛物线 $y = {(x + 1)}^{2}$ 上两点，那么 $y_{1}$ $y_{2}$ ．（填“>”或“<”）

查看试题解析
15. 如图，矩形DEFG的边EF在 $△$ ABC的边BC上，顶点D、G分别在边AB、AC上，已知 $△$ ABC的边BC长60厘米，高AH为40厘米，如果DE=2DG，那么DG=厘米．

查看试题解析
16. 秦九韶的《数书九章》中有一个“峻积验雪”的例子，其原理为：如图，在Rt $△$ ABC中，∠C=90°，AC=12，BC=5，AD⊥AB，AD=0.4，过点D作DE $/ /$ AB交CB的延长线于点E，过点B作BF⊥CE交DE于点F，那么BF= ．

查看试题解析
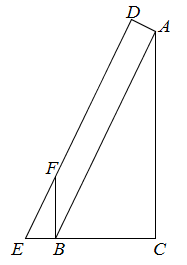17. 如果将二次函数的图象平移，有一个点既在平移前的函数图象上又在平移后的函数图象上，那么称这个点为“平衡点”．现将抛物线 $C_{1}$ ： $y = {(x - 1)}^{2} - 1$ 向右平移得到新抛物线 $C_{2}$ ，如果“平衡点”为（3，3），那么新抛物线 $C_{2}$ 的表达式为．

查看试题解析
18. 如图， $△$ ABC中，AB=10，BC=12，AC=8，点D是边BC上一点，且BD：CD=2：1，联结AD，过AD中点M的直线将 $△$ ABC分成周长相等的两部分，这条直线分别与边BC、AC相交于点E、F，那么线段BE的长为．

查看试题解析

三、解答题

19. 已知向量关系式 $\frac{1}{2} (\vec{a} - \vec{x}) = \vec{b} + 3 \vec{x}$ ，试用向量 $\vec{a}$ 、 $\vec{b}$ 表示向量 $\vec{x}$ ．

查看试题解析
20. 已知抛物线 $y = x^{2} + 2 x + m - 3$ 的顶点在第二象限，求 $m$ 的取值范围．

查看试题解析
21. 如图，已知AD $/ /$ BE $/ /$ CF，它们依次交直线 $l_{1}$ 、 $l_{2}$ 于点A、B、C和点D、E、F，且AB=6，BC=8．

(1)、求 $\frac{D E}{D F}$ 的值；

(2)、当AD=5，CF=19时，求BE的长．

查看试题解析
22. 如图，燕尾槽的横断面是等腰梯形ABCD，现将一根木棒MN放置在该燕尾槽中，木棒与横断面在同一平面内，厚度等不计，它的底端N与点C重合，且经过点A．已知燕尾角∠B=54.5°，外口宽AD=180毫米，木棒与外口的夹角∠MAE=26.5°，求燕尾槽的里口宽BC（精确到1毫米）．（参考数据： $\sin 54.5 ° \approx 0.81$ ， $\cos 54.5 ° \approx 0.58$ ， $\tan 54.5 ° \approx 1.40$ ， $\sin 26.5 ° \approx 0.45$ ， $\cos 26.5 ° \approx 0.89$ ， $\tan 26.5 ° \approx 0.50$ ）

查看试题解析
23. Rt $△$ ABC中，∠ACB=90°，点D、E分别为边AB、BC上的点，且CD=CA，DE⊥AB．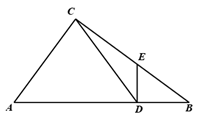

(1)、求证： $C A^{2} = C E \cdot C B$ ．

(2)、联结AE，取AE的中点M，联结CM并延长与AB交于点H．求证：CH⊥AB．

查看试题解析
24. 二次函数 $y = a x^{2} + b x + c$ （ $a \neq 0$ ）的图像经过点A（2，4）、B（5，0）和O（0，0）．

(1)、求二次函数的解析式；

(2)、联结AO，过点B作BC⊥AO于点C，与该二次函数图象的对称轴交于点P，联结AP，求∠BAP的余切值；

(3)、在（2）的条件下，点M在经过点A且与x轴垂直的直线上，当 $△$ AMO与 $△$ ABP相似时，求点M的坐标．

查看试题解析
25. 四边形ABCD是菱形，∠B≤90°，点E为边BC上一点，联结AE，过点E作EF⊥AE，EF与边CD交于点F，且EC=3CF．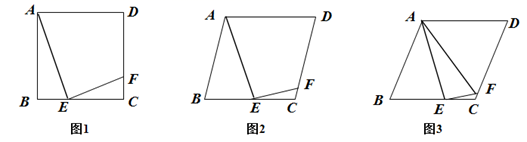

(1)、如图1，当∠B=90°时，求 $S_{△ A B E}$ 与 $S_{△ E C F}$ 的比值；

(2)、如图2，当点E是边BC的中点时，求 $\cos B$ 的值；

(3)、如图3，联结AF，当∠AFE=∠B且CF=2时，求菱形的边长．

查看试题解析