上海市静安区2021年中考数学一模试卷

试卷更新日期：2021-03-22 类型：中考模拟

进入出卷网下载

一、单选题

1. 如果 $a \neq 0$ ，那么下列计算正确的是（）

A、 ${(- a)}^{0} = 0$ B、 ${(- a)}^{0} = - 1$ C、 $- a^{0} = 1$ D、 $- a^{0} = - 1$

查看试题解析
2. 下列多项式中，是完全平方式的为（）

A、 $x^{2} - x + \frac{1}{4}$ B、 $x^{2} + \frac{1}{2} x + \frac{1}{4}$ C、 $x^{2} + \frac{1}{4} x - \frac{1}{4}$ D、 $x^{2} - \frac{1}{4} x + \frac{1}{4}$

查看试题解析
3. 将抛物线 $y = 2 {(x + 1)}^{2} - 3$ 平移后与抛物线 $y = 2 x^{2}$ 重合，那么平移的方法可以是（）

A、向右平移1个单位，再向上平移3个单位 B、向右平移1个单位，再向下平移3个单位 C、向左平移1个单位，再向上平移3个单位 D、向左平移1个单位，再向下平移3个单位

查看试题解析
4. 在△ABC中，点D、E分别在边BA、CA的延长线上，下列比例式中能判定DE∥BC的为（）

A、 $\frac{B C}{D E} = \frac{AB}{AD}$ B、 $\frac{AC}{AD} = \frac{A B}{A E}$ C、 $\frac{AC}{CE} = \frac{A B}{B D}$ D、 $\frac{AC}{AB} = \frac{B D}{C E}$

查看试题解析
5. 如果锐角 $α$ 的正切值为 $\frac{\sqrt{3}}{2}$ ，那么下列结论中正确的是（）

A、 $α = 30 °$ B、 $α = 60 °$ C、 $30 ° < α < 45 °$ D、 $45 ° < α < 60 °$

查看试题解析
6. 在Rt△ABC中，∠C=90°，CD是高，如果AB=m，∠A= $α$ ，那么CD的长为（）

A、 $m \cdot \sin α \cdot \tan α$ B、 $m \cdot \sin α \cdot \cos α$ C、 $m \cdot \cos α \cdot \tan α$ D、 $m \cdot \cos α \cdot \cot α$

查看试题解析

二、填空题

7. $\frac{3}{2}$ 的相反数是．

查看试题解析
8. 函数 $f (x) = \frac{x - 1}{\sqrt{2 - x}}$ 的定义域为．

查看试题解析
9. 方程 $\sqrt{3 - 2 x} = 2 - x$ 的根为．

查看试题解析
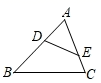
10. 二次函数 $y = 2 x - 3 x^{2}$ 图像的开口方向是．

查看试题解析
11. 抛物线 $y = 3 x^{2} - 6$ 的顶点坐标为．

查看试题解析
12. 如果一次函数 $y = (m - 2) x + m - 1$ 的图像经过第一、二、四象限，那么常数 $m$ 的取值范围为．

查看试题解析
13. 在二次函数 $y = x^{2} - 2 x + 3$ 图像的上升部分所对应的自变量x的取值范围是．

查看试题解析
14. 如图，在△ABC中，点D、E分别在边AB、AC上，∠AED=∠B，如果AD=2，AE=3，CE=1，那么BD长为．

查看试题解析
15. 在△ABC中，点G是重心，∠BGC=90°，BC=8，那么AG的长为．

查看试题解析
16. 如图，在△ABC中，点D、E分别在边AB、AC上，DE∥BC，如果AB=12，BC=9，AC=6，四边形BCED的周长为21，那么DE的长为．

查看试题解析
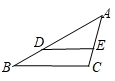17. 如图，在梯形ABCD中，AD∥BC，BD与AC相交于点O，OB=2OD，设 $\vec{A B} = \vec{a}$ ， $\vec{AD} = \vec{b}$ ，那么 $\vec{AO} =$ ．（用向量 $\vec{a}$ 、 $\vec{b}$ 的式子表示）

查看试题解析
18. 在Rt△ABC中，∠C=90°，AB=13， $\tan B = \frac{2}{3}$ （如图），将△ABC绕点C旋转后，点A落在斜边AB上的点A’，点B落在点B’，A’B’与边BC相交于点D，那么 $\frac{CD}{A'D}$ 的值为．

查看试题解析

三、解答题

19. 计算： $\frac{\cot 30 ° - \cos 45 °}{\sin 60 ° - \tan 45 °}$ ．

查看试题解析
20. 已知线段x、y满足 $\frac{2 x + y}{x - y} = \frac{x}{y} ，$ 求 $\frac{x}{y}$ 的值．

查看试题解析
21. 如图，点A、B在第一象限的反比例函数图象上，AB的延长线与y轴交于点C，已知点A、B的横坐标分别为6、2，AB= $2 \sqrt{5}$ ．

(1)、求∠ACO的余弦值；

(2)、求这个反比例函数的解析式．

查看试题解析
22. 如图，一处地铁出入口的无障碍通道是转折的斜坡，沿着坡度相同的斜坡BC、CD共走7米可到出入口，出入口点D距离地面的高DA为0.8米，求无障碍通道斜坡的坡度与坡角（角度精确到1'，其他近似数取四个有效数字）．

查看试题解析
23. 已知：如图，在△ABC中，DE∥BC，AD²=AE•AC．求证：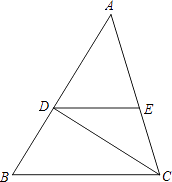

(1)、△BCD∽△CDE；

(2)、 $\frac{C D^{2}}{B C^{2}} = \frac{A D}{A B}$ ．

查看试题解析
24. 如图，在平面直角坐标系xOy中，直线 $y = - \frac{1}{2} x + m (m > 0)$ 与x轴、y轴分别交于点A、B．抛物线 $y = a x^{2} + b x + 4$ （a≠0）经过点A，且与y轴相交于点C，∠OCA=∠OAB．

(1)、求直线AB的表达式；

(2)、如果点D在线段AB的延长线上，且AD=AC．求经过点D的抛物线 $y = a x^{2} + b x + 4$ 的表达式；

(3)、如果抛物线 $y = a x^{2} + b x + 4$ 的对称轴与线段AB、AC分别相交于点E、F，且EF=1，求此抛物线的顶点坐标．

查看试题解析
25. 已知∠MAN是锐角，点B、C在边AM上，点D在边AN上，∠EBD=∠MAN，且CE∥BD，sin∠MAN= $\frac{3}{5}$ ， AB=5，AC=9．

(1)、如图1，当CE与边AN相交于点F时，求证：DF·CE=BC·BE；

(2)、当点E在边AN上时，求AD的长；

(3)、当点E在∠MAN外部时，设AD=x，△BCE的面积为y，求y与x之间的函数解析式，并写出定义域．

查看试题解析