广西壮族自治区河池市南丹县2020-2021学年八年级上学期数学期末考试试卷
试卷更新日期:2021-03-22 类型:期末考试
一、单选题
-
1. 下列各式中属于最简分式的是( )A、 B、a+b C、 D、2. 人字梯中间一般会设计一”拉杆”,这样做的道理是( ).
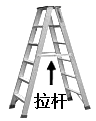 A、两点之间,线段最短 B、垂线段最短 C、两直线平行,内错角相等 D、三角形具有稳定性3. 下列四个图案中,不是轴对称图案的是( )A、
A、两点之间,线段最短 B、垂线段最短 C、两直线平行,内错角相等 D、三角形具有稳定性3. 下列四个图案中,不是轴对称图案的是( )A、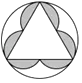 B、
B、 C、
C、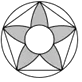 D、
D、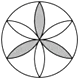 4. 数据0.0000000 14用科学记数法表示为( )A、 B、 C、 D、5. 如图,在 中,点 在 的延长线上,若 , ,则 的度数是( )
4. 数据0.0000000 14用科学记数法表示为( )A、 B、 C、 D、5. 如图,在 中,点 在 的延长线上,若 , ,则 的度数是( ) A、 B、 C、 D、6. 下列计算正确的是( )A、 B、 C、 D、7. 如图,若 ,则 的度数是( )
A、 B、 C、 D、6. 下列计算正确的是( )A、 B、 C、 D、7. 如图,若 ,则 的度数是( )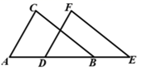 A、 B、 C、 D、8. 若把分式 的 和 都扩大5倍,则分式的值( )A、扩大到原来的5倍 B、不变 C、缩小为原来的 倍 D、扩大到原来的25倍9. 将一副三角板按如图所示的方式放置,图中∠CAF的大小等于( )
A、 B、 C、 D、8. 若把分式 的 和 都扩大5倍,则分式的值( )A、扩大到原来的5倍 B、不变 C、缩小为原来的 倍 D、扩大到原来的25倍9. 将一副三角板按如图所示的方式放置,图中∠CAF的大小等于( )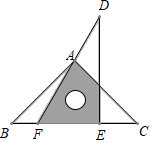 A、50° B、60° C、75° D、85°10. 如图, 平分 , , ,垂足分别为 、 ,若 ,则 ( )
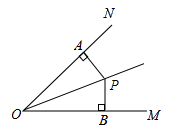
A、50° B、60° C、75° D、85°10. 如图, 平分 , , ,垂足分别为 、 ,若 ,则 ( )
 A、 B、 C、 D、11. 已知 ,则 的值为( )A、6 B、5 C、3 D、112. 如图,BE,CF都是△ABC的角平分线,且∠BDC=110°,则∠A的度数为( )
A、 B、 C、 D、11. 已知 ,则 的值为( )A、6 B、5 C、3 D、112. 如图,BE,CF都是△ABC的角平分线,且∠BDC=110°,则∠A的度数为( ) A、40° B、50° C、60° D、70°
A、40° B、50° C、60° D、70°二、填空题
-
13. 如图,已知△ABC≌△DEF,则DE=.
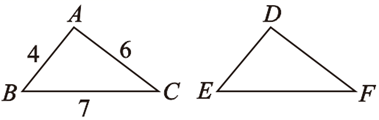 14. 若分式 有意义,则 的取值范围是 .15. 因式分解:16. 一个多边形的每个外角都等于60°,则这个多边形的边数是。17. 如图所示,在Rt△ABC中,∠C=90°,∠A=15°,将△ABC翻折,是顶点A与顶点B重合,折痕为MH,已知AH=2,则BC等于.
14. 若分式 有意义,则 的取值范围是 .15. 因式分解:16. 一个多边形的每个外角都等于60°,则这个多边形的边数是。17. 如图所示,在Rt△ABC中,∠C=90°,∠A=15°,将△ABC翻折,是顶点A与顶点B重合,折痕为MH,已知AH=2,则BC等于.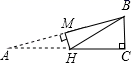 18. 如图,已知AB=AC,AD=BD=BC.在BC延长线上取点C1 , 连接DC1 , 使DC=CC1 , 在CC1延长线上取点C2 , 在DC1上取点E,使EC1=C1C2 , 同理FC2=C2C3 , 若继续如此下去直到C2021 , 则∠C2021的度数为.
18. 如图,已知AB=AC,AD=BD=BC.在BC延长线上取点C1 , 连接DC1 , 使DC=CC1 , 在CC1延长线上取点C2 , 在DC1上取点E,使EC1=C1C2 , 同理FC2=C2C3 , 若继续如此下去直到C2021 , 则∠C2021的度数为.
三、解答题
-
19. 计算:(1)、 ;(2)、20. 解分式方程:21. 先化简,再求值:
(2a+b)(2a-b)+b(2a+b)-4a2b÷b,其中a=- ,b=2
22. 如图,在平面直角坐标系xOy中,A(-1,5),B(-1,0),C(-4,3). (1)、在图中作出△ABC关于y轴的对称图形△A1B1C1;(2)、写出点A1 , B1 , C1的坐标;(3)、求出△A1B1C1的面积.23. 如图,在△ABC中,AB=AC,DE垂直平分AB.
(1)、在图中作出△ABC关于y轴的对称图形△A1B1C1;(2)、写出点A1 , B1 , C1的坐标;(3)、求出△A1B1C1的面积.23. 如图,在△ABC中,AB=AC,DE垂直平分AB.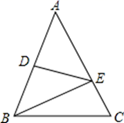 (1)、若AB=AC=10cm,BC=6cm,求△BCE的周长;(2)、若∠A=40°,求∠EBC的度数.24. 如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.
(1)、若AB=AC=10cm,BC=6cm,求△BCE的周长;(2)、若∠A=40°,求∠EBC的度数.24. 如图,已知AC⊥BC,BD⊥AD,AC与BD交于O,AC=BD.
求证:
(1)、BC=AD;(2)、△OAB是等腰三角形.25. 五月初,我市多地遭遇了持续强降雨的恶劣天气,造成部分地区出现严重洪涝灾害,某爱心组织紧急筹集了部分资金,计划购买甲、乙两种救灾物品共2000件送往灾区,已知每件甲种物品的价格比每件乙种物品的价格贵10元,用350元购买甲种物品的件数恰好与用300元购买乙种物品的件数相同(1)、求甲、乙两种救灾物品每件的价格各是多少元?(2)、经调查,灾区对乙种物品件数的需求量是甲种物品件数的3倍,若该爱心组织按照此需求的比例购买这2000件物品,需筹集资金多少元?26. 如图(1) , ,BD⊥AB, ,点 在线段 上以 的速度由点 向点 运动,同时,点 在线段 上由点 向点 运动,它们运动的时间为 .
 (1)、若点 的速度与点 的速度相等,当 时,求证: ;(2)、在(1)的条件下,判断此时 和 的位置关系,并证明;(3)、将图(1)中的“ , ”,改为“ ”,得到图(2),其他条件不变.设点 的运动速度为 ,请问是否存在实数 ,使得 与 全等?若存在,求出相应的 和 的值;若不存在,请说明理由.
(1)、若点 的速度与点 的速度相等,当 时,求证: ;(2)、在(1)的条件下,判断此时 和 的位置关系,并证明;(3)、将图(1)中的“ , ”,改为“ ”,得到图(2),其他条件不变.设点 的运动速度为 ,请问是否存在实数 ,使得 与 全等?若存在,求出相应的 和 的值;若不存在,请说明理由.