甘肃省金昌市联考2020-2021学年八年级上学期数学期末考试试卷
试卷更新日期:2021-03-22 类型:期末考试
一、单选题
-
1. 若代数式 有意义,则实数 的取值范围是( )A、 B、 C、 D、2. 在长为10cm , 7cm , 5cm , 3cm的四根木条,选其中三根组成三角形,则能组成三角形的个数为( )A、1 B、2 C、3 D、43. 下列各式变形中,是因式分解的是( )A、 B、 C、 D、4. 下列分式中,不是最简分式的是( )A、 B、 C、 D、5. 已知三角形的三个外角的度数比为2:3:4,则它的最大内角的度数为( )A、90° B、110° C、100° D、120°6. 已知:点A(m﹣1,3)与点B(2,n﹣1)关于x轴对称,则(m+n)2019的值为( )A、0 B、1 C、﹣1 D、320197. 下列运算正确的是( )A、 B、 C、 D、8. 如图,AD平分∠BAC,AB=AC,连接BD,CD并延长,分别交AC,AB于点F,E,则图中全等三角形共有( )
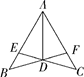 A、2对 B、3对 C、4对 D、5对9. 一艘轮船在静水中的最大航速为30千米/时,它沿江以最大航速顺流航行100千米所用时间,与以最大航速逆流航行60千米所用时间相等,江水的流速为多少?设江水的流速为 千米/时,则可列方程( )A、 B、 C、 D、10. 如图, 是 的角平分钱, ,垂足为 . 若 ,则 的度数为( )
A、2对 B、3对 C、4对 D、5对9. 一艘轮船在静水中的最大航速为30千米/时,它沿江以最大航速顺流航行100千米所用时间,与以最大航速逆流航行60千米所用时间相等,江水的流速为多少?设江水的流速为 千米/时,则可列方程( )A、 B、 C、 D、10. 如图, 是 的角平分钱, ,垂足为 . 若 ,则 的度数为( )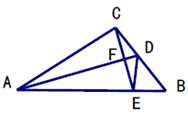 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
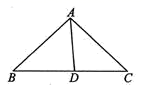
11. 一个正多边形的每个外角为60°,那么这个正多边形的内角和是。12. 已知 ,则 的值是.13. 目前我国芯片已可采用14纳米工艺.已知14纳米为0.000000014米,数据0.000000014用科学记数法表示为.14. 如图,在△ABC中,AB=AC,D为BC上一点,且CD=AD ,AB=BD,则∠B的度数为 .
 15. 若 中不含 的一次项,则 的值为16. 已知 是完全平方式,则 .17. 若分式方程 =a 无解,则a的值为.18. 已知a+ =3,则a2+ 的值是 .
15. 若 中不含 的一次项,则 的值为16. 已知 是完全平方式,则 .17. 若分式方程 =a 无解,则a的值为.18. 已知a+ =3,则a2+ 的值是 .三、解答题
-
19. 因式分解
(1)、﹣2a3+12a2﹣18a(2)、9a2(x﹣y)+4b2(y﹣x)20. 解分式方程:(1)、(2)、21. 先化简,再求值: ,其中 .22. 如图,在平面直角坐标系中, 的三个顶点分别为 .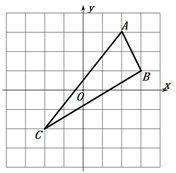 (1)、请在图中作出 关于 轴的对称图形 ( 的对称点分别是 ) ,并直接写出 的坐标;(2)、求 的面积23. 如图CE=CB,CD=CA,∠DCA=∠ECB,求证:DE=AB.
(1)、请在图中作出 关于 轴的对称图形 ( 的对称点分别是 ) ,并直接写出 的坐标;(2)、求 的面积23. 如图CE=CB,CD=CA,∠DCA=∠ECB,求证:DE=AB.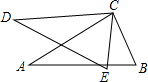 24. 已知a,b,c为三角形ABC的三边,且满足 ,试判断三角形ABC的形状.25. 在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且AE=BD,
24. 已知a,b,c为三角形ABC的三边,且满足 ,试判断三角形ABC的形状.25. 在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且AE=BD,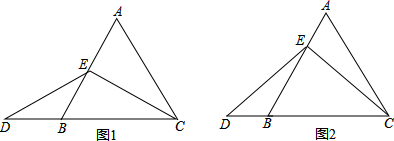 (1)、当点E为AB的中点时,如图1,求证:EC=ED;(2)、当点E不是AB的中点时,如图2,过点E作EF//BC,求证:△AEF是等边三角形;(3)、在第(2)小题的条件下,EC与ED还相等吗,请说明理由.
(1)、当点E为AB的中点时,如图1,求证:EC=ED;(2)、当点E不是AB的中点时,如图2,过点E作EF//BC,求证:△AEF是等边三角形;(3)、在第(2)小题的条件下,EC与ED还相等吗,请说明理由.