广西壮族自治区百色市德保县2020-2021学年八年级上学期数学期末考试试卷

试卷更新日期：2021-03-22 类型：期末考试

进入出卷网下载

一、单选题

1. 下列四个图案中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列各点中，位于第四象限内的点是（）

A、（-2，-3） B、（-1，0） C、（-1，4） D、（2，-3）

查看试题解析
3. 在△ABC中，AB＝5，AC＝8，则BC长可能是（）

A、3 B、8 C、13 D、14

查看试题解析
4. 函数 $y = \frac{x}{5 - x}$ 中自变量 $x$ 的取值范围是（）

A、 $x \neq 5$ B、 $x \geq 5$ C、 $x \leq 5$ D、 $x > 5$

查看试题解析
5. 一次函数 $y = - 3 x + m$ 的图象上有两点 $A (1, y_{1}) 、 B (3, y_{2})$ ，则 $y_{1}$ 与 $y_{2}$ 的大小关系是（）

A、 $y_{1} > y_{2}$ B、 $y_{1} < y_{2}$ C、 $y_{1} = y_{2}$ D、无法确定

查看试题解析
6. 下列语句中是真命题的是（）

A、同旁内角互补 B、三角形三条中线不会交于一点 C、到线段两个端点距离相等的点在线段的垂直平分线上 D、三角形按边分类可分为不等边三角形和等边三角形

查看试题解析
7. 如图，已知∠ABC=∠DCB，若再增加下列条件中的某一个，仍不能判定△ABC≌△DCB，则这个条件是（）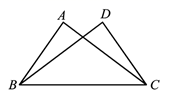

A、∠A=∠D B、AC=DB C、AB=DC D、∠ACB=∠DBC

查看试题解析
8. 关于函数 $y = x - 3$ ，下列说法正确的是（）

A、在 $y$ 轴上的截距是3 B、它不经过第四象限 C、当x≥3时，y≤0 D、图象向下平移4个单位长度得到 $y = x - 7$ 的图象

查看试题解析
9. 如图，△ABC≌△DEF，已知BC＝5cm，BF＝7cm，则EC长为（）

A、1cm B、2cm C、3cm D、4cm

查看试题解析
10. 在平面直角坐标系中，已知点A（a+2，2a-2）在y轴上，点B在第三象限，AB=2，且AB∥x轴，则点B的坐标是（）

A、（-2，-6） B、（-6，-2） C、（-2，-3） D、（-3，-2）

查看试题解析
11. 如图，若一次函数 $y_{1} = - x - 1$ 与 $y_{2} = a x - 3$ 的图象交于点 $P (m ， - 2)$ ，则关于 $x$ 的不等式： $- x - 1 > a x - 3$ 的解集是（）

A、 $x > 1$ B、 $x < 1$ C、 $x > 2$ D、 $x < 2$

查看试题解析
12. 如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点（1，1），第2次接着运动到点（2，0），第3次接着运动到点（3，2）……按这样的运动规律，经过第2021次运动后，动点P的坐标是（）

A、（2021，0） B、（2020，1） C、（2021，1） D、（2021，2）

查看试题解析

二、填空题

13. 已知等腰三角形两边的长分别为1cm，3cm，则该等腰三角形的周长为 $c m$ .

查看试题解析
14. 如图，已知∠B=∠D=90°，CB=CD，∠2=57°，则∠1=°.

查看试题解析
15. 已知，如图，在△ABC中，∠C=90°，AD平分∠BAC，CD=2cm，则点D到AB的距离为cm.

查看试题解析
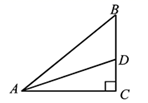16. 如图，已知点D是△ABC的边BC的中点，点E是边AC的中点，且△ABC的面积为20 $c m^{2}$ ，则△DEC的面积是 $c m^{2}$ .

查看试题解析
17. 如图，已知函数 $y = k x + b$ 与 $y = m x + n$ 的图象交于点 $P$ （1，2），那么关于 $x$ ， $y$ 的方程组 ${\begin{array}{l} y = k x + b \\ y = m x + n \end{array}$ 的解是.

查看试题解析
18. 如图，已知△ABC是等边三角形，AQ=PQ，PR=PS，PR⊥AB于点R，PS⊥AC于点S，有以下四个结论：①点P在∠BAC的平分线上；②△BRP≌△QSP；③QP∥AR；④△PQC是等边三角形，其中正确的有个.

查看试题解析

三、解答题

19. 已知，△ABC在平面直角坐标系中的位置如图所示.

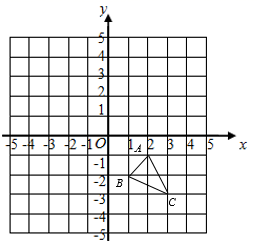
（ 1 ）将△ABC向上平移4个单位长度，再向左平移5个单位长度，画出平移后所得的△A₁B₁C₁ ，并写出C₁的坐标；

（ 2 ）画出△A₁B₁C₁关于 $x$ 轴对称的△A₂B₂C₂ ，并写出点B₂坐标_；

查看试题解析
20. 如图： $∠ A = 60 °$ ， $∠ A C E = 110 °$ ，求 $∠ A B D$ 的度数.

查看试题解析
21. 已知正比例函数 $y = k x$ 经过点（2，6）.

(1)、求 $y$ 与 $x$ 之间的函数表达式.

(2)、当 $y = - 3$ 时，求 $x$ 的值.

查看试题解析
22. 如图，已知点 $C$ 是 $A B$ 的中点， $C D$ ∥ $B E$ ，且 $C D = B E$ .

(1)、求证：△ACD≌△CBE.

(2)、若 $∠ A = 87 ° ， ∠ D = 32 °$ ，求∠B的度数.

查看试题解析
23. 如图，已知，在△ABC中， $∠ C = 90 °$ ，AB的垂直平分线DE交AC于点D，垂足为E，若∠A=30°，CD=4cm，求AC的长.

查看试题解析
24. 新冠肺炎肆虐全球，但病毒无情人有情，最美逆行者不顾个人安危奔赴疫情前线.某公司前往慰问医护人员，欲购进甲，乙两种呼吸机捐赠给医院.若购进甲、乙两种呼吸机共90台，甲种呼吸机每台单价4000元，乙种呼吸机每台单价比甲种少1000元.

(1)、求购买甲，乙两种呼吸机的总费用y元与甲种呼吸机台数x台之间的函数关系式.

(2)、若该公司购进甲种呼吸机台数不低于乙种台数的一半，则如何购买两种机器能使花费最少？最少费用为多少元？

查看试题解析
25. 如图，已知，在△ABC中，AB =AC，AD是BC边上的中线，AM是△ABC的外角∠CAE的平分线.

(1)、求证：AM∥BC；

(2)、若DN平分∠ADC交AM于点N，判断△ADN的形状并说明理由.

查看试题解析
26. 如图，已知直线 $l ： y = k x + b$ 与 $x$ 轴交于A（-3，0）、与 $y$ 轴交于B点，且经过（1，8），在 $y$ 轴上有一点C（0，3），动点D从点A以每秒1个单位的速度沿 $x$ 轴向右移动，设动点D的移动时间为 $t$ 秒.

(1)、求 $k$ 、 $b$ 的值；

(2)、当 $t$ 为何值时△COD≌△AOB，并求此时点D的坐标；

(3)、求△COD的面积S与动点D的移动时间 $t$ 之间的函数关系式.

查看试题解析